赛络纺加捻三角区内纤维的受力分析
2014-03-27徐伯俊刘新金
刘 娜, 徐伯俊, 刘新金
(江南大学 纺织服装学院, 江苏 无锡 214122)
赛络纺是一种新型的纺纱方式,它是由2根粗纱平行喂入细纱机双喇叭口,经牵伸系统在前罗拉钳口输出并复合,通过钢丝圈和锭子的加捻卷绕成纱[1]。由于赛络纺单股纱以及成纱均具有一定的捻度,类似于纱线合股,因此其具有表面光洁和耐磨性能良好等诸多优良性能。赛络纺成纱三角区类似于股线加捻三角区,三角区内单股纱受力以及纤维的受力分布情况较为复杂,因此,对赛络纱成纱三角区的研究也越来越多,一般使用的方法为理论计算和模拟,如余燕平[2]对Siro系列纺纱复合三角区的力学性能进行了研究,安降龙[3]研究了赛络纱三角区动态力学特征和非对称三角区的力学性能,刘新金等[4]通过研究赛络纱加捻三角区纤维的受力分析了赛络纱的扭矩,而利用有限元模拟的方法对赛络纱加捻三角区的研究还较少。
影响赛络纱三角区内纤维受力性能的因素众多,如纱线捻度、纱线中纤维细度、纱线线密度、锭速、钢丝圈型号等。由于纱线张力对成纱三角区的结构具有重要影响,三角区结构的改变导致三角区内纤维受力的变化,从而引起纤维在三角区内的转移发生改变,进而影响成纱性能,而纱线捻度、锭速以及钢丝圈型号对纱线张力的影响较为显著。基于此,本文利用不同的纱线捻度、锭速以及钢丝圈型号改变纺纱张力,采用有限元方法研究赛络纱三角区内纤维受力分布。
1 加捻三角区模型建立
1.1 加捻三角区几何模型
赛络纺纺纱过程中,2根须条同时从前罗拉前钳口输出,继而通过钢丝圈和锭子的加捻作用合股成纱,加捻三角模型如图1所示。图中:D为三角区的宽度;H为三角区高度;F为作用在加捻点O上的纺纱张力;α、β为单股纱与成纱三角区中心线的夹角,纺纱角α+β与纱线的捻度和纱线的直径有关,满足tan(α+β)=2πdT[5]。式中:d为纱线直径;T为纱线捻度。
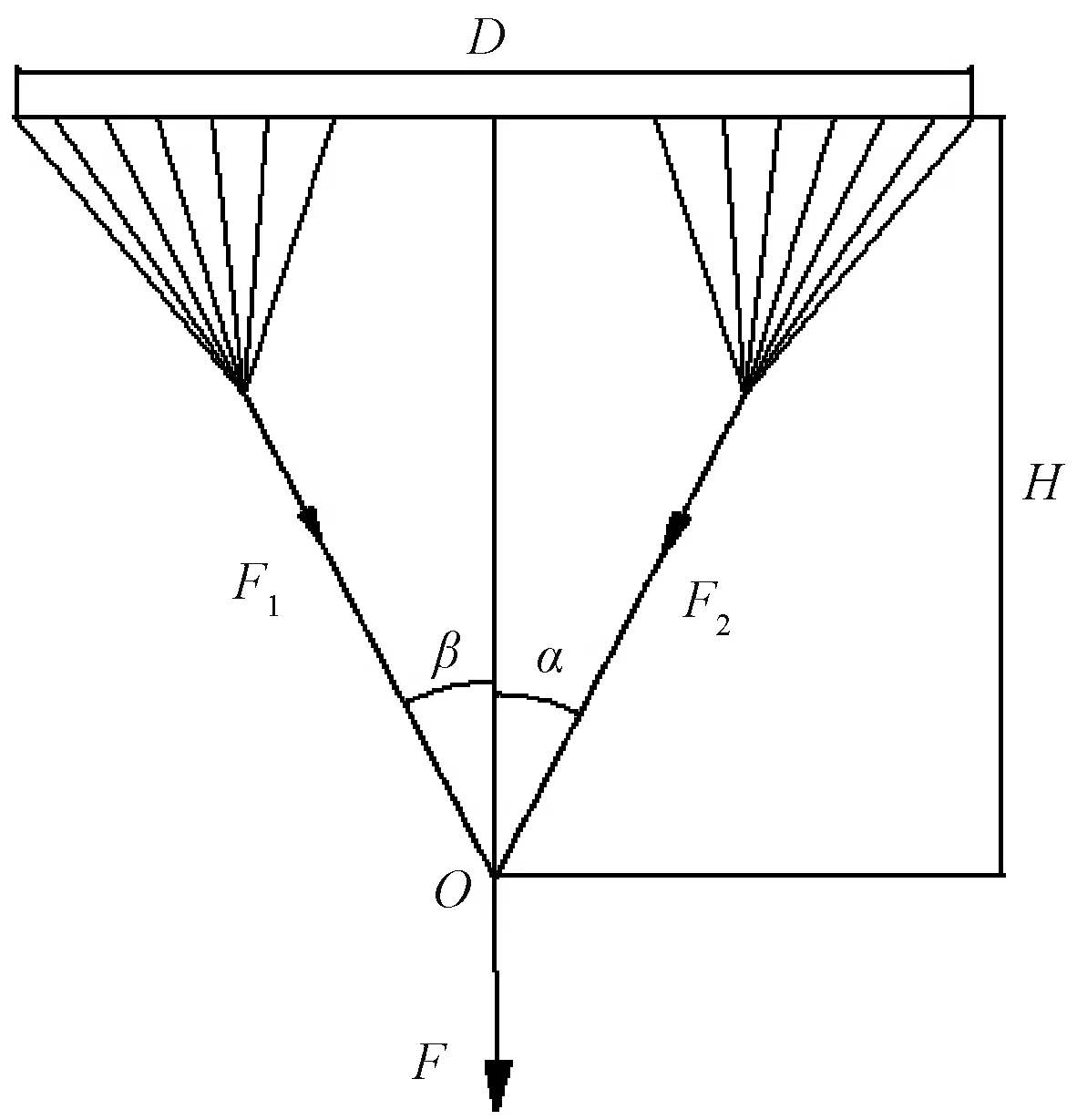
图1 赛络纱成纱三角区纤维几何模型Fig.1 Fibers geometry model in Sirospun spinning triangle
赛络纱单股纱成纱三角区纤维几何排列如图2所示。图中:θ表示第τ根纤维与垂直于前罗拉钳口线纤维之间的夹角;D1、D2为单股纱成纱三角的宽度;H1、H2为单股纱成纱三角的高度;F1、F2为单股纱成纱三角区的张力,其方向由纺纱角决定。

图2 左、右侧单股纱成纱三角纤维几何排列Fig.2 Fiber distribution at left (a) and right (b) yarn spinning triangle
1.2 模拟条件
假设纤维为具有弹性变形的细长圆柱体,纤维一端均匀排列并固定在前罗拉钳口线上,另一端汇聚成加捻点,纤维均匀分布在前罗拉钳口线与加捻点之间,纤维无重叠现象。垂直于前罗拉钳口线的纤维初始应变为零,分布在其两边的纤维初始应变根据θ计算得到,纤维在成纱三角区的坐标分布如图2所示。在模拟纤维受力时,不考虑纤维弯曲,纤维应力应变遵循胡克小变形原则,加捻三角区在被纺纱张力拉伸过程中,若纤维受到的拉力大于由初始应变产生的力,则纤维被继续拉长,若小于或等于,则纤维出现负伸长状态即被压缩状态或者保持伸长不变状态。
赛络纱成纱三角区中,左右两侧的单股纱成纱三角区关于三角区中心线对称分布,假设α=β,F1=F2,H1=H2,D1=D2,本文只对左侧单股纱成纱三角区内纤维受力进行分析。
以精梳棉18.2 tex赛络纱为例探讨赛络纱成纱三角区内纤维受力分布。其中,假设纤维线密度为0.15 tex,纤维弹性模量为5 N/tex,纱线横截面内纤维根数为128根。分别采用8 000、11 000、14 000 r/min 的锭速和6/0、4/0、5/0的钢丝圈进行纺纱实验。在湿度为50%,温度为32 ℃车间环境下进行纺纱,从空管始纺到纺至纱管长度的三分之一处的过程中,在钢领板上升阶段时测试纺纱张力F。测试纺纱张力仪器为YG2301轮式03120310-单纱张力计,利用该仪器沿纱线行进方向夹持住纺纱段处的纱线,并读取张力数值,每管纱测试20次,取其平均值得到该管的纺纱张力。测试结果如表1所示。另外,实际纺纱时,在前胶辊表面涂上少量滑石粉,纺纱完成后,利用直尺测量前胶辊长度方向上滑石粉脱落的宽度,得出单股纱加捻三角区的宽度(D1),然后根据β计算出单股纱加捻三角区的高度(H1)。文中只考虑捻系数对三角区几何结构的影响,不考虑钢丝圈质量以及锭速对其的影响作用。加捻三角区的几何参数见表2。

表1 纺纱张力Tab.1 Spinning force

表2 纺纱三角区的几何参数Tab.2 Spinning triangle parameters
1.3 有限元模型的建立
有限元方法是采用数学的方法模拟解决复杂的实际问题,有限元软件提供了接近实际的单元使其解决实际问题更为准确[6]。文中采用三维弹性梁单元进行线性结构静力分析模拟纤维在三角区内的受力。三维弹性梁单元力学性质和纤维力学特性十分接近,是拉、压、弯、扭的单轴线受力单元,在每个节点上具有6个自由度,X、Y、Z这3个方向的线位移,X、Y、Z这3个轴的角位移,选择适合弹性力学分析的矩阵分析法进行模拟分析[7]。该梁结构属于自然离散结构,其分析过程是将节点位移作为基本变量,先对梁单元进行分析,建立单元内力与位移之间的关系,然后再对梁结构进行整体分析。根据各节点的变形协调条件和静力平衡条件建立结构上的节点载荷和节点位移之间的关系,形成结构的总刚度矩阵和总刚度方程。解出各节点位移值后,再由单元内力与位移之间的关系求出梁结构的内力[8]。
根据上述的纺纱三角区的几何尺寸以及有限元提供的单元,建立如图3所示的赛络纺单股纱加捻三角区有限元模型。

图3 左侧单股纱加捻三角区有限元模型Fig.3 Finite element model of left single yarn spinning triangle
2 有限元分析结果
根据表1提供的参数,采用ANSYS有限元分析软件进行模拟分析,根据模拟条件设置弹性梁单元的初始应变,设置材料类型和材料属性,分析类型设置为线性静力分析,利用结果后处理器里的单元表功能提取纤维的张力。
2.1 纺纱张力对三角区内纤维受力的影响
根据表1中实验编号为1,2,3和4,5,6以及表2提供的参数进行有限元模拟,图4示出锭速与三角区内纤维张力分布之间的关系,图5示出钢丝圈型号与三角区内纤维张力分布之间的关系。其中,X轴方向表示纤维在三角区中的位置,左侧加捻三角区中最左侧的纤维定义为第1根纤维,Y轴方向表示纤维张力。由图4、5中的曲线图变化趋势可得知,加捻三角区的几何参数不同,三角区内纤维受力的分布也会有差别。由图4可知,当锭速从8 000 r/min增加至14 000 r/min时,三角区内纤维受到的最大拉伸力从0.717 cN增加至1.499 cN,最大压缩力由0.276 cN增加至0.776 cN。另外,由图4可知,随着锭速的增加,三角区内两侧相同位置的纤维受到的力有明显变大现象,但对位于三角区中部纤维的受力影响不大。如图5所示,采用4/0、5/0、6/0 3种不同质量钢丝圈进行纺纱时,三角区内纤维张力变化范围分别为1.041~-0.163 cN、0.956~-0.168 cN、0.914~-0.17 cN,变化量分别为1.204、1.124、1.084 cN。从上述分析易得,纺纱张力越大,三角区内最左侧纤维受力越大,且整个三角区内纤维受力变化量越大。

图4 锭速与三角区内纤维张力分布的关系Fig.4 Fiber tension distributions at left single yarn spinning triangle with different spindle speed

图5 钢丝圈型号和三角区内纤维张力分布的关系Fig.5 Fiber tension distributions at left single single yarn spinning triangle with different traveller
2.2 捻系数对三角区内纤维受力的影响
当细纱捻系数发生变化时,纺纱角度会随之改变,三角区的高度和宽度也会变化。根据表2提供的参数进行有限元分析,在相同的纺纱张力F为31.0 cN时,模拟不同纱线捻系数下三角区内纤维受力分布。图6示出捻系数和三角区内纤维受力分布之间的关系。由图中曲线可知,捻系数的变化对三角区内呈拉伸状态或压缩状态的纤维根数影响较大。捻系数为400、450、500时,三角区中承受压缩力的纤维根数分别为37、24、20根,其中当捻系数为400时,由于加捻三角区的高度和宽度均较大,在纺纱张力的作用下,三角区右侧的纤维受到的拉力不足以克服因初始应变产生的轴向力而呈现出负的轴向力状态,三角区内呈压缩状态的纤维根数较多,当捻系数增加时,三角区的高度与宽度均出现较小趋势,成纱三角区最左侧和最右侧的纤维受到的均是拉力作用,其中,捻系数为500时,三角区最右侧纤维受到的拉伸作用较为明显,右侧受到拉伸作用的纤维根数较多,并且纤维在三角区内受到的最大拉伸力与最大压缩力之间的差异最大。
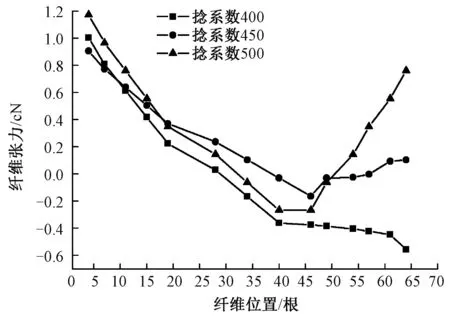
图6 捻系数和三角区内纤维张力分布的关系Fig.6 Fiber tension distributions at left single yarn spinning triangle with twist factor
2.3 结论分析
根据上述分析,若纺制中特纱精梳棉18.2 tex,采用捻系数为400时,捻系数相对较小,三角区内相同位置纤维受力较小且纤维受力差异较小,纤维在三角区内的转移幅度较小导致纱线内纤维的抱合力较小,为减少纺纱过程中纱线断头,适合采用较低纺纱张力,即选择较低的锭速,较轻的钢丝圈型号;采用捻系数为450和500时,捻系数相对较大,纱体内纤维之间的抱合力大,纺纱过程中不易断头,适合采用较高的纺纱张力,大的纺纱张力使三角区内不同纤维的受力差异较大,转移幅度大,在纱体内形成自锁结构的可能性增加,有利于提高纱线强力,减少纱线毛羽。
3 实验分析
3.1 实验条件
本文实验选用FA507B型细纱机纺制精梳棉18.2 tex赛络纱,粗纱定量为4.0 g/10 m,细纱捻系数分别为400、450、500,前区牵伸加带压力棒的3.0隔距块,加压方式为螺旋弹簧摇架加压,钢丝圈为4/0,喇叭口间距为2.1 mm,纺纱速度分别为8 000、11 000、14 000 r/min。捻系数为450时,采用4/0、5/0、6/0 这3种不同的钢丝圈进行纺纱实验。
3.2 成纱强力与毛羽分析
选用YG063全自动单纱强力仪测试纱线的拉伸性能,测试温度为20 ℃,湿度为65%,测试试样用每种实验方案纱管数为3,每管测试10次,设置预加张力为9.1 cN,试样夹持长度为0.5 m,采用等速拉伸方式进行拉伸实验。采用YG172A型纱线毛羽测试仪测试纱线毛羽,测试速度为30 m/min,每管测试长度为100 m。通过测试得到断裂强力、断裂伸长率和断裂强度、不同长度的纱线毛羽根数,结果如表3所示。

表3 纱线强力与毛羽Tab.3 Yarn strength and yarn hairiness
纺纱张力、锭速以及捻系数、钢领、钢丝圈的变化对纱线性能有着重要的影响[9-11]。若只考虑锭速变化对纱线强力、毛羽的影响效果,由表3可得,纱线捻系数为400时,纱线强力在锭速为11 000 r/min时最大,断裂强力变异系数较小,有害毛羽的数量也较小。由图4模拟分析结果可看出,当锭速为11 000 r/min时,三角区内纤维受力较锭速为8 000 r/min时的纤维受控制性较好,纤维不易滑脱,三角区左右侧的纤维张力差异较大,纤维之间会产生较强的相互转移和包缠而且纤维不易因受力过大而断裂形成有害毛羽,而且纤维强力的利用率较高,且在纱线受到外界拉伸力时,纤维不易相互滑移,有利于纱线强力的增加。当锭速达到14 000 r/min时,纤维在三角区内以及三角区左右两侧的纤维受力差异较大,纤维可能发生断裂形成毛羽或飞花,一定长度内纱线截面内的根数会有很大的差别,减少了纱截面内的纤维根数,纱线发生细节现象,降低了纱线强力,增大了纱线强力的变异系数。
若在同一锭速和捻系数条件下,选择不同的钢丝圈进行实验纺纱。由表3可见,钢丝圈选择较重时,纱线的强力及断裂伸长率较大,但同一批次的纱中纱线的强力变异系数较大,钢丝圈过重或过轻均会引起有害毛羽的增加。由图5给出的模拟结果可知,3种钢丝圈下纤维受力在三角区内的分布趋势是一致的,但钢丝圈偏重时,纤维受力较大,纤维之间的相互作用力增加,有利于纱线强力。选择较重的钢丝圈,三角区内纤维受力及纤维相互作用增加,可能会使纤维发生断裂形成毛羽,但若钢丝圈过轻,纤维在三角区内的相互作用较弱,纤维之间的相互控制力减少,部分纤维易不受控制而散落在纱体表面形成毛羽。
由表3可知,若在其他条件相同时,选择不同的捻系数进行纺纱实验,纱线强力及断裂伸长随之增大,但有害毛羽会增加。由表2可知不同捻系数下加捻三角区的几何形态会有很大差别。由图6所示的模拟结果分析可知,捻系数增大时三角区内左右两侧处于拉伸状态的纤维根数会增加,左右两侧的纤维同时控制位于三角区中间的纤维,纤维间相互转移幅度及频率增加,纤维之间的抱合能力增加,呈独立状态的纤维数量减少,纤维之间的相互滑移减少,纱线的强力会提高,但在其转移过程中,部分纤维也可能发生断裂或被挤出纱体形成毛羽。若三角区内纤维受力过小,纤维之间的相互控制力较小,三角区内纤维呈独立状态的根数增加,纤维在三角区内易滑脱致使其头端浮于纱体表面形成毛羽。
4 结 论
通过有限元模拟结果分析和实验验证可得知:赛络纱单股纱成纱三角区几何形态对三角区内纤维受力大小以及分布有着重要作用,当三角区的高度减小时,三角区内处于压缩状态的纤维根数具有明显减少趋势。三角区几何形态一定时,当纺纱张力增加时,纤维张力在三角区内的分布规律不变,但纤维张力会呈增大趋势,纤维张力的变化范围也逐渐增大。
纺纱过程中,其他条件一定时,钢丝圈、锭速和捻系数这3种因素中,锭速对纺纱张力和成纱三角区的纤维受力影响作用最为显著。
本文结合上述有限元模拟结果分析和实际的纺纱实验,对纱线性能进行了定性分析,经分析可知,三角区内纤维受力大小以及其在三角区内的分布对纱线性能影响作用显著。
FZXB
[1] 谢春萍,徐伯俊.新型纺纱[M].北京: 中国纺织出版社, 2009: 131-140.
XIE Chunping, XU Bojun. New Spinning [M]. Beijing: China Textile & Apparel Press, 2009: 131-140.
[2] 余燕平. Siro系列纺纱复合三角区力学分析及其成纱性能研究[D]. 上海: 东华大学, 2005: 10-29.
YU Yanping. Study on performance and mechanic analysis of compound triangle area for siro-series spinning technology [D]. Shanghai: Donghua University, 2005: 10-29.
[3] 安降龙. 赛络纺复合成纱机理、纱线结构及其力学性能研究[D]. 上海: 东华大学, 2009: 21-41.
AN Xianglong. Study on the mechanism structural and mechanical performance of sirospun composite yarn [D]. Shangjai: Donghua University, 2009: 21-41.
[4] LIU Xinjin, SU Xuzhong. Research on sirospun yarn torque using airflow false twisting device[J].Journal of the Textile Institute, 2013, 104(5): 473-480.
[5] LI Shengyan, XU Bingang, TAO Xiaoming, et al. Numerical analysis of the mechanical behavior of a ring-spinning triangle using the finite element method [J]. Textile Research Journal, 2011, 81(9): 959-971.
[6] 张红松, 胡仁喜, 康士廷. ANSYS13.0有限元分析从入门到精通[M]. 北京:机械工业出版社,2011:
1-20.
ZHANG Hongsong, HU Renxi, KANG Shiting. ANSYS13.0 Mechanical And Structural Finite Element Analysis From Beginning To The Proficiency[M]. Beijing: China Machine Press, 2011: 1-20.
[7] 王新敏,李义强,许宏伟. ANSYS结构分析单元与应用[M].北京:人民交通出版社,2011: 89-90.
WANG Xinmin, LI Yiqiang, XU Hongwei. Structural Analysis Unit and Application[M]. Beijing: China Communications Press, 2011: 89-90.
[8] 刘伟, 高维成, 于广斌. ANSYS12.0宝典[M].北京: 电子工业出版社, 2010: 166-255.
LIU Wei, GAO Weicheng, YU Guangbin. ANSYS12.0 Dictionary[M].Beijing: Publishing House of Electronics Industry, 2010: 166-255.
[9] 周光茜,郝凤鸣.纺纱张力控制技术的研究[J].棉纺织技术,2002,30(1): 25-27.
ZHOU Guangqian, HAO Fengming. The research on the technology of spinning force[J]. Cotton Textile Technology, 2002 ,30(1): 25-27.
[10] 刘妍,刘士广,姜华强. 细纱捻系数与纱线强力的相关性分析[J]. 棉纺织技术, 2008,36(8): 15-18.
LIU Yan, LIU Shiguang, JIANG Huaqiang. Relativity analyses of yarn twist factor and yarn strength[J].Cotton Textile Technology, 2008 ,36(8): 15-18.
[11] 陈玉峰. 赛络纺纱钢领、钢丝圈的选配实践[J].纺织器材, 2010,37(6):27-29.
CHEN Yufeng. The optional practice on the ring and traveler of Sirospun spinning[J].Textile Accessories, 2010, 37(6):27-29.
