“主题词教学法”在课堂教学中运用的效果分析——以“n阶行列式”的课堂教学为例

成 乐，张晓军，杨树生

（河套学院 理学系，内蒙古 巴彦淖尔 015000）

成 乐，张晓军，杨树生

（河套学院 理学系，内蒙古 巴彦淖尔 015000）

本文以《线性代数》[1]中“n阶行列式”的课堂教学为例，对在实际课堂教学中运用“主题词教学法”[2]的效果进行了研究与分析，并给出了由“主题词教学法”的运用而获得的教育教学绩效.

1 引言

“主题词教学法”是由河套学院张晓军、杨树生教授在总结多年教学经验的基础上于2011年提出的一种创新性（原创性）教学法[2].通过多年（2007年至今）的教学实践与研究证明，“主题词教学法”具有良好的可操作性与实效性，并适合于不同层次和不同类型课程的教学.主题词教学法的核心要点是在讲授新课之前先展示本节课的主题词，包括本节课的重要知识点、蕴含的思想方法和思维方式与技巧、能体现课程美与方法美及提升综合素养与综合能力等的关键词，三部分主题词用分号隔开.教学过程的运行按照主题词的顺序循序渐进并始终与教学内容融会贯通.

行列式是线性代数中最基本的概念，是解决线性方程组问题的最重要工具之一.学生对行列式概念掌握的程度直接影响学习线性代数课程的效果，而行列式的概念又是学生在学习线性代数时遇到的第一个较为抽象并与之前接触过的代数对象完全无关的概念，如何很好地引导学生深刻理解行列式的概念是教学的重点，也是难点.自2011年以来，通过尝试在教学中使用“主题词教学法”进行教学，学生在记忆、理解、掌握基本知识方面有了一个系统的、清晰的认识；在把握课程内容所蕴含的思想方法和思维方式与技巧方面提升了理论认识的高度；在审美方面获得了由课程带来的美的体验，提升了审美能力，提高了综合素养与综合能力，获得了非常好的效果.

下面以《线性代数》中“n阶行列式”的课堂教学为例，对在实际课堂教学中运用“主题词教学法”的效果进行研究与分析.

2 教学过程

2.1 展示主题词（一般写在黑板的最上方一行或用课件展示）

在引入本节课的题目之后，先复习回顾二阶、三阶行列式的概念及对角线法则，接着展示本节课主题词：①余子式，代数余子式，展开式，n阶行列式；②观察与联想，类比，推广，转化与化归，抽象，殊途同归；③简洁美，统一美，技巧美.其中①给出了本节课的重要知识点，实现知识与技能目标；②给出了本节课内容中所蕴含的数学思想与方法，实现能力目标；③给出了本节课中体现的数学之美，实现情感、态度与价值观目标.

2.2 按照知识主题词的顺序循序渐进展开课堂教学，并有意识引导学生理解、体会、感悟教学内容中蕴含的数学思想方法、思维方式与分析问题和解决问题的技巧，引导学生体会、感悟课程美和方法美，实现提升学生综合素养与综合能力的目标.

2.2.1 推导三阶与二阶行列式的关系，引入余子式的概念（主题词：余子式；观察与联想、转化与化归）.

通过对三阶行列式的算式进行重新整理，将其与二阶行列式建立关系，让学生通过观察和联想，引导启发学生探索二阶行列式与其前面元素的关系，从而引出余子式的概念:

定义1 在三阶行列式

中，把元素aij(i=1,2,3;j=1,2,3)所在的第i行与第j列划去，剩下的元素保持原来的相对位置不变构成的二阶行列式称为元素aij的余子式，记作Mij.

2.2.2 引入代数余子式的概念，统一形式（主题词：代数余子式，展开式；观察与联想，转化与化归，简洁美，统一美）.

给出了余子式的概念之后，将三阶与二阶行列式的关系式进行改写，此时，余子式前面的符号有正有负，为了统一其形式，进一步引导学生发现其正负号与元素行标、列标的密切关系，进而引出代数余子式的概念.

定义2设Mij是aij的余子式，令Aij=(-)1+jMij，称Aij为元素aij的代数余子式.

至此，已将三阶与二阶行列式的关系式进一步简化，得到三阶行列式按照第一行元素展开的展开式，并提示学生注意三阶行列式的计算最终转化为二阶行列式的计算：

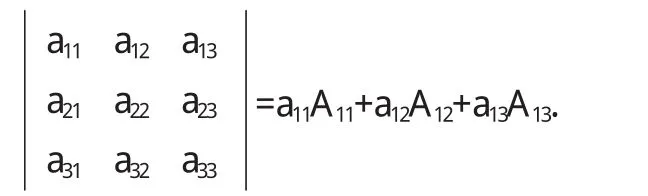
2.2.3 进一步引导学生通过观察三阶行列式的定义式，并仿照上述做法得到三阶行列式按照第二、三行元素展开的展开式（主题词：展开式；类比，观察与联想；统一美）.

2.2.4 进一步引导学生给出n阶行列式的定义（主题词：n阶行列式；类比，推广，抽象）.

类比二阶与三阶行列式，引导学生写出四阶行列式及一般的n阶行列式；类比三阶行列式的余子式及代数余子式，引导学生抽象出n阶行列式余子式及代数余子式的概念；类比三阶与二阶行列式之间的关系，引导学生抽象出一般n阶行列式与n-1阶行列式之间的关系，给出n阶行列式的定义.

定义3由n2个数aij(i,j=1,2,…,n)组成的n阶行列式记作：D=

当n=1时，D=|a11|=a11；

2.2.5 引导学生体会数学的方法与技巧之美（主题词：观察与联想，殊途同归；简洁美，技巧美）.

教学过程中可以通过例子展示利用不同方法解决同一问题（殊途同归）的难易程度与繁简度的差别，从而让学生体会数学的方法与技巧之美，使学生获得由课程带来的美的体验，提升审美能力，提高综合素养.

解 （方法一）按照第一或三行展开（略）.

（方法二）按照第二行展开（简洁美，技巧美）.

3 教学评价与效果分析

2013年7月，通过问卷的形式（课程结束以后，学生都要填写“线性代数课程学习总结[3]”）对“主题词教学法”的使用效果进行了评价分析，结果表明，在线性代数的教学过程中，通过使用“主题词教学法”，取得了较好的教育教学绩效.

3.1 学生评价及效果与分析

在85名学生中，97%的学生认为“主题词教学法”是一种实用的、美妙的并使人感觉课堂学习比较轻松而目标明确的教学方法；96%学生认为“主题词教学法”能够有利于自己把握重点、归纳总结，对课下复习有很大帮助；65%的同学认为自己的思考能力、自学能力得到了提高，学到了转化、类比、化简等数学思想方法和技巧；有76%的学生表示提高了对数学的学习兴趣；62%的学生表示逻辑思维、抽象思维、推理能力得到锻炼和提高；58%的学生表示，审美能力也有了提高.

3.2 教师评价及效果与分析

通过“主题词教学法”的使用，教师的教学技能、对教材的把握等都有很大提高，教学效果显著（主要表现为学生对课程的学习兴趣与积极性有明显提高）.

任课教师认为：“主题词教学法”的使用对教师提出了较高的要求，首先教师必须对教学内容的重点、教学内容中蕴含的数学思想与方法、处理问题的技巧以及体现的数学美等有非常准确的把握，这就要求教师在备课上狠下功夫，要认真挖掘教学内容的内涵.其次要在授课过程中能够按照主题词循序渐进、突出重点、自然衔接、融会贯通，并让学生真正能体会到数学的内在美，从而不断增加对数学的兴趣，激发对知识的渴望与探求，提高学生解决问题与创新的能力.

〔1〕杨树生,张晓军.线性代数[M].北京：北京邮电大学出版社，2010.21-26.

〔2〕张晓军,杨树生.“主题词”教学法[J].新天地(高校论坛), 2011（12）.

〔3〕张永胜,等.信息环境下多元学与教的方式有效融入日常教学的研究 [M].呼和浩特：内蒙古人民出版社，2010.143-148.

〔4〕同济大学数学系.线性代数[M].上海：同济大学出版社，2010.1-17.

〔5〕张顺燕.数学的思想、方法和应用[M].北京：北京大学出版社，2009.45-65.

〔6〕于秀林，任雪松.统计分析学[M].北京：中国统计出版社，2006.98-115.

教学法”在课堂教学中运用的效果分析
——以“n阶行列式”的课堂教学为例

G642

A

1673-260X（2014）02-0166-02

内蒙古自治区高等教育科学研究“十二五”规划立项课题（NGJGH 2013062）

教学法；运用；效果