奇异p(x)-Laplace方程正解的存在性
2014-03-27张晓丽
赤峰学院学报·自然科学版 2014年3期
张晓丽
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
奇异p(x)-Laplace方程正解的存在性
张晓丽
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文讨论了奇异p(x)-Laplace方程正解的存在性.
奇异p(x)-Laplace方程;正解;存在性
本文将研究如下的奇异p(x)-Laplace方程Dirichlet问题
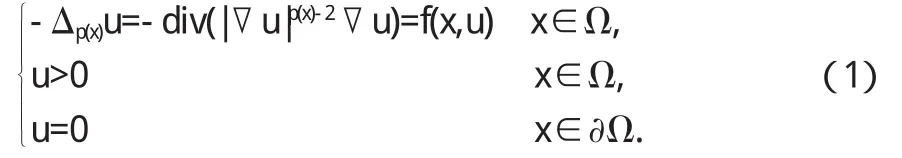
这里Ω是RN上的一有界C2域,N≥3,p∈C+1(Ω),算子Δp(x)u=div(|▽u|p(x)-2▽u)是所谓的p(x)-Laplace算子,f是Ω× (0,+∞)上的Caratheodory函数,满足
(A1)a0(x)≤f(x,t)≤a1(x)t-γ(x),(x,t)∈Ω×(0,t0),这里a0(x),a1(x)是可测函数,并且a1(x)≥a0(x)>0,γ(x)>0,t0>0,γ(x)∈C(Ω).
注 满足上述条件的f(x,t)在t=0点可能出现奇性.
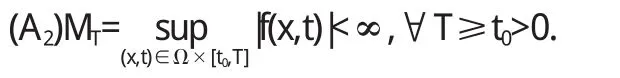
除上述两个条件外,本文主要结果还用到假设
(A3)存在一属于的非负函数φ满足(Ω),其中r(x) (A4)|f(x,t)|≤Ctr(x)-1,t≥t0,r(x) 本文的主要结果 定理1如果(A1)和(A3)成立,问题(1)在空间W1,p(x)(Ω)中存在一个上解并且假设 (ⅰ)(A2)成立并且u∈L∞(Ω),或(ⅱ)(A4)成立, O175.25 A 1673-260X(2014)02-0003-01

