面向目标靶区的双程波动方程地震定向照明分析

雷 涛,顾汉明,李 列,李添才,方中于,蔡志成,余信江

(1.中国地质大学(武汉)地球物理与空间信息学院,湖北武汉430074;2.中国地质大学构造与油气资源教育部重点实验室,湖北武汉430074;3.中海石油(中国)有限公司湛江分公司,广东湛江524057;4.中海油能源发展股份有限公司工程技术物探技术研究所,广东湛江524057)

近年来,地震照明分析技术的发展为复杂地区的观测系统优化设计提供了可靠的依据。常见的地震照明分析方法主要分为两大类：基于射线理论的射线照明分析[1-2]和基于波动理论的波动方程照明分析[3-5]。射线照明分析主要提供打击次数分析、模拟偏移振幅分析、方位角分析等信息,具有计算速度快、不受模型边界条件的限制、支持模型部分缺失情况下的正演计算等优点。但是,射线追踪采用高频近似理论,存在射线盲区,只适用于速度横向变化不大的简单模型[6]。波动方程照明分析对速度模型没有任何限制,尤其是在复杂模型成像研究方面具有较高的计算精度,能够较为真实地反映地震波在地下介质传播过程中的能量分布,为合理地优化设计观测系统提供可靠的依据。

根据照明度计算方法的不同,波动方程照明度又分为总照明度和定向照明度[7-8],总照明度是地下介质振动的总能量,可以反映每个质点对震源或者检波器的能量响应;而定向照明度是地下介质振动沿各个不同方向的分解,可以反映每个质点在特定方向上的能量分布,据此可以计算不同入射角和反射角组合的角域照明响应。

近几年来,Chen等[9]、冯伟等[10]、陈凌[11]、Wu等[12-13]基于波动方程的波场外推算子和Garbor-Daubechies(G-D)框架的小波束局部波场分解理论,实现局部平面波分解,得到空间和方向都具有局部性的局部平面波小波束,应用于观测系统定向照明分析和采集倾角响应分析以及定向化偏移成像。陈生昌等[14-15]提出波动方程双程地下方向照明方法,同时从观测系统的震源位置和检波器位置计算地震波在地下传播过程中分布在不同方向上的能量。以上两种方法均以单程波波动方程为基础,若介质参数随深度方向变化,则上行波和下行波存在耦合关系[16],利用单程波算子计算的照明度更多地反映透射波的能量,丢失了层间反射、多次波以及绕射波等信息,与实际地震波传播规律不符,尤其在复杂介质区域,计算的照明度误差更大。但是,基于单程波算子的计算速度明显优于双程波算子。裴正林[17]基于地震波能量理论,通过波印廷矢量的波场方向性分解计算出震源定向照明度和源-检组合定向照明度。该方法虽然采用了双程波动方程,但是根据直达波场计算的定向照明量没有包含反射波的信息。同时,该方法与单程波方法类似,没有考虑质点在整个时间尺度上的传播方向会发生改变,所以略显不足。

我们采用双程声波波动方程传播算子[18],在每一时刻根据地震波传播的波印廷矢量对每个质点的波场值进行方向性分解,然后将整个时间尺度上不同方向的波场值分别进行能量叠加,进而计算每个质点不同方向上的能量分布,最终计算出地震波定向照明度。正演计算时采用交错网格差分格式以及PML边界条件[19]。

1 波场方向性分解

根据弹性波理论[20],弹性介质能流密度可用应力张量和位移分量(或速度)表示,关系式如下：

(1)

式中：Ei为能流密度分量;σij为应力张量;ui为位移分量;vi为速度分量。(1)式也称为波印廷矢量,其中能流密度表示单位时间内通过与它垂直的单位截面积的机械能。根据(1)式可知,已知应力张量和速度分量,就可以计算地震波的能流密度矢量和能量传播方向。

实际勘探生产中多应用纵波信息,若只考虑纵波成分,则弹性波方程弱化为声波方程,声波的能流密度矢量可表示为

(2)

根据(2)式,已知声波波场压力P和速度分量vi,就可以计算声波的能流密度和能量传播方向。

对于各向同性弹性介质,能流密度矢量的方向和波传播方向一致[21-22],因此,只要确定波在每一质点的能流密度矢量各个分量的值,就可以确定能流密度矢量的方向,进而确定该点地震波的传播方向。所以,我们选择不同的角度进行角度域滤波,从而实现波场的方向性分解,即

(3)

式中:F(x,z,θ)为二维定向滤波器,一般取余弦窗函数；θ为波的传播角度(或入射角)。

2 地震定向照明度

根据入射波的能量和方向,第i个点源在二维模型空间点(x,z)处的定向照明度[23]可定义为

(4)

对于源总定向照明度、源-检定向照明度以及源-检组合总定向照明度的定义等内容详见文献[24],由于篇幅限制,本文不再赘述。定向照明不仅能分析地震波的角度域照明分布,而且能提供倾角域地震响应和反射角域地震响应。

3 数值模型试验

为了验证本文方法的正确性和可行性,设计了透镜体模型、层状介质模型和盐丘模型进行数值试验,针对不同目标靶区作定向照明分析。

3.1 透镜体模型

图1和图2是对高、低速透镜体模型分别计算出的源总照明度和源总定向照明度。模型大小均为4000m×2000m,高速透镜体的速度为4000m/s,低速透镜体的速度为1000m/s,背景速度为2000m/s。

图1 高速透镜体模型定向照明分析(红色代表照明度高,蓝色代表照明度低,下同)a 总照明度; b 25°～35°照明度; c 40°～50°照明度; d -5°～5°照明度; e -25°～-35°照明度; f -40°～-50°照明度

图2 低速透镜体模型定向照明分析a 总照明度; b 25°～35°照明度; c 40°～50°照明度; d -5°～5°照明度; e -25°～-35°照明度; f -40°～-50°照明度

网格大小为Δx=Δz=5m,时间采样间隔为Δt=0.5ms,炮点范围为500～3500m,炮点间隔为10m,共301炮。震源为雷克子波,主频为20Hz。

从图1和图2可以看出：

1) 定向照明清晰地反映了震源照明的方向特性;

2) 透镜体对地震波照明能量的分布规律以及照明方向有着明显影响;

3) 高速透镜体的源总定向照明度可以明显改善透镜体之下远端的照明量(相对于源总照明度而言),对近端的照明量没有改善,而低速透镜体则与之相反;

4) 高速透镜体对其下的介质具有能量屏蔽作用,而低速透镜体对其下的介质具有能量聚焦作用(图1a,图2a)。

3.2 水平层状介质模型

图3和图4分别是水平层状介质模型及其单炮总照明度和定向照明度。模型大小为7000m×4000m,网格大小为Δx=Δz=10m,时间采样间隔为Δt=1ms,炮点范围为500～6500m,炮点间隔为20m,共301炮。震源类型同透镜体模型。

从图4可以看出：

图3 水平层状介质模型

1) 水平层状介质对地震波的照明方向以及强度的分布有着明显的影响;

2) 透射波的能量明显高于反射波的能量(图4c红色椭圆圈内所示);

3) 对于同一个界面上同一个炮点,不同的入射角度对应不同的反射段,由此可以推断,对于某一个反射段,选择不同的入射角可以追踪到不同的炮点位置,并从中优选出特定角度的最佳激发范围,具体见图5和图6。

图5反映了总照明量和定向照明量随炮点位置的变化规律：对于水平层状模型,总照明量在目标区的正上方达到最大值;随着入射角的增大,方向照明在目标区达到最大值的位置逐渐发生偏移,且定向照明量逐渐减小。图6反映了不同入射角的定向照明量在目标区达到最大值的最佳炮点位置与图5中的不同能量曲线峰值位置对应:0°照明对应炮号S115;30°照明对应炮号S70;45°照明对应炮号S47;60°照明对应炮号S24。

图4 水平层状介质模型定向照明分析a 总照明度; b 25°～35°照明度; c 40°～50°照明度; d -5°～5°照明度; e -25°～-35°照明度; f -40°～-50°照明度

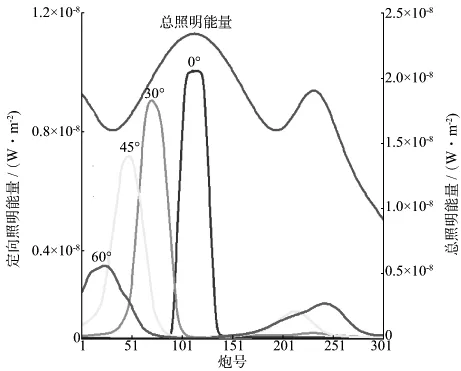
图5 水平层状模型不同炮点的总照明以及定向照明在目标区(图6黑框所示)的能量分布曲线

图6 水平层状模型不同入射角的最佳炮点定向照明

3.3 盐丘模型

由于高速岩体的屏蔽作用,盐丘之下的成像效果一般较差。为了验证定向照明分析的有效性,选择横向起伏较大的深水层状模型,如图7所示,分析不同组合照明对盐下目标区域(图7黑框内)照明效果的改善。模型大小为6000m×4000m,炮点范围为500～5500m,共251炮,网格大小为Δx=Δz=10m,时间采样间隔为Δt=1ms,炮点间隔20m。震源类型同透镜体模型。

图7 盐丘模型

图8为对盐丘模型计算出的总照明度和定向照明度。从图8a可以看出,能量主要集中在海水层,由于盐丘的屏蔽作用,位于盐下的目标区域总照明度较弱,存在照明阴影区。从图8b至图8e可知,在目标区域的0°方向地震波对目标区域的贡献极小,说明在目标区域很难产生0°方向的地震波场;当入射角增加到30°左右时,目标区域的能量骤增,且能量主要来自于透过盐丘的透射能量;当入射角增加到45°～60°时,能量强度和均匀性逐渐减弱,这主要是由上覆速度体以及盐丘形态等因素造成的。推断可知,在盐丘的左上方小角度(30°左右)范围内,目标区域对炮集的响应较好。从图8e 至图8h可知,当入射角反向增加到-30°左右时,目标区域的能量增加较快,其主要来自目标区域上方的低速地层而非高速盐丘体;当入射角增加到-45°左右时,目标区域的能量和均匀性高于海水层,且高于其它方向的方向照明效果;当入射角增加到-60°左右时,由于入射角较大、目标区域较深等原因,到达的能量很弱。

图8 盐丘模型定向照明分析a 总照明度; b 25°～35°照明度; c 40°～50°照明度; d 55°～65°照明度; e -5°～5°照明度; f -25°～-35°照明度; g -40°～-50°照明度; h -55°～-65°照明度

图9为盐丘模型不同炮点的总照明以及定向照明在目标区域的能量分布曲线,据此可以更好地分析单炮的总照明和各方向照明对目标区域的贡献。对于总照明而言,1～190号炮点的总照明量变化不大,且维持在一个较低的水平;190～235号炮点的总照明量增加较快;235～251号炮点的总照明量有所下降,这主要是由于偏移距较大造成的。若选取最大能量的70%作为阈值,则选择合理的激发范围为炮号222～251,即x方向4920～5500m。对于各个方向照明而言,不同的炮点范围所对应的方向照明的最佳角度范围是不同的：在10～30号炮点范围内,总照明主要来自60°左右的方向照明;在50～70号炮点范围内,总照明主要来自45°左右的方向照明;在100～115号炮点范围内,总照明主要来自30°左右的方向照明;在170～185号炮点范围内,0°方向的照明量较小,由于方向照明的窗口采用的是±5°,推断可知此范围内炮集的总能量主要来自-5°～-25°以及5°～25°范围内的方向照明；而190～235号炮点的总照明量增加较快的原因主要是来自-25°～-50°范围内的方向照明贡献大。

图9 盐丘模型不同炮点的总照明以及定向照明在目标区域的能量分布曲线

综上所述,若选取总能量最大值的70%作为阈值,则合理的激发范围为x方向4920～5500m,在此范围内可以对炮点进行加密,且采用右边放炮的方式有利于盐下目标的成像;在不同的炮点范围内,各个角度的方向照明的贡献值不同,-45°左右的方向照明对总照明的贡献最大,而0°方向的贡献最小,同时,由于盐丘的形态等因素影响,0°方向的贡献范围偏离目标区域的正上方(炮号125附近)。在上述最佳激发范围内选择最佳的角度激发，将得到最佳的效果。

4 结束语

本文提出的双程声波方程定向照明技术通过波印廷矢量对波场值进行方向性分解,可以快速地分析目标靶区照明量主要来源的方位以及炮点的分布范围,从而为地震采集设计中炮点加密以及检波器的参数选择提供依据;同时,角度域的定向照明可以很好地反映构造倾角响应,为观测系统评价提供可靠的量化信息。但是,我们提出的定向照明技术适用于二维,还有很多地方需要完善,并有待推广到三维模型,以更好地服务于石油勘探开发。

参 考 文 献

[1] Muerdter D,Kelly M,Ratcliff D.Understanding subsalt illumination through ray-trace modeling:part 1—simple 2D salt models[J].The Leading Edge,2001,20(6)：578-594

[2] Muerdter D,Kelly M,Ratcliff D.Understanding subsalt illumination through ray-trace modeling:part 2—dipping salt bodies,salt peaks,and nonreciprocity of subsalt amplitude response[J].The Leading Edge,2001,20(7):688-687

[3] Xie X B,Jin S W,Wu R S.Wave-equation-based seismic illumination analysis[J].Geophysics,2006,71(5):169-177

[4] Xie X B,Jin S W,Wu R S.Three-dimensional illumination analysis using wave-equation based propagator[J]:Expanded Abstracts of 73rdAnnual Internat SEG Mtg,2003,989-992

[5] 董良国,吴晓丰,唐海忠,等.逆掩推覆构造的地震波照明与观测系统优化[J].石油物探,2006,45(1)：40-47

Dong L G,Wu X F,Tang H Z,et al.Seismic wave illumination for overthrust nappe structures and optional seismic survey design[J].Geophysical Prospecting for Petroleum,2006,45(1):40-47

[6] Hoffmann J.Illumination resolution and image quality of PP- and PS-waves for survey planning[J].The Leading Edge,2001,20(9):1008-1014

[7] Ostmo S,Maao F.Seismic illumination from finite difference modeling[J].Expanded Abstracts of 65thEAGE Conference & Technical Exhibition,2003,146

[8] Wu R S,Chen L.Mapping directional illumination and acquisition—aperture effiency by beamlet propagators[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002,1352-1355

[9] Chen L,Wu R S,Chen Y.Target-oriented beamlet migration based on Gabor-Daubechies frame decomposition[J].Geophysics,2006,71(2):37-52

[10] 冯伟,吴如山,马在田.单向传播子的局部平面波分解以及在定向照明分析和目标特征成像中的应用[J].地球物理学进展,2007,22(1)：171-178

Feng W,Wu R S,Ma Z T.Local plane wave decomposition of one-way propagator and the applications to directional illumination analysis and target structure oriented imaging[J].Progress in Geophysics,2007,22(1):171-178

[11] 陈凌.小波束域波场的分解、传播及在地震偏移成像中的应用[D].北京：中国地震局地球物理研究所,2002

Chen L.Beamlet-domain wavefield decomposition,propagation and its applications in seismic migration/imaging[D].Beijing:Institute of Geophysics,China Seismological Bureau,2002

[12] Wu R S,Chen L,Xie X B,et al.Directional illumination and acquisition dip-response[J].Expanded Abstracts of 65thEAGE Conference and Technical Exhibition,2003,147

[13] Wu R S,Chen L.Directional illumination analysis using beamlet decomposition and propagation[J].Geophysics,2006,71(4):147-159

[14] 陈生昌,马在田,吴如山.波动方程双程地下方向照明分析[J].同济大学学报(自然科学版),2007,35(5)：681-685

Chen S C,Ma Z T,Wu R S.Two-way subsurface directional illumination analysis by wave equation[J].Journal of Tongji University(Natural Science),2007,35(5)：681-685

[15] 陈生昌,毕亚杰,林晨.地震观测系统评价的波动方程方向照明方法[J].石油地球物理勘探,2009,44(6):656-661

Chen S C,Bi Y J,Lin C.Seismic acquisition geometry evaluation method based on wave equation directional illumination technique[J].Oil Geophysical Prospecting,2009,44(6):656-661

[16] 皮红梅.双程波动方程数值模拟和照明分析方法研究[D].吉林：吉林大学,2002

Pi H M.Method research on two-way wave-equation forward modeling and illumination analysis[D].Jilin:Jilin University,2002

[17] 裴正林.波动方程地震定向照明分析[J].石油地球物理勘探,2008,43(6):645-651

Pei Z L.Analysis on wave equation seismic directional illumination[J].Oil Geophysical Prospecting,2008,43(6):645-651

[18] 陈可洋.完全匹配层吸收边界条件研究[J].石油物探,2010,49(5):472- 477

Chen K Y.Study on perfectly matched layer absorbing boundary condition[J].Geophysical Prospecting for Petroleum,2010,49(5):472-477

[19] 陈可洋.声波完全匹配层吸收边界条件的改进算法[J].石油物探,2009,48(1):76-79

Chen K Y.Improved algorithm for absorbing boundary condition of acoustic perfectly matched layer[J].Geophysical Prospecting for Petroleum,2009,48(1):76-79

[20] 杜世通.地震波动力学理论与方法[M].山东东营：中国石油大学出版社,2009:25-27

Du S T.Seismic waves dynamics theory and methods[J].Shandong Dongying:China University of Petroleum Press,2009:25-27

[21] 牛滨华.半空间介质与地震波传播[M].北京：石油工业出版社,2002:56-68

Niu B H.Half-space medium and seismic wave propagation[M].Beijing:Petroleum Industry Press,2002:56-68

[22] 崔兴福,张关泉.地震波方程人工边界的两种处理方法[J].石油物探,2003,42(4):452-455

Cui X F,Zhang G Q.Two processing methods for artificial boundary of seismic wave equation[J].Geophysical Prospecting for Petroleum,2003,42(4):452-455

[23] Luo M,Cao J,Xie X B,et al.Comparison of illumination analysis using one-way and full wave propagators[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,67-70

[24] 李万万.基于波动方程正演的地震观测系统设计[J].石油地球物理勘探,2008,43(2):134-141

Li W W.Design of seismic geometry based on wave equation forward simulation[J].Oil Geophysical Prospecting,2008,43(2):134-141