一种有效的三维PS波保幅叠前时间偏移方法

黄中玉,王于静

(中国石油化工股份有限公司石油勘探开发研究院,北京100083)

振幅随偏移距的变化(即AVO或AVA和AVP)受震源子波、反射与透射以及几何扩散的影响。只有消除这些影响,AVO异常才能用于检测含油气信息。Kirchhoff偏移算法是在绕射叠加中应用不同的加权函数来消除反射振幅受到的上述影响的。Newman[1]在绕射叠加偏移/反演中尝试结合振幅信息,为真振幅偏移研究奠定了理论基础。Bleistein等[2-3]基于Born反演理论,采用射线理论和WKBJ(Wentzel-Kramers-Brillouin-Jeffery )的格林函数,推导出2.5D真振幅偏移加权函数。Cerveny等[4]把Beylkin行列式和向量联系起来,用动力学射线追踪计算Beylkin行列式。Schleicher等[5]提出用旁轴射线理论计算加权函数,使给出的加权函数具有明显的物理意义。为了克服计算格林函数耗时和占存储资源多的缺陷,Joe等[6]在背景速度为常数的假设条件下,导出一种高效2.5D真振幅偏移加权函数表达式。Sun等[7]基于Schleicher的基本理论,通过假设射线段为直线的条件,导出3D真振幅加权函数,并将该方法推广到PS波资料的偏移处理。Zhang等[8]在Kirchhoff偏移方法研究中讨论了精确和近似加权函数,给出了常速介质和变速介质条件下各种维数的加权公式。Hugh[9]在Kirchhoff叠前PSTM保幅加权研究中,给出了等效偏移距(EOM)叠前PSTM算子。针对各向异性介质,Vanelle等[10]研究了基于旅行时的真振幅偏移方法。徐升等[11]在复杂介质保真振幅Kirchhoff深度偏移方法研究中提出了多值走时情况下多次偏移算子的高效重构3D叠前深度偏移快速算法。孙建国[12]在Kirchhoff型真振幅偏移和反偏移方法研究中提出孔径有限的保幅偏移算法。李振春等[13]对Kirchhoff和波动方程两类偏移方法的真振幅偏移算法进行了综述。黄中玉等[14]、张丽艳等[15-16]对PS波PSTM技术作了介绍和综述,后者在相对振幅保持的PS波PSTM方法研究中做出了探索性研究。

我们基于Bleistein的基本理论[2-3]和Joe的高效真振幅加权函数[6],推导出适合共炮点保幅偏移的2.5D振幅加权函数表达式,同时基于Schleicher理论[5]和Sun近似方法[7],给出3D保幅加权函数,该函数描述了震源子波、反射以及几何扩散的影响。通过对Bleistein和Schleicher两种类型加权函数以及相应的共炮点、共检波点和零偏移距加权函数进行分析对比,确定了一种3D PS波保幅各向异性PSTM的实用方法。

1 方法原理

1.1 Bleistein类型加权函数

Bleistein类型的加权函数是将利用射线理论和WKBJ的格林函数推导出的Kirchhoff叠前偏移公式用Beylkin行列式来表示[17]。在背景速度为常数的特殊条件下,共炮点反演算子β的积分表达式为

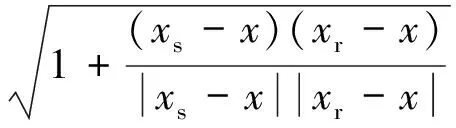
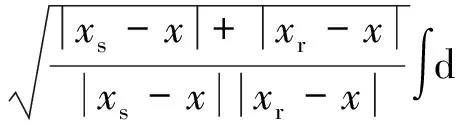
exp[-iω(xs-x+xr-x)/c]D(ω,ξ)

(1)

其加权函数可表示为

(2)

式中：xs=(xs,0)是震源位置,xr=(xr,0)为检波点位置,x=(x,z)为成像点位置；c是纵波背景速度；F为高通滤波器；D为地震道的傅里叶变换。

根据向量公式我们有：

(3)

式中：θ是射线路径xsxxr的夹角。假设背景速度为常数,利用速度和时间的关系,公式(2)就可以写为：

(4)

再利用余弦定理、三角函数关系以及炮间距2h导出：

(5)

将(5)式代入(4)式就得到高效2.5D共炮点振幅加权函数表达式：

(6)

Joe等[6]给出的高效2.5D共偏移距振幅加权函数的表达式为：

(7)

(6)式与(7)式的形式相似,差异仅在于最后一项表达式。Joe等[6]给出的零偏移距振幅加权函数表达式为

(8)

将深度域转换到时间域,速度c用PS波等效速度vc代替,旅行时t用tc代替,就能够用于PS波时间域的相对振幅保持的PSTM处理。

1.2 Schleicher类型加权函数

Schleicher积分偏移方法与其它算法的不同之处是它采用了零阶射线理论(即描述一次反射波的旅行时和振幅),避免了Born近似带来的问题,在弹性介质中可以直接用于保持振幅的偏移,其振幅加权函数是采用稳相法对叠加积分进行渐进估算得到的。考虑平滑弹性介质,Schleicher给出积分偏移的加权函数一般形式为

(9)

式中：αs,αg分别是炮点和检波点处的射线入射角和出射角；vs是震源点的纵波速度；Γs,Γg分别是描述矢量ξ与炮点和检波点位置的关系矩阵,由观测系统决定；Nsr,Ngr分别为旅行时二阶混合导数组成的Hessian矩阵。绕射叠加积分中考虑了沿射线路径存在的焦散问题,k1,k2是沿射线路径的焦散数。对于不同观测系统,该加权函数可以演变出适合于共偏移距、共炮点、共中心点和零偏移距的多种形式。

假设炮点到成像点、成像点到检波点的射线段为直线段,(9)式就可以演变为一种适合共偏移距的3D加权函数：

(10)

式中：tr,ts和tg分别为成像点的时间、成像点到炮点的时间以及成像点到检波点的时间；vr为成像点的RMS速度；H是炮检距；L是成像点在地面投影与炮检中点的连线距离；α是上述连线与炮检线间的夹角。公式(10)依次描述了震源子波、反射和几何扩散的影响。

研究表明,射线入射角和出射角不仅与观测系统有关,还与速度模型有关。公式(10)基于直射线假设,用于大偏移距数据计算加权函数时会产生较大的误差。因此,我们利用更精确的弯曲射线旅行时公式计算αs,αg：

(11)

式中：炮点和检波点的旅行时可以用弯曲射线旅行时来替代,其一般形式为

(12)

式中：ci(i=1,2,3)是与层速度有关的系数；k为偏移距高阶项近似的等效常数；xs和xg分别为对应反射点到炮点和检波点的距离。直射线和弯曲射线旅行时公式在时距曲线上分别呈现双曲线和非双曲线的特征。对于远偏移距,弯曲射线计算的走时远小于直射线走时[18]。相对直射线方法,弯曲射线方法对于PSTM处理效果有明显改善,在成像道集(CIP)和PSTM叠加剖面中均有所表现。图1给出了转换波各向异性PSTM直射线和弯曲射线方法在CIP道集上应用的结果。图1a为直射线3D PS波各向异性PSTM处理的CIP道集,可见CIP道集中反射同相轴逐渐上翘,远偏移距道集出现明显的过偏现象(见图1a中矩形框)。图1b 则是弯曲射线3D PS波各向异性PSTM处理的CIP道集,可见弯曲射线算法对于远道过偏的现象有明显的校正拉平作用。

1.3 振幅加权函数的确定

上述振幅加权函数公式经过时深转换就可以演变为PS波PSTM的真振幅加权函数,因此我们可以利用这些公式进行3D PS波振幅加权函数空间分布规律的研究。以西部A区块三维转换波实际资料为例,在已知纵波和横波速度场的情况下,计算成像点道集(CIP为450)在某一成像时间点(3480ms)的振幅加权系数,并将振幅加权函数系数的分布用时间切片的方式显示(图2)。图2中白色圆点表示成像点,红色代表振幅加权系数值大。图2a为该工区3D3C观测系统示意图,图中红色表示CDP面元叠加次数高。图2b为公式(6)计算的2.5D共炮点振幅加权系数分布图,从图中可以明显看出,振幅加权系数在平面上分布不均匀,没有规律性。图2c为公式(8)计算的零偏振幅加权系数分布图,振幅加权系数分布规律与观测系统的覆盖次数分布趋势一致,但在CIP位置附近,平面上加权系数分布不均匀。图2d和图2e分别为公式(7)和公式(10)计算的2.5D和3D共偏移距振幅加权系数分布图,两者分布规律相似。

图1 三维PS波各向异性PSTM成像道集(CIP)a 直射线走时计算方法; b 弯曲射线走时计算方法

从振幅加权函数系数在平面上分布的均匀性以及与数据观测系统分布的一致性考虑,我们认为公式(7)与公式(10)作为加权函数较为合适。在理论上也是采用共偏移距的加权函数比共炮点和零偏移距的加权函数更合理,3D比2.5D的加权函数更合理。故确定公式(10)作为3D PS波真振幅偏移的加权函数。

图2 成像点上不同振幅加权函数系数平面分布(西部A区块)a 3D3C观测系统; b 2.5D共炮点; c 零偏移距; d 2.5D共偏移距; e 3D共偏移距

2 实际资料处理效果分析

应用上述4种振幅加权函数公式对西部A区块实际3D3C资料进行PS波弯曲射线保幅各向异性PSTM处理效果对比,图3显示了不同保幅加权函数处理的CIP道集(CIP为450),其中图3a 是没有应用加权函数处理的CIP道集,其对大偏移距的远道处理表现出过加权效果[6]。图3b至图3e 分别是用公式(6)、公式(8)、公式(7)和公式(10),即2.5D共炮点、零偏移距、2.5D共偏移距和3D共偏移距加权函数进行保幅处理的CIP道集。从图3方框中可以明显看出,图3b和图3c对大偏移距远道的处理也出现过加权现象,与无加权函数处理的效果相近(见图3a方框内)。图3d和图3e振幅加权效果相近,其振幅随偏移距的变化更加符合AVO规律。

图4显示了不同保幅加权函数处理的剖面效果对比(局部)。从图4中椭圆和矩形区域可以明显看出,应用共炮点加权函数(图4a)和零偏移距加权函数(图4b)出现了较强的偏移噪声,而共偏移距加权函数(图4c和图4d)的偏移噪声明显减弱,能量聚焦性有所改善,且后者偏移效果略好于前者。但3D共偏移距比2.5D共偏移距耗时多(近2倍),在权衡处理效果和计算耗时方面,可根据计算机能力选取最佳加权函数的处理方案。在并行或GPU高端计算机技术的支持下,选择公式(10)作为3D PS波各向异性PSTM加权函数是可行的。

图5为西部B区块3D PS波PSTM剖面的对比图(局部),其中图5a是直射线非保幅转换波PSTM剖面,图5b是采用弯曲射线3D共偏移距加权函数进行的保幅PSTM剖面。相比之下,图5b 所示成像剖面表现出偏移归位准确、断点清晰、薄层分辨率高等特点。

图3 西部A区块三维PS波PSTM处理的CIP道集对比a 无加权函数; b 2.5D共炮点加权函数; c 零偏移距加权函数; d 2.5D共偏移距加权函数; e 3D共偏移距加权函数

图4 西部A区块三维PS波PSTM处理的剖面对比(局部)a 2.5D共炮点; b 零偏移距; c 2.5D共偏移距; d 3D共偏移距

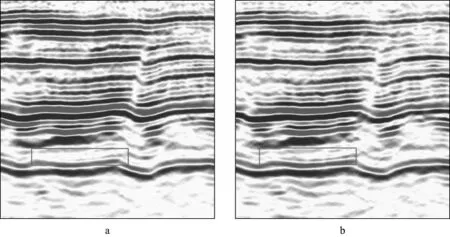
图5 西部B区块3D PS波PSTM处理的剖面对比(局部)a 直射线非保幅PSTM; b 弯曲射线保幅PSTM

3 结束语

对以Born近似或者Kirchhoff近似理论为基础的共炮点(共检波点)、共偏移距(或等效偏移距)和叠后加权函数类型,通过加权函数系数分布、CIP道集以及西部A,B两个区块3D PS波各向异性PSTM剖面分析,证实了共偏移距类型的3D振幅加权函数更适合3D PS波真振幅PSTM处理,能够降低3D PSTM剖面噪声,增强反射能量聚焦,有效改善转换波各向异性PSTM处理的效果,为后续转换波AVO分析和反演,纵波与转换波AVO联合反演提供相对保幅的叠前资料。

参 考 文 献

[1] Newman P.Amplitude and phase properties of a digital migration process[J].First Break,1990,8,397-403

[2] Bleistein N,Cohen J K,Hagin F G.Two and one-half dimensional Born inversion with an arbitrary reference[J].Geophysics,1987,52(1):26-36

[3] Bleistein N.On the imaging of reflectors in the earth[J].Geophysics,1987,52(7):931-942

[4] Cerveny V,de Castro M A.Application of dynamic ray tracing in the 3-D inversion of seismic reflection data[J].Geophysical Journal International,1993,173(7):776-779

[5] Schleicher J,Tygel M,Hubral P.3-D true-amplitude finite offset migration[J].Geophysics,1993,58(8):1112-1126

[6] Joe A D,Samuel H G,Gary E M,et al.Efficient 2.5D true-amplitude migration[J].Geophysics,2000,65(3):943-950

[7] Sun C W,Martinez R D.3D Kirchhoff PS-wave prestack time migration for V(z) and VTI media[J].Expanded Abstracts of 73rdAnnual Internat SEG Mtg,2003,957-960

[8] Zhang Y,Gray S,Young G.Exact and approximate weights for Kirchhoff migration[J].Expanded Abstracts of 70thAnnual Internat SEG Mtg,2000,1036-1039

[9] Hugh D G.Amplitude-preserving weights for Kirchhoff prestack time migration[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002,1212-1215

[10] Vanelle C,Sprinner M,Hertweck T,et al.Travetime-based true-amplitude migration[J].Geophysics,2006,71(6):S251-S259

[11] 徐升,Gilles Lambare.复杂介质下保真振幅Kirchhoff深度偏移[J].地球物理学报,2006,49(5):1431-1444

Xu S,Gilles L.True amplitude Kirchhoff prestack depth migration in complex media[J].Chinese Journal of Geophysics[J].2006,49(5):1431-1444

[12] 孙建国.Kirchhoff型真振幅偏移与反偏移[J].勘探地球物理进展,2005,25(6):1-5

Sun J G.Kirchhoff-type true-amplitude migration and demigration[J].Progress in Exploration Geophysics,2005,25(6):1-5

[13] 李振春,朱绪峰.韩文功.真振幅偏移方法综述[J].勘探地球物理进展,2008,31(1):10-16

Li Z C,Zhu X F,Han W G.Overview of true amplitude migration methods[J].Progress in Exploration Geophysics,2008,31(1):10-16

[14] 黄中玉,朱海龙.转换波叠前偏移技术新进展[J].勘探地球物理进展,2003,26(3):167-171

Huang Z Y,Zhu H L.New progress in converted wave prestack migration technology[J].Exploration Geophysics,2003,26(3):167-171

[15] 张丽艳,刘洋.转换波叠前时间偏移方法综述[J].地球物理学进展,2005,20(4)：1134-1139

Zhang L Y,Liu Y.Overview of prestack time migration for converted wave[J].Progress in Geophysics,2005,20(4)：1134-1139

[16] 张丽艳,刘洋,陈小宏.基于虚拟偏移距方法的转换波保幅叠前偏移[J].中国石油大学学报(自然科学版),2009,33(5):50-55

Zhang L Y,Liu Y.Overview of prestack time migration for converted wave[J].Progress in Geophysics,2005,20(4)：1134-1139

[17] Beylkin G.Imaging of discontinuities in the inverse scattering problem by inversion of a generalized Radon transform[J].Journal of Mathematical Physics,1985,26(1):99-108

[18] 黄中玉,曲寿利,王于静,等.层状各向异性介质转换波克希霍夫叠前时间偏移[J].地球物理学报,2009,52(12):3109-3115

Huang Z Y,Qu S L,Wang Y J,et al.Kirchhoff prestack time migration of PS-wave data for the layered anisotropic medium[J].Chinese Journal of Geophysics,2009,52(12):3109-3115