叠前反演数据优化处理技术

许自龙,孟繁举，唐 勇，宋 林，夏洪瑞

(1.中国石油化工股份有限公司石油物探技术研究院，江苏南京211103;2.大庆钻探工程公司地球物理勘探一公司研究院，黑龙江大庆163357;3.北京金阳普泰石油技术股份有限公司，北京100107;4.中国石油化工集团公司石油工程地球物理有限公司江汉分公司物探研究中心，湖北潜江433100)

叠前反演能够得到比叠后反演更准确的弹性参数，可提高储层预测尤其是流体预测精度，因而逐步成为储层预测的关键技术。在生产实践中，叠前反演已逐步成为地震资料解释性处理的常规环节。叠前反演主要分为叠前AVO反演、叠前弹性反演和叠前地震全波形反演。目前，反演技术的发展仍以修正和完善各种反演算法为主，众多专家学者提出了许多卓有成效的反演算法并在实践中取得了较好的效果[1-7]。当然，叠前反演的准确性不仅取决于反演算法，也取决于参与反演数据的品质。对于叠前反演所用地震数据品质的改善问题，已有一些地球物理工作者进行了有益的尝试并取得了成功的经验[8-12]，但实际生产中目前大都仍然采用常规处理的流程和技术。

叠前反演是在CMP道集的单道记录上进行，这种处理失去了叠加技术这个最强有力去噪技术的支撑，因而对参与叠前反演的数据品质有更高的要求。在常规处理流程中，一切以求出可供解释的偏移结果为主要目的，较少涉及为地震储层描述而进行保持反射波动力学特征的处理。另外，由于预处理之后的地震数据中存有的剩余时差和残余噪声大都可由偏移来消除，故在常规处理流程中，对由采集因素产生的误差及由处理流程、处理技术及不当参数而产生的处理误差有相当的容许度。而对上述误差，叠前反演算法对叠前反演数据不可能有偏移算法对偏移数据那样的容许度。这是因为叠前反演处理应用的数据是单道记录，这些单道记录没有经过保真处理，也没有经过叠加过程去除上述各种误差，因而没有满足叠前反演严格的应用条件，其将给叠前反演结果带来非常大的陷阱。

由于偏移速度不可能准确提供，偏移公式自身也仅仅是地震波传播规律的近似，因此经偏移后CRP道集中的有效信号不可能严格排齐。这样的数据不能完全满足AVO反演的应用前提(道集内的反射同相轴为水平)，由此而得到的反演结果会带有一些错误信息。

噪声是与有效信号如影随行的干扰信息，地震资料处理中的所有处理技术都涉及如何尽可能地减少噪声对有效信号的影响。遗憾的是，目前仍没有一种去噪技术能实现真正的信噪分离。更为严重地是，目前噪声消除几乎全部采用多道识别多道消除的思路，经这种去噪思路去噪处理后的记录不可避免地存有拟合噪声。即只要应用了多道消除思想，其一定利用相邻道的信息，处理记录的动力学特征必然会受到破坏。这样的记录应用于叠前反演，结果的真实性难以保证。

在地震数据采集和预处理过程中，CMP道集中的记录存有的振幅、相位误差，这些误差同样影响叠前反演结果。

综上所述，常规处理后的地震数据不能直接应用于叠前反演，而需应用新的技术对叠前反演数据进行叠前反演预处理，以满足叠前反演的需要。叠前反演数据优化处理的内容主要包括吸收补偿，频率、相位校正，剩余时差校正和去噪处理等。我们仅针对剩余时差校正及随机噪声消除(高保真去噪)问题展开讨论。

1 叠前反演数据的优化处理

1.1 基于常规多项式拟合的剩余时差校正技术

目前进行剩余时差校正的办法通常为速度调整和静校正方法，这两种方法均在一定程度上减少剩余时差，使信号同相轴相对排齐，但也都存有一定的缺陷。由于现行的动校/偏移算法均无法完全准确描述地震波的运动规律，其速度调整只是相对概念，不可能将同一道集内的有效信息完全排齐。静校方法采用的是单道整体移动，而叠前反演数据存在的剩余时差是由动校、静校及其它因素而产生，每道中不同时刻的有效信息存有时变性的剩余时差，用静校方法实施之后会产生顾此失彼的应用效果。

实现剩余时差校正的关键因素有二：①每道所接收信息的正确位置;②如何将有效信息校正到正确位置。我们知道，单道信息自身无法确定信息位置是否正确，只能靠多道来识别。由叠加原理知，叠加结果可相对准确地消除剩余时差。因而，对叠前反演CRP道集中每道记录而言，将某一CRP道集中每道记录分别与对应的叠加道分时窗互相关，可求出各道记录中每个时窗的剩余时差，然后采用滤波插值，即可消除各道记录中每一时刻的剩余时差[13]。

上述技术在建立模型道时采用线性拟合技术，而地震有效信息并非呈线性，由此建立的模型道并不能准确描述地震道信息的正确位置，因而需采用更为精确的算法来建立模型道。常规多项式拟合技术[14]是用曲线来拟合地震有效信息以达到消除噪声的技术，借用其用曲线拟合地震有效信息的思想来建立模型道，便可克服文献[13]中用直线拟合建立模型道存在的不足。另外，文献[13]中采用分时窗求时差，并用拉伸/压缩(滤波插值技术)消除时差，这种方法仅考虑了时窗内的整体效果，故不能使信号同相轴真正排齐;同时，拉伸/压缩技术将改变信号的波形特征。为克服这些缺陷，我们采用分波形求时差，然后采用静态时移方法消除时差。

以下以二维资料为例(三维资料则为二维拟合的扩展)进行分析。

1.1.1 常规多项式拟合建立模型道

为求取准确的叠加道以校正剩余时差，首先将叠前反演CRP道集叠加。因有些叠加道也存有误差，应对叠加道进行校正，才能得到更为准确的模型道。

根据文献[14]，对k叠加道上的i时刻tk,i(0)，应用常规多项式拟合公式，通过计算相邻叠加道上参与拟合的时刻tk,i(x)，可拟合出经过校正的叠加模型道。这种方法既消除了叠加道自身的误差，又增强了相邻道之间的连续性。常规多项式拟合公式为

(1)

式中：tk,i(x)为道相对号为x关于第k道时刻i的拟合时间值(以样点数表示);x为相邻道关于第k道的相对位置,x=-X,-X+1,…,-1,0,1,…,X-1,X(其中X为拟合记录道的一半);c1和c2为一次多项式和二次多项式系数;tk,i(0)为第k道时刻i拟合时，0表示拟合时的中心道，即第k道在所有拟合道的相对道号;k=1,2,…,N(其中N为某CRP道集中的总道数);i=1,2,…,L(其中L为单道样点数)。

通过扫描方式，可求得(1)式中的c1，c2，进而求出相邻各叠加道参与拟合的时间tk,i(x)，继而可拟合出模型道。

文献[14]基于去噪处理而提出，对参与拟合的数据采用中值约束下的矢量分解技术能够很好地达到这一目的。实施过程中，在需向中值矢量的垂直向量作投影时，不可避免地保留部分噪声。我们仅用常规多项式拟合的思想建立模型道，且仅以模型道为标准，确定对应道集内所有记录道上有效信息的正确位置。对此，叠加结果较中值约束下的矢量分解结果更具有代表意义。

在这里采用叠加方式生成叠加模型道：

(2)

式中：S(tk,i)为叠加模型道;s(tk,i(x))为在叠加道x时刻tk,i(x)的样点值;其它同(1)式。

1.1.2 分波形求取剩余时差及静态校正

在文献[13]中，对波形位置的校正采用分时窗的办法实施。即对模型道和道集中记录进行分时窗处理，应用互相关原理求取两者的时差，再应用拉伸/压缩的办法消除时差。这样处理将导致以下缺点：

1) 消除时差是以时窗为整体，并不能严格校平道集内每道记录的有效信息。

2) 应用拉伸/压缩处理，将改变记录原有频率和相位特征，给反演带来不利因素。

为此，将分时窗处理改为分波形处理。为此定义：每道记录中两次过零点的部分称之为一个波形。时差校正以每个波形为单位进行。于是有分波形求时差公式为

(3)

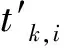
设在模型道上满足式(3)的波形为S(tk,ii),ii∈(1,I1)，若以下(4)式成立

(4)

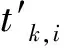
为避免采用拉伸/压缩方法产生波形形变，本文采用静态时移的方法消除时差。

1.2 基于横向滑动的时空变小波阈值保真去噪

目前，地震资料去噪技术大都采用多道识别、多道消除的技术思路。它利用相邻道的信息来识别噪声,并应用相邻道信息修正欲处理道信息。应用这类技术后，增强相邻道相似性，但去噪结果包含了相邻道信息而损失各道自身个性，信号的保真性降低。多项式拟合、中值滤波、RNA(随机噪声衰减)、F-X反褶积等均属于这类方法。在常规处理中，叠前去噪后的数据还要经过叠加/偏移处理，故可不需特别关注道集内各道自身个性。但叠前反演正是应用这些个性进行反演，因此，叠前反演前数据的去噪处理亟需单道保真去噪技术。

地震资料处理中的单道去噪技术包括带通滤波、时频峰值滤波及小波阈值等去噪技术。由于地震噪声和有效信号在同频带上共存，带通滤波的去噪能力有限;时频峰值滤波因应用魏格纳一维利分布(Winger-Ville Distribution,WVD)产生交叉项的影响,去噪效果不佳;而小波阈值去噪受控于阈值的准确性。鉴于目前没有新的单道信噪分离算法，多道识别、单道消除技术成为目前实现保真去噪的一种选择。

作为单道去噪技术的小波阈值去噪，其技术思路是对小波变换后小波系数(大的小波系数通常为信号，小的小波系数通常为噪声)计算阈值进行噪声消除。实践表明，仅采用单道技术很难求准所需阈值。基于此，在文献[15]中采用多道计算阈值、单道消除噪声的方法进行了相关叠加前的可控震源记录噪声消除。

在实践中，常用的小波变换阈值去噪公式为：

(5)

方差为该小波系数与标准值的差的平方。实践中，由于标准值难以求取，常取最小尺度下的小波系数的均值作为方差应用。而地震资料噪声具有时空变性质，这种以噪声均值为方差的方法十分粗糙，易产生过扼杀或过保留现象。文献[15]提出的时空变阈值去噪技术能够在相关叠加前的可控震源数据上应用并获得成功，源于它利用相关叠加前可控震源资料具有水平排齐、多道同幅同相的特点。文献[15]将相关叠加前的整个可控震源道集内所有记录叠加，并以叠加结果作为标准值，进而求取方差，使阈值求取不准的问题得到改善。

但是，用于叠前反演的CMP道集通常有几十甚至数百道，在整个道集内各道记录的振幅、频宽、相位均存有很大变化，CMP道集难以具有水平排齐、多道同幅同相的共性。因此，对于参与叠前反演的CMP道集而言，直接应用文献[15]的方法不可能求准时空变小波阈值。然而，在按偏移距选排的整个CRP道集内，相邻道记录之间近似持有上述共性，可采用局部相邻道叠加的方法来取代整个道集叠加，进而求取时空变阈值。具体做法为：以某一道为中心，取其左右各N道组成一子道集，在子道集上实现时空变阈值去噪;然后横向滑动一道，再进行相同的计算，直到整个CMP道集。由此，将文献[15]的方法改进为以下方法。

设σj,i(t)为在第j层尺度下，第i道时刻t的小波系数wj,i(t)的方差，则

(6)

式中：rj(t)是某道集在第j尺度下时刻t的数学期望(标准值);wj,i(t)为道集中的第j层尺度下第i道时刻t的小波系数。可取相邻若干道的叠加结果，特别地还可利用加权叠加结果作为数学期望rj(t)，其权用方差的倒数取代，则某道集第j层尺度下时刻t的数学期望(标准值)可表示为：

(7)

式中，2N+1为第i道相邻两边的求和道数。显然，若方差求取准确，就可求得准确可靠的加权叠加结果。反之，若叠加结果最佳，σj,i(t)也准确。

对于上式，釆用迭代方式来不断修正σj,i(t)，即先给出一组初始σj,i(t)，代入上式计算叠加和rj(t)，则剩余噪声方差为：

(8)

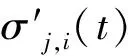
从记录道起点开始，逐点可计算出每道每点的方差。这样便完成了方差的时空变计算。将方差σj,i(t)代入(4)式即可完成随机噪声的消除。由上可见：准确求出方差σj,i(t)时，应用相邻道小波系数，但去噪仅应用σj,i(t)。这就实现了具有保真性的多道识别、单道消除思想。

将求取的σj,i(t)代入(5)式便实现了小波阈值去噪，然后向下进行下一样点的去噪处理，一直到该道最后一个样点。滑动一道进行同样处理，直到该道集内最后一道。对所有各层小波系数进行上述处理，然后小波重建便完成了横向滑动的时空变小波阈值保真去噪。

2 模型试算及实际资料处理

2.1 理论模型数据试算

图1为应用本文提出的叠前反演数据优化处理技术对理论模型数据试算的结果。图1a是信噪比为1.8的叠前道集，其中第8道和第9道下移了10ms，且信号能量为相邻道的0.6倍，以模拟具有时延、能量变化的含噪道集。图1b为应用本文基于常规多项式拟合的剩余时差校正技术消除剩余时差后的结果，可见处理后时差得以消除。图1c 是对图1b进行F-X反褶积去噪处理结果，图1b中的随机噪声得到了有效衰减，但第8道和第9道的能量经处理后变得和相邻道相近，这是多道识别、多道消除产生的结果，这个结果是通过多道信

息拟合出各道记录的振幅，破坏了道集内各道记录的相对振幅关系，将给反演结果带来致命的错误。图1d是应用横向滑动时空变小波阈值保真去噪技术处理后的结果，可见去噪结果较图1c更为彻底，图中几乎没有噪声存在，更为可喜的是第8道和第9道保持着原来的能量，与相邻道能量关系与去噪前保持一致。

2.2 实际地震资料处理

图2给出了实际地震道集分时窗和分波形时差校正处理的效果对比。图2a为未进行时差校正的实际地震资料CMP道集，图2b为分时窗校正处理结果，而图2c为分波形校正处理结果。对比可见，分波形校正较分时窗校正的时差校正效果明显更好。

图1 理论模型数据应用本文提出技术优化处理的结果a 具有时延和能量变化的含噪叠前道集; b 应用本文提出的优化处理技术消除剩余时差后的结果; c 对图1b进行F-X反褶积去噪处理结果; d 对图1b应用本文提出的优化处理技术去噪结果

图2 实际地震资料CMP道集(a)的分时窗(b)和分波形(c)时差校正处理效果对比

图3为对实际地震资料含噪道集进行不同方法去噪处理的效果对比。图3a为含噪道集;图3b为F-X反褶积去噪结果;图3c为文献[15]的时空变小波阈值去噪结果;图3d为本文横向滑动时空变小波阈值去噪结果。F-X反褶积是基于多道预测、多道消除思路的去噪技术，处理时用相邻道的信息拟合处理道信息，严重地损害了相邻道之间的相对振幅关系及波形特征(见图3b)。而应用文献[15]提出的时空变小波阈值去噪后(见图3c)，各道记录在同一时间上的相似性增强，破坏了各道记录的相对能量关系及波形特征。由图3d可见，应用本文提出的横向滑动时空变小波阈值去噪结果背景干净，随机噪声得到了有效消除，且很好地保持了有效信息的波形形态和相对能量关系。

图4为应用本文提出的技术优化处理前、后近道叠加剖面(图中黑色)和远道叠加剖面(图中红色)叠合的效果对比。图4a为优化处理前的道集叠加剖面;图4b为优化处理后的道集叠加剖面;图4c 和图4d分别为对应图4a和图4b中椭圆框的局部放大显示。由图4可见，经叠前优化处理后，近、远道叠加结果更趋重合，这是由于优化处理消除了剩余时差和噪声，使近道和远道记录的波形趋于一致，进而使用于叠前反演分析的反射波振幅来自于同一时间。

图3 实际地震资料含噪道集的不同方法去噪处理效果对比a 含噪道集; b F-X反褶积去噪结果; c 时空变小波阈值去噪结果; d 横向滑动时空变小波阈值去噪结果

图4 优化处理前(a)、后(b)近道叠加剖面(黑色)和远道叠加剖面(红色)叠合及其对应的局部放大显示(c和d)

图5为应用本文技术优化处理前、后道集的AVO响应效果对比。图5a至图5d分别为优化处理前的CRP道集、正演道集、3°～30°入射角的叠加剖面(图中插入了测井曲线)及AVO响应;图5e 至图5h则分别为对应以上各图的优化处理后结果。对比优化处理前(图5a)、后(图5e)的CRP道集，可见图5e中有效信号的同相轴校平，层间噪声得以消除。结合地层解释横线对比优化处理前(图5b)、后(图5f)的正演道集，图5f中的每一解释层位均与叠加剖面中插入的测井曲线一致，而图5b则层位对比困难。图5d和图5h中粉红线是优化前、后正演道集反射振幅随角度变化趋势；而红线是优化前后实际道集的反射振幅随角度变化趋势。从优化处理前(图5d)、后(图5h)AVO响应的对比可以看出，经优化处理后，两种趋势曲线在纵向上更靠近，且没有改变二者的变化趋势。显然，图5h的AVO现象更为明显。

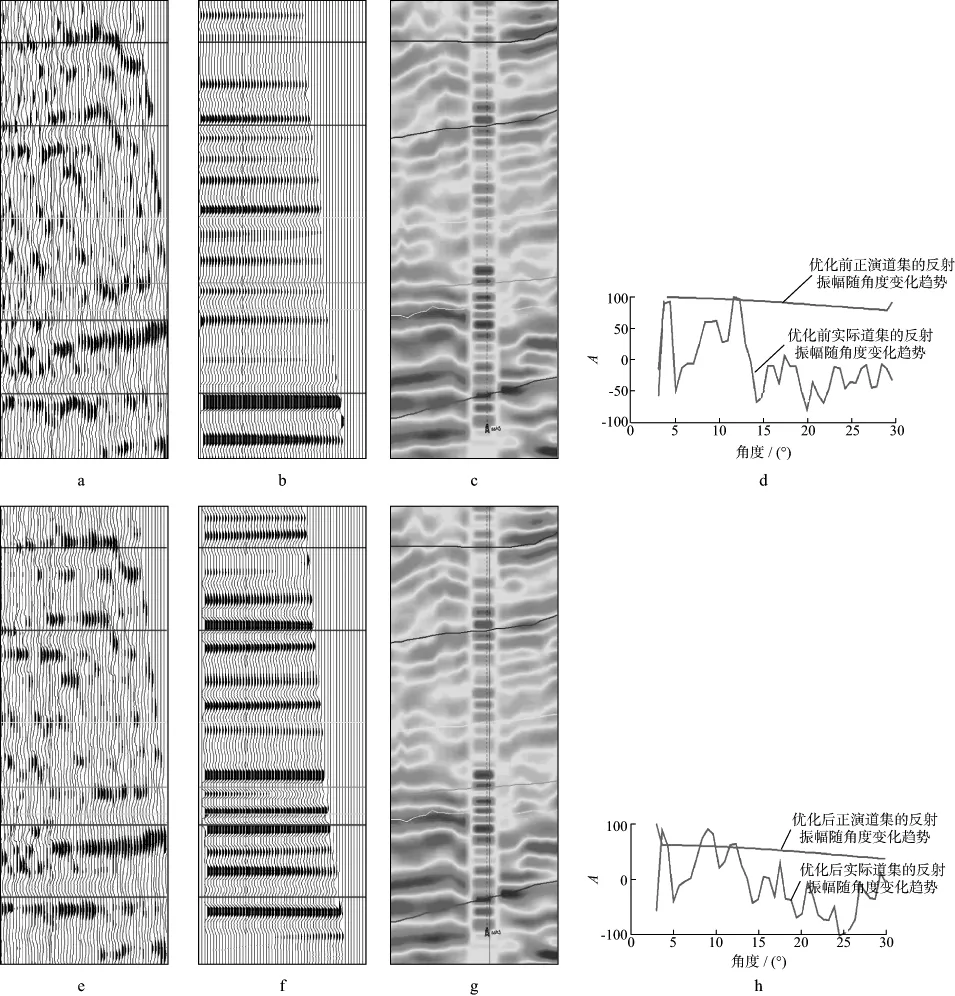
图5 应用本文技术优化处理前、后道集的AVO响应效果对比a 优化处理前的CRP道集; b 优化处理前的正演道集; c 优化处理前的3°～30°入射角叠加剖面; d 优化处理前的AVO振幅曲线; e 优化处理后的CRP道集; f 优化处理后的正演道集; g 优化处理后的3°～30°入射角叠加剖面; h 优化处理后的AVO振幅曲线

3 结束语

通过上述理论论述和模型数据测试及实际地震资料处理验证，可以得出以下结论。

1) 常规地震资料处理流程及部分处理技术已不能满足叠前反演的需要，叠前反演前必须进行数据优化处理。

2) 有效信息排齐及尽可能地保真去噪是叠前反演数据的最基本需求。

3) 利用常规多项式拟合技术校正叠加结果，保证了叠加结果位置的准确性;由分波形时差校正取代分时窗时差校正，提高了剩余时差校正的精度。

4) 多道识别、单道消除的横向滑动时空变小波阈值去噪技术能够保证去噪过程中的保真性。

5) 利用本文提出的时差校正及保真去噪技术实现了叠前反演数据优化，在理论模型数据及实际地震资料处理中的成功应用证明了这两项技术的正确性及适应性。

参 考 文 献

[1] Veeken P C H,Silva M D.Seismic inversion methods and some of their constrains[J].First Break,2004,22(1):47-70

[2] Whitcombe D N.Elastic impedance normalization[J].Geophysics,2002,58(1):60-62

[3] Connolly P.Elastic impedance[J].The Leading Edge,1999,18(4):438-452

[4] 张永刚.地震波阻抗反演技术的现状和发展[J].石油物探,2002,41(4):385-390

Zhang Y G.The present and future of wave impedance inversion technique[J].Geophysical Prospecting for Petroleum,2002,41(4):385-390

[5] 管路平.地震叠前反演与直接烃类指示的探讨[J].石油物探,2008,47(3):228-234

Guan L P.Pre-stack inversion and direct hydrocarbon indicator[J].Geophysical Prospecting for Petroleum,2008,47(3):228-234

[6] 仝兆岐.储层地震技术新进展[M].东营:石油大学出版社,2004:98-135

Tong Z Q.The New Progress of The reservoir Seismic Technique[M].DongYing:Petroleum university Press,2004:98-135

[7] 苑书金.叠前地震反演技术的进展及其在岩性油气藏勘探中的应用[J].地球物理学进展,2007,22(3):879-886

Yuan S J.Progress of pre-stack inversion and application in exploration of the lithological reservoir[J].Process in Geophysics,2007,22(3):879-886

[8] 杨迪琨,胡祥云.含噪声数据反演的概率描述[J].地球物理学报,2008,51(3):901-907

Yang D K,Hu X Y.Inversion of noisy data by probabilistic methodology[J].Chinese Journal of Geophysics(in Chinese),2008,51(3):901-907

[9] 熊定钰,赵海珍,陈海云，等.保持地震记录叠前AVO属性的噪声衰减方法[J].石油地球物理勘探，2010,45(6):856-860

Xiong D Y，Zhao H Z，Chen H Y,et al.Noise attention method based on the preserved preserved prestack AVO attribute[J].Oil Geophysical Prospecting,2010,45(6):856-860

[10] 鲍熙杰,赵海波.CRP道集优化处理对叠前反演的影响[J].石油地质与工程，2013,27(1):39-41

Bao X J,Zhao H B.effects analysis of CRP gather optimal processing on prectack inversion[J].Exploration and Development Institute，2013,27(1):39-41

[11] Singleton S．The effects of seismic data conditioning on prestack simultaneous impedance inversion[J].The Leading Edge,2009,28(1):772-781

[12] 刘力辉,杨晓,丁燕，等.基于岩性预测的CRP道集优化处理[J].石油物探，2013,52(5):482-488

Liu L H,Yang X,Ding Y,et al.CRP gather optimization processing based on lithological prediction[J].Geophysical Prospecting for Petroleum,2013,52(5):482-488

[13] 夏洪瑞,陈德刚，周开明.剩余动校正量的拾取与消除[J].石油地球物理勘探,1997,32(6):872-877

Xia H R,Chen D G,Zhou K M.Pickup and removal of residual normal moveout[J].Oil Geophysical Prospecting,1997,32(6):872-877

[14] 夏洪瑞,董江伟,邹少峰,等.常规二次多项式拟合地震数据[J].石油物探，2006,45(5):492-496

Xia H R,Dong J W,Zou S F,et al.Normal quadratic polynomial fitting seismic data[J].Geophysical Prospecting for Petroleum,2006,45(5):492-496

[15] 夏洪瑞,葛川庆,彭涛.小波时空变阈值去噪方法在可控震源资料处理中的应用[J].石油地球物理勘探，2010,45(01):23-27

Xia H R,Ge C Q,Peng T.Application of wavelet time-space-varying threshold denoising method in vibroseis seismic data processing[J].Oil Geophysical Prospecting,2010,45(1):23-27