基于MCMC的分位回归AR-ARCH模型的贝叶斯分析

曾惠芳， 熊培银

( 1.湖南科技大学 商学院； 2.湖南科技大学 信息与电气工程学院: 湖南 湘潭 411201 )

金融市场波动性是近年来金融理论研究中较为活跃的一个课题，其中波动率是衡量金融资产风险的重要指标.传统的金融时间序列模型假设收益率序列服从正态分布，但是，近年来的大量实证研究表明，金融市场上绝大多数资产收益率序列的特征往往无法用一些标准的金融时间序列模型来刻画，比如尖峰厚尾性、非对称性等，尤其是当条件方差不存在时，传统的GARCH模型很难实现对金融市场波动特征的刻画.为了更全面和准确地描述金融时间序列的波动特征，研究者们提出了一些更加灵活和稳健的分位回归方法.如：Koenker等讨论了异方差模型的分位估计[1]，且提出了分位自回归条件异方差模型[2]，并推导了其估计量的渐近分布；Xiao等[3]提出了分位数GARCH模型，并给出了该模型的两步估计方法以及估计量的渐近性质；Chen等[4]提出了ARCH模型的一步估计，并提出了分位回归模型的格兰杰因果检验；王新宇等[5]利用MCMC方法对间接TARCH-CAViaR模型进行了贝叶斯分析，并分析了中国股市的风险价值.虽然对ARCH模型的分位回归分析取得了一些成果，但它仍处于起步阶段，有待于进一步研究.本文讨论了分位回归ARCH模型的结构特征及其相应的估计方法，提出了AR-ARCH模型的两步估计方法，并对其进行了仿真验证分析.

1 模型结构分析

假设随机变量{yt}服从如下的AR-ARCH过程：

(1)

yt=σtet=(α0+α1|yt-1|+…+αq|yt-q|)et，

(2)

因此，分位回归ARCH模型可用如下的随机系数分位回归AR来表示：

yt=σtet=(α0+α1|yt-1|+…+αq|yt-q|)et=α0(et)+α1(et)|yt-1|+…+αq(et)|yt-q|，

(3)

因为|yt-j|以及系数都大于0， 所以它是关于et的单调递增函数.相应地，yt的条件分位数函数为

(4)

在经济系统中，经济变量是互相联系的，因此，在对资产收益率时间序列建模时，需要在分位回归ARCH模型中引入其他经济解释变量,即

yt=a0+a1yt-1+…+apyt-p+ap+1x1t+…+ap+vxv t+εt,

(5)

并假设残差项为

εt=(α0+α1|εt-1|+…+αq|εt-q|+αq+1|x1t|+…+αq+v|xv t|)et，

(6)

(7)

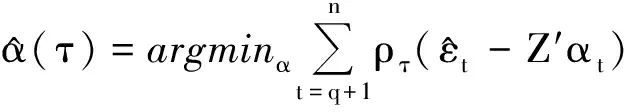
2 模型的贝叶斯估计

为了实现分位回归ARCH模型的贝叶斯推断，可以假设模型为

(8)

(9)

其中W=(wp+1,…，wn)′.假设参数α的先验分布为扩散先验分布，即π(α)∝1， 根据贝叶斯公式，可以实现对参数α的贝叶斯分位回归估计.

3 仿真试验和分析

图1分别给出了残差项服从标准正态分布、自由度为3的t分布和标准柯西分布的时间序列样本轨迹图.从图1可以看出：扰动项服从柯西分布的时间序列，其异常点最多；其次是扰动项服从t分布的时间序列;正态分布的异常点相对较少.

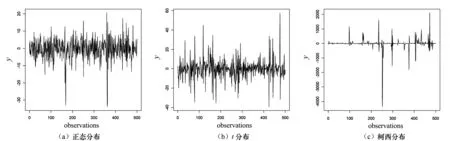
图1 时间序列样本轨迹图

选择先验分布为均匀分布，可以由M-H算法模拟得到各个参数的边缘后验分布.在模型运行的过程中，一共迭代了11 000次.为确保参数估计的一致性，丢弃开始时的1 000次迭代，用1 001次到11 000次迭代得到的样本来估计参数.图2给出了残差项服从标准正态分布时，模型参数在不同概率水平(τ=0.05,0.25,0.5,0.75,0.95)下的后验密度直方图.由于篇幅所限，本文略去残差项服从自由度为3的t分布和标准柯西分布情况下的模型参数估计的后验密度直方图.从图2可以看出，不同情况下参数的后验估计直方图都呈倒钟型，说明MCMC模拟过程是平稳的，即该MCMC抽样算法能有效地模拟分位回归ARCH过程中各参数的边缘后验分布.

表1给出了当分位数τ=0.05,0.25,0.5,0.75,0.95时参数的后验估计.从表1可知，扰动项服从正态分布或t分布时，因为其本身是对称分布，所以参数的估计也是对称的.当扰动项服从正态分布时，α0(0.05)=-9.415 0,α0(0.95)=9.896 0; 当扰动项服从t分布时，α0(0.05)=-14.881 0,α0(0.95)=14.020 2.由于t分布具有厚尾性，当分位数相等时，t分布的尾部概率比正态分布更大.因为柯西分布比t分布具有更厚的尾部特征，所以其分位数在尾部的绝对值更大.模型参数的估计结果与真实值比较接近，这进一步说明了该方法的有效性.

图2 不同概率水平下参数的后验密度(残差项服从标准正态分布)

表1 参数的贝叶斯分位回归估计

参考文献：

[1] Koenker R, Zhao Q. L-estimation for linear heteroscedastic models[J]. Journal of Nonparametric Statistics, 1994,3:223-235.

[2] Koenker R, Zhao Q. Conditional quantile estimation and inference for ARCH models[J]. Econometric Theory, 1996,12:793-813.

[3] Xiao Z, Koenker R. Conditional quantile estimation for generalized autoregressive conditional heteroscedasticity models[J]. Journal of the American Statistical Association, 2009,104(488):1696-1712.

[4] Chen C W S, Gerlach R, Wei D C M. Bayesian causal effects in quantiles: accounting for heteroscedasticity[J]. Computational Statistics & Data Analysis, 2009,53:1993-2007.

[5] 王新宇,宋学锋.间接TARCH-CAViaR模型及其MCMC参数估计与应用[J].系统工程理论与实践,2008(9):46-51.

[6] 曾惠芳,朱慧明,李素芳.基于MH算法的贝叶斯分位自回归模型[J].湖南大学学报：自然科学版,2010,37(2):88-92.

[7] 朱慧明,王彦红,曾惠芳.基于逆跳MCMC的贝叶斯分位自回归模型研究[J].统计与信息论坛,2010,25(1):9-13.