基于Box-Jenkins方法的甘肃省GDP时间序列分析建模与预测

李生彪, 彭建奎

( 兰州文理学院， 甘肃 兰州 730000 )

在国民经济运行过程中，GDP是衡量一个国家或地区经济发展状况的重要指标，也是政府在制定经济发展战略和政策时的一个重要依据；因此，对一个国家或地区的GDP进行分析和预测具有非常重要的意义.20世纪70 年代，G.P.Box和G.M.Jenkins提出了ARIMA 模型法[1]，该模型是在建模之前先将非平稳时间序列转化为平稳的时间序列，然后再运用 ACF图和PACF图对得到的平稳时间序列选择最佳的ARIMA模型.由于传统的灰色理论、生长曲线、指数平滑法等方法只适合于具有某种典型趋势特征变化的现象的预测,而甘肃省在改革开放以来特别是在西部大开发以来GDP增长快速，其GDP的时间序列数据并不总是满足这种典型趋势特征，这使得这些传统模型产生的误差项不一定完全是具有随机性质的,从而会影响对它的预测效果.本文利用SPSS软件，对甘肃省GDP的年度数据进行了时间序列分析，并基于Box-Jenkins方法建立了甘肃省GDP的时间序列ARMA模型，最后运用该模型对未来4年甘肃省的GDP进行了预测.

1 Box-Jenkins方法简介

Box-Jenkins方法是关于时间序列分析、预测及控制的一整套方法，也称作传统的时间序列建模方法.该方法把时间序列建模分为3个阶段，即模型类型识别阶段、模型的参数估计阶段以及基于模型的预测阶段[2].在实际应用中，Box-Jenkins方法的常见模型形式为：若时间序列值xt是现在干扰值εt和过去干扰值εt-i以及过去的序列值xt-i的线性组合，则称此模型为自回归移动平均模型;相应地，序列xt称为自回归移动平均序列，称

xt=φ1xt-1+φ2xt-2+…+φpxt-p+θ1εt-1+θ2εt-2+…+θqεt-q

(1)

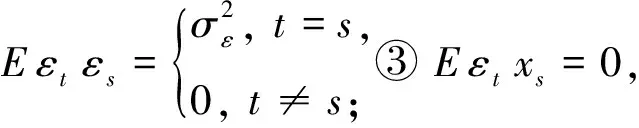
2 甘肃省GDP时间序列分析建模

2.1 甘肃省GDP数据的分析

甘肃省1978—2012年的GDP数据[5]如表1所示，图1是其时间序列的折线图.

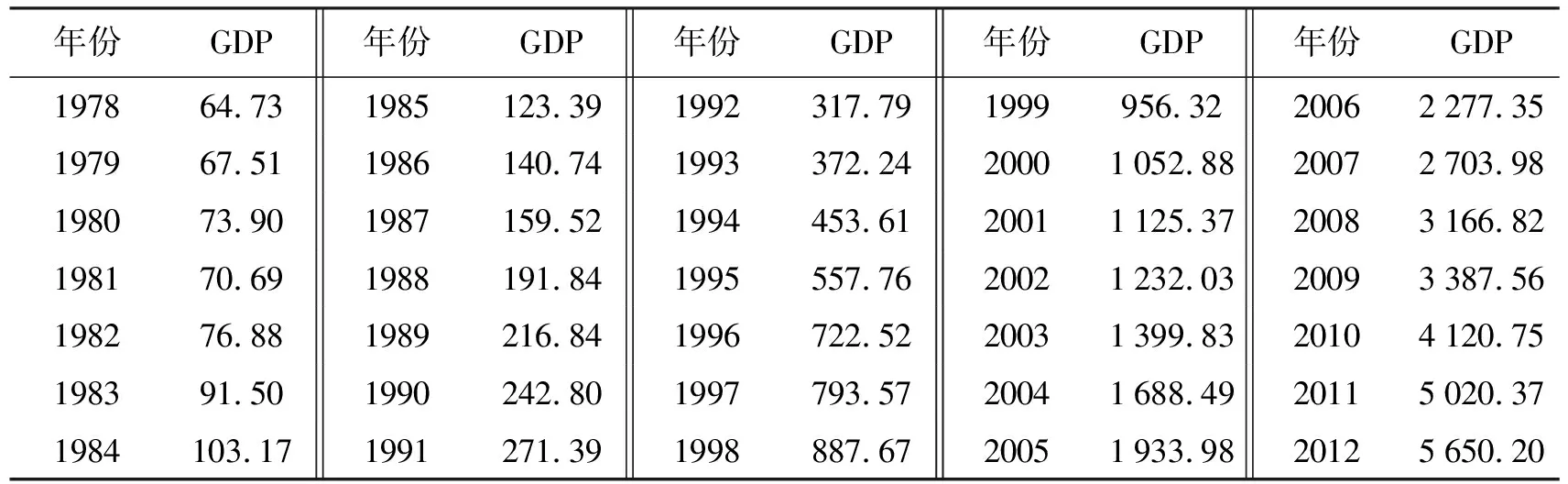
表1 1978—2012年甘肃省GDP 亿元

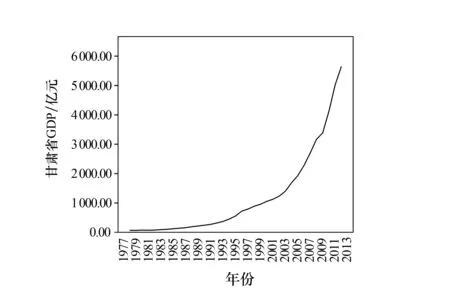
图1 1978—2012年甘肃省GDP数据时间序列的折线图

从图1可以看出，甘肃省的GDP在1978—1994年增长缓慢，但从1995年开始呈现出一种指数增长的趋势.由此可知该时间序列是一个非平稳的时间序列.我们首先通过对甘肃省的GDP数据取对数并做一阶差分，将其转化为线性趋势，使该时间序列达到平稳.取对数并做一阶差分后得到的甘肃省GDP数据时间序列图如图2所示.由图2可以看出，取对数并做一阶差分后的甘肃省GDP数据时间序列基本达到平稳.下面对该数据进行ACF图和PACF图分析，进行模型的识别和定阶，以最终找到最佳的时间序列模型.

2.2 模型的识别与定阶

首先根据甘肃省GDP时间序列模型的ACF图和PACF图(见图3)建立相应的ARMA模型.从图3可看出，PAC截尾,而AC拖尾,因此可判定对GDP数据差分后的序列适合AR模型,即原GDP数据序列适合模型ARIMA(p,1,0)，也就是说，对于原GDP数据序列而言,其可供选择的模型有ARIMA(1,1,0)和ARIMA(2,1,0).

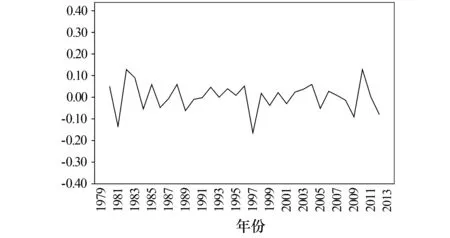
图2 对数变换和一阶差分后的甘肃省GDP数据时间序列图

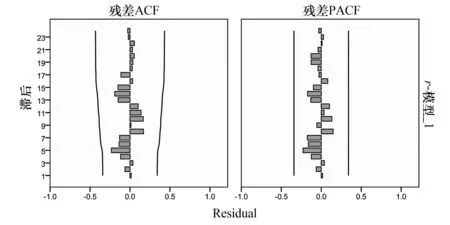
图3 1978—2012年甘肃省GDP差分序列的ACF和PACF图

下面进行参数估计.文献[6-7]表明，当最小信息准则AIC和Schwarz-Bayes准则SIC的值最小时，所对应的模型为预测的最佳模型.在参数估计的过程中,同时进行模型的残差白噪声检验.计算后的主要效果指标值如表2所示.从表2容易看出,ARIMA(2,1,0)是甘肃省GDP序列的最佳拟合预测模型,模型中具体的系数及显著性检验的计算结果如表3所示.由表3数据可以得到如下的甘肃省GDP预测公式：

Δyt=0.357 695Δyt-1+0.357 896Δyt-2,

(2)

yt=1.357 695yt-1+0.000 202yt-2-0.357 896yt-3.

(3)

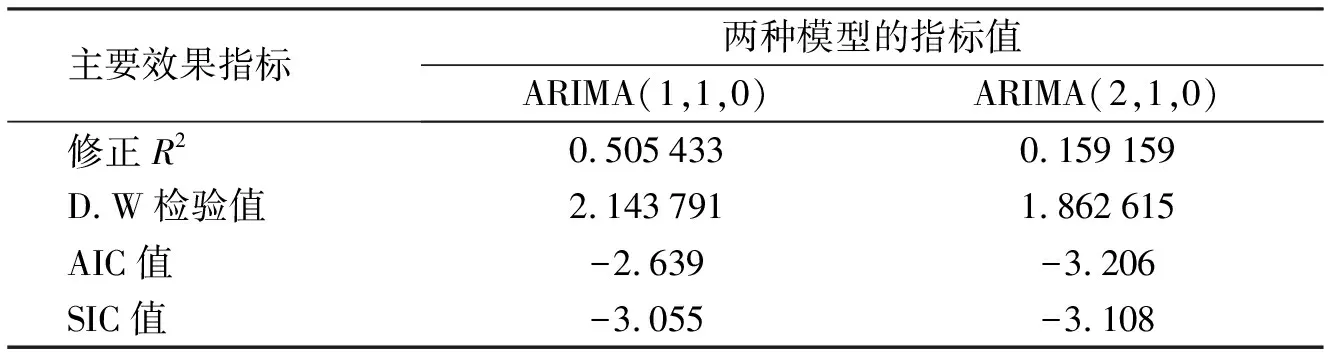
表2 GDP序列的两种ARIMA模型的效果指标比较表

表3 ARIMA(2,1,0)模型的系数及显著性检验表

2.3 模型的显著性检验

显著性检验就是看模型的残差序列是否为白噪声序列.如果是，说明模型可用来预测；否则，模型不合适于用来预测.本文利用残差序列的ACF图和PACF图来检验残差序列是否为白噪声序列，检验结果如图4所示.从图4可以看出，残差序列近似为白噪声序列，这说明模型(3)可以用来拟合甘肃省GDP的时间序列.

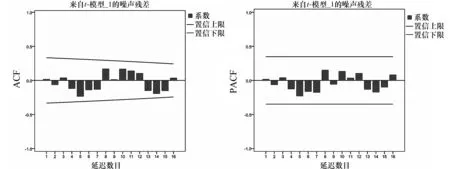
图4 残差序列的ACF图和PACF图

3 甘肃省GDP数据的预测和分析

利用模型(3)对甘肃省2009—2012年的GDP数值进行计算并与实际值进行对照,检验模型的精确度，结果见表4.从表4可知，2009—2012年的实际GDP值与计算得到的GDP值之间的相对误差均在5%以内，预测结果比较准确，由此说明模型(3)的拟合效果较好.为进一步说明拟合的效果，利用实际值和拟合值计算出模型(3)的相关系数R2=0.992 7,由此进一步验证了该模型能很好地反映出实际状况.基于此判断，利用该模型对甘肃省2013—2016年的GDP做了预测，并得到了相应的预测值(见表4)，其结果的精确度有待于今后与实际GDP指标值比较后进一步确认.

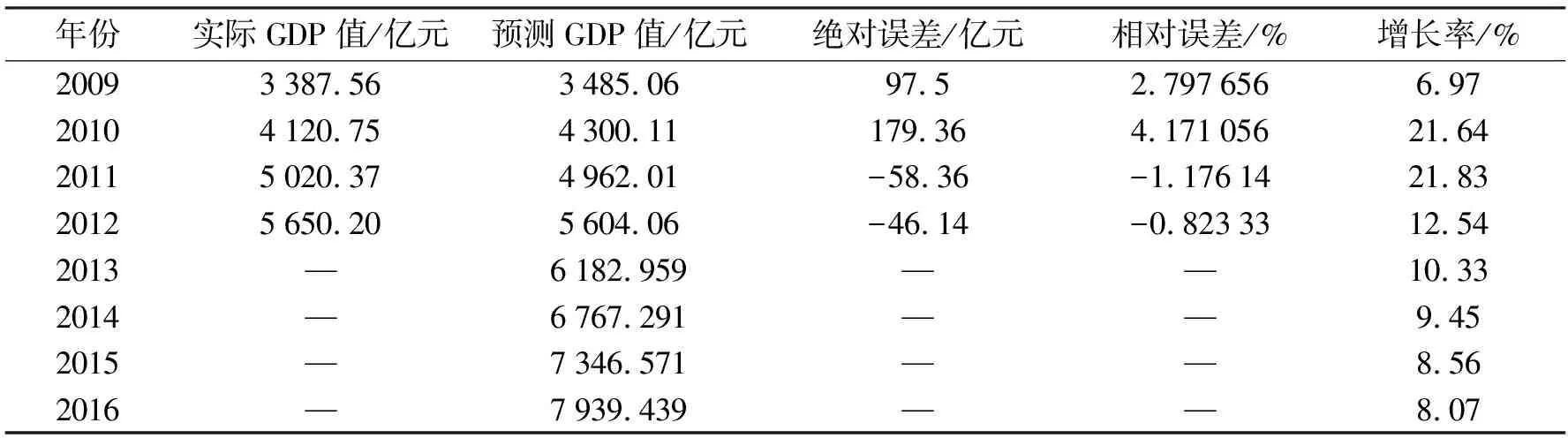
表4 预测值及与实际值的对照

4 结论与建议

本文利用SPSS软件并选取ARIMA(2,1,0)为拟合预测模型对甘肃省GDP进行了时间序列分析.实证分析表明，采用模型(3)预测甘肃省GDP取得了良好效果，而且比传统模型更为简便.另外，本文收集的时间序列分析的数据相对较多，并且由于Box-Jenkins方法不需要对发展模式做先验的假设,而且方法本身又可反复进行识别和修改,因此Box-Jenkins方法非常适合各种经济时间序列分析，尤其是短期预测.如果预测时间延长,本方法的预测误差会相对增大,因此本文中的模型(3)还有待进一步改进.

参考文献：

[1] 何书元.应用时间序列分析[M].北京：北京大学出版社，2004:5-7.

[2] 张树京.时间序列分析简明教程[M].北京:清华大学出版社，2003:27-29.

[3] 王莎莎,陈安,苏静,等.组合预测模型在中国GDP预测中的应用[J].山东大学学报:理学版，2009,44(2):56-59.

[4] 王晓鹏,曹广超,丁生喜,等.基于Box-Jenkins方法的青南高原降水量时间序列建模与预测[J].数理统计与管理，2008，27(4):1-7.

[5] 国家统计局.中国统计年鉴(1991—2011)[M].北京:中国统计出版社,2012:346-368.

[6] 汤岩.时间序列分析的研究与应用[D].哈尔滨:东北农业大学，2007.

[7] 刘宏杰.基于时间序列分析预算支出与经济增长的关系[J].商业时代，2008,32:6-7.