如何在数理方法教学中培养学生综合运用知识的能力——以留数定理在傅里叶级数展开问题中的应用为例

朱爱东， 王洪福， 田莲花， 张英俏

( 延边大学理学院 物理系， 吉林 延吉 133002 )

0 引言

数学物理方法课程的内容不仅涵盖数学的理论和计算方法，同时也涉及物理学的相关知识，因此要教好这门课程，就要求教师要具有良好的高等数学基础和深厚的物理功底.目前的数学物理方法教材[1-3]，按照知识结构一般分为两大部分：复变函数论和数学物理方程.在复变函数论部分中，解析函数的级数展开、留数定理、傅里叶变换、以及拉普拉斯变换等内容各成一章，关联性不强，因此初学这门课程的本科生在学习过程中往往局限于当前的学习内容，缺少对这门课程的系统性和应用性的深刻理解，难以将所学的各种方法和理论知识融合贯穿、活学活用.实际上，针对一个物理问题，建立数学模型之后，其解决的方法往往不只一种，并且在解题的过程中，可以将各种方法灵活地结合运用，使问题得以简化.因此，教师在教学过程中如何启发和开阔学生思路，提高学生对知识融会贯通的能力，加深学生对这门课程系统性和应用性的深刻认识，是教学中面临的重要课题.针对上述问题，本文就R(cosx,sinx)三角函数有理式的傅里叶级数展开这一问题，分别给出教师通常使用的洛朗级数[4-5]和文献中尚未报道过的留数定理两种解法，以此拓宽学生的解题思路，提高学生对知识融会贯通、综合运用的能力.

1 三角函数有理式R(cos x,sin x)的傅里叶级数展开

三角函数的特点是可以将x作为复数z的幅角，通过自变数代换z=ei x，当实变数x从0变到2π时，复变数z=ei x从z=1出发沿着单位圆|z|=1逆时针走一圈又回到z=1.这个特点使得在求傅里叶级数展开系数时，可将实函数的积分转化为复变函数的回路积分，即可以利用留数定理求傅里叶级数的展开系数.下面给出这种方法的详细过程.

首先确定这类函数的周期是2π.根据傅里叶级数展开系数的公式，半周期l=π.傅里叶级数展开公式如下：

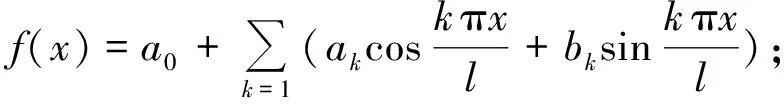
对于函数R(cosx,sinx)，可做如下处理：

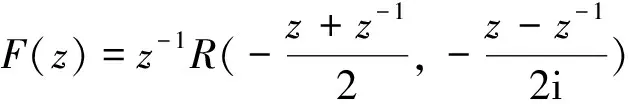
(1)

同理，可以得出

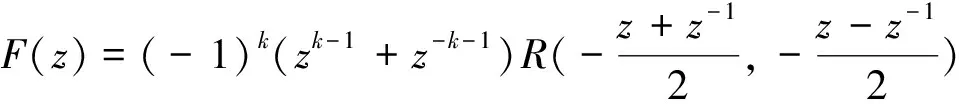
(2)

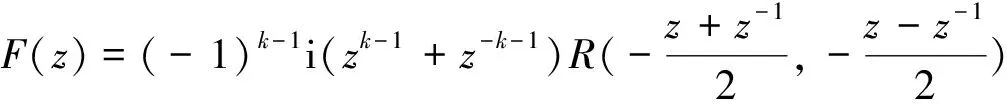
(3)

经过以上过程，即可将傅里叶级数展开问题转化为求解析函数在单位圆内的留数问题.

除了以上方法，某些特殊情况，还可以采用级数方法.当原函数转化为复变函数后，利用洛朗级数展开方法直接将其写成级数形式，再利用欧拉公式就可以得到傅里叶级数的三角函数展开形式，而不必代入傅里叶级数的系数公式，避免了积分运算.这种方法也是大多数参考书上给出的方法，但其前提条件是写成复数的洛朗级数后，必须能够利用欧拉公式重新回到三角函数形式的傅里叶级数，所以这种方法只适用于某些特殊情况.

2 解题实例

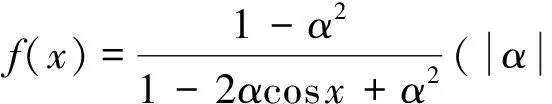
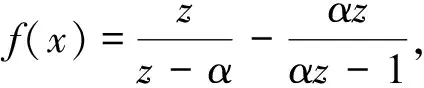
(4)

(5)

所以

(6)

这种方法需要学生对复变函数在环域上解析以及单位圆内孤立奇点的定义有深刻的理解，解题关键在于将拆分出的两个分式在单位圆内挖去奇点形成的环域上展开为幂级数，即(1)、(2)两式,其优点在于不用进行积分运算.

解法2留数定理法.该函数是以2π为周期的偶函数，因此可以将其展开为傅里叶余弦级数，且l=π，即

(7)

根据(1)和(2)式有

(8)

其中Res[f(z),zk]表示函数f(z)在第k个孤立奇点处的留数,

(9)

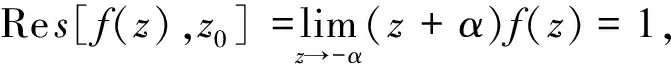
(10)

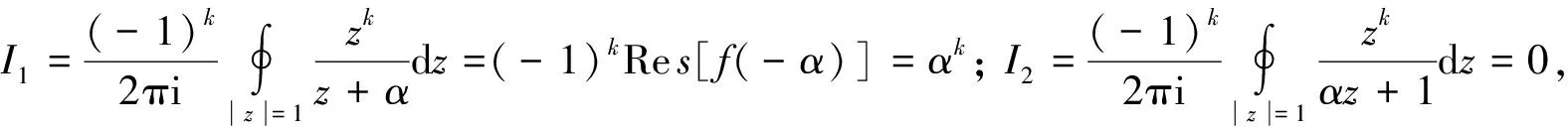
这种方法的优点是利用了傅里叶级数展开的系数公式，方法较为直接，只是计算稍显繁琐.该方法的解题关键在于能够将实变函数的定积分转换为复变函数的回路积分，并利用留数定理计算出积分，从而得到傅里叶展开系数.

3 结束语

培养学生综合运用知识的能力是数学物理教学的重要内容，因此，教师在讲解实际问题时，要引导学生拓宽思路，不拘泥于参考书已有的方法，启发学生尝试新的不同的解题方法，使学生达到对知识融会贯通、灵活运用的目的.

参考文献：

[1] 梁昆淼,刘法,廖国庆.数学物理方法[M].4版.北京:高等教育出版社,2010:1-375.

[2] 姚端正,梁家宝.数学物理方法[M].3版.北京：科学出版社,2010：1-340.

[3] 胡嗣柱,倪光炯.数学物理方法[M].2版.北京：高等教育出版社,2002：1-359.

[4] 斯颂乐,徐世良,高永椿,等.数学物理方法习题解答[M].天津：天津科学技术出版社,1982：145-146.

[5] 苗明川,龚云,任正.数学物理方法全程导学及习题全解[M].北京：中国时代经济出版社,2011：75-76.