非简并光学参量振荡器中量子态频率上转换

明 莹

( 延边大学理学院 物理系, 吉林 延吉 133002 )

参量频率转换能够产生可调谐的相干辐射和压缩光[1]，因此被广泛应用于干涉测量、精确测量和光谱学等方面，并成为量子网络的重要组成部分[2].在量子网络中， 实现量子态的单位转换的方法有很多，例如可以通过粒子湮灭或产生来实现，也可以通过参量频率上转换来实现，等等.由于参量频率上转换能够显著提高转换效率[3]，因此被认为是目前解决量子态转换的最佳方法，但在所知文献中其转换效率均低于50%.研究[4-5]表明，在共振腔内进行频率转换可以有效增强转换效率.基于文献[5]，本文提出了在光学参量振荡腔中的量子态频率上转换的方案.

1 理论模型

(1)

(2)

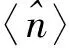
(3)

(4)

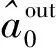
图1 实验装置图

(5)

(6)

(7)

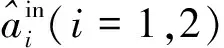
(8)

(9)

(10)

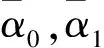
(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

用振幅和位相正交量定义X=a+a+和Y=-i(a-a+), 获得输出场谐波模的起伏为:

经过傅里叶变换后可得到：

δX0(Ω)=-1/{Ω2(iΩ+γ0+μ0)(γ+μ)+2Ω(Ω-iμ0-2iγ0σ2)(γ+μ)2+

(23)

δY0(Ω)=1/{-Ω2(iΩ+γ0+μ0)(γ+μ)+2Ω(-Ω+iμ0+2iγ0σ2)(γ+μ)2+

(24)

(25)

(26)

其中：

R1=Ω2(iΩ+γ0+μ0)(γ+μ)+2Ω(Ω-iμ0-2iγ0σ2)(γ+μ)2+4γ0(1-σ2)(γ+μ)3,

2Ω(Ω-iμ0-2iγ0σ2)(γ+μ)2-4γ0(1-σ2)(γ+μ)3,

R2=-Ω2(iΩ+γ0+μ0)(γ+μ)+2Ω(-Ω+iμ0+2iγ0σ2)(γ+μ)2+4γ0σ2(γ+μ)3,

2Ω(-Ω+iμ0+2iγ0σ2)(γ+μ)2-4γ0σ2(γ+μ)3,

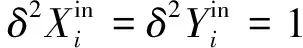
(27)

(28)

2 结果与讨论

图2 信号传递效率TX、TY和转换效率η随泵浦参数σ的变化曲线

参考文献：

[1] Burnham D C, Weinberg D L. Observation of simultaneity in parametric production of optical photon pairs[J]. Phys Rev Lett, 1970,25(2):84-87.

[2] Cirac J I, Zoller P, Kimble H J, et al. Quantum state transfer and entanglement distribution among distant nodes in a quantum network[J]. Phys Rev Lett, 1997,78(16):3221-3224.

[3] Giorgi G, Mataloni P, Marini F D. Frequency hoppping in quantum interferometry: efficient up-down conversion for qubits and ebits[J]. Phys Rev Lett, 2003,90(2):027902.

[4] Bosenberg W R, Guyer D R. Broadly tunable, single-frequency optical parametric frequency-conversion system[J]. J Opt Soc Am B, 1993,10(9):1716-1722.

[5] Bai Y F, Zhai S Q, Gao J R, et al. Noise-free frequency conversion of quantum states[J]. Chin Phys B, 2011,20(3):034207.

[6] Jen H H, Kennedy T A B. Efficiency of light-frequency conversion in an atomic ensemble[J]. Phys Rev A, 2010,82(2):023815.

[7] Pooser R C, Marino A M, Boyer V, et al. Low-noise amplification of a continuous-variable quantum state[J]. Phys Rev Lett, 2009,103(1):010501.

[8] Gardiner C W, Collett M J. Input and output in damped quantum systems: quantum stochastic differential equations and the master equation[J]. Phys Rev A, 1985,31(6):3761-3774.

[9] Reynaud S, Fabre C, Giaocobino E. Quantum fluctuations in a two-mode parametric oscillator[J]. J Opt Soc Am B, 1987,4(10):1520-1524.

[10] Collett M J, Gardiner C W. Squeezing of intracavity and traveling-wave light fields produced in parametric amplification[J]. Phys Rev A, 1984,30(3):1386-1391.