地铁车站换乘通道合理长度评估方法*

李得伟 尹浩东

（北京交通大学交通运输学院，100044，北京∥第一作者，副教授）

地铁车站换乘通道合理长度评估方法*

李得伟 尹浩东

（北京交通大学交通运输学院，100044，北京∥第一作者，副教授）

地铁车站换乘通道的长度对地铁客流组织、乘客出行具有重要的作用。针对地铁换乘站换乘通道长度合理性的问题，考虑乘客的差异性，研究了换乘通道长度对客流的影响机理；提出了地铁车站合理换乘通道长度的理论计算方法，并进行了仿真分析。通过对北京地铁崇文门和复兴门换乘站进行的实例研究，提出了换乘通道合理长度的优化建议。研究发现，地铁换乘通道长度与宽度共同决定了通道的客流集散效果，适当增加通道长度能有效缓解客流冲击；但随着地铁换乘通道长度的增加，长通道缓解客流对站台冲击的效果会减弱。所提出的建议可供地铁换乘车站设计作参考。

地铁；换乘通道；合理长度；评估

First-author'saddressSchool of Traffic and Transportation，Beijing Jiaotong University，100044，Beijing，China

我国城市轨道交通发展已进入高峰期，在多条线路条件下，换乘站是全网运营的关键。通道换乘在各大换乘车站被广泛采用。然而，有关换乘通道的长度问题在设计时没有具体规定，仍无法量化评定和计算。北京地铁从服务人性化的角度认为，新建线路间的换乘通道距离应控制在100 m。实际上，换乘通道的长度需要有一个合理取值。换乘通道过短，就达不到客流缓冲的目的，为客流集散安全埋下隐患；换乘通道过长，则会带来乘客出行时间增加、舒适度下降、能耗增加等问题。

目前，国内外既有研究多集中于换乘通道宽度的合理确定和通过能力的计算方法，我国的《地铁设计规范》中规定了通道的宽度和最大通过能力［1］。文献［2］探讨了地铁车站客流服务水平与通道宽度的关系，给出了通道各等级服务水平下的乘客速度、密度等。文献［3］提出了基于排队论的地铁人行通道宽度的合理取值方法。文献［4］用统计的方法对地铁换乘通道乘客走行时间规律进行了研究。文献［5］基于高峰时段客流量分别给出了单双向通道宽度的计算方法。以上均是对通道设计中合理宽度的计算研究，对通道合理长度的研究仍是一片空白。

而实际上，地铁换乘通道长度的设计需要考虑工程可实施性、换乘安全、乘客服务人性化及换乘客流集散等多重因素。本文重点从客流的角度，以换乘通道对客流冲击的缓解作用为切入点，在深入探讨乘客群在通道内的行为特性和集散机理的基础上，研究换乘通道合理长度的量化评估与计算方法。

1 换乘通道长度对客流的影响分析

《地铁设计规范》非常重视换乘通道宽度的设计，这主要是既有理论认为影响通道通过能力的因素主要是通道宽度W。W的计算如式（1）所示。

式中：

Q——换乘通道的超高峰客流量；

θ——不均衡系数；

C通道——换乘通道断面单位宽度的最大通行能力。

由式（1）可知，只要通道宽度满足需要，无论通道长度多少，其通过能力不变。式（1）未考虑实际中存在的两个事实：①乘客具有异质性，不同乘客的步行速度存在差异；②地铁是一个联动系统，各部分的通过能力之间互相影响。本文针对这两个客观事实，对换乘通道通过能力问题进行深入探讨。

根据一项北京地铁换乘通道的乘客步速调查显示，乘客步速最大可达到1.93 m/s，而最小步速接近0.5 m/s［6］。可见，当考虑乘客速度差异时，通道内的客流情况会发生变化，不同速度的乘客会不同时到达通道末端。从而导致单位时间内通过某一断面的人数因通道长度的不同而不同。反映出的现象是通道和站台拥挤程度不同，这种长通道对客流的“稀释”作用已经广泛地被用于地铁客流组织中。

为量化研究换乘通道长度对拥挤程度的影响，对如图1所示的单向换乘通道（长L×宽W）进行研究。假定有一批换乘客流包含300名乘客，按步行速度分为3类人群，乘客构成如表1所示。

图1 单向换乘通道示意图

表1 换乘客流人员构成

考虑到不同拥挤条件下乘客的个体速度能够发挥的条件不同，因此，针对不同拥挤条件分别进行研究。

1.1 自由流条件下

当换乘通道宽度满足自由流要求时（即允许速度高的人群任意超越速度低的人群），在通道的特定位置（如出口端P1）选取客流测量点，考查不同测量点的客流量变化情况。

选取不同人群分别到达测量点的时间（t1，t2，t3）、时距（g1，g2）作为基本指标，用单位时间内离开换乘通道的人数（即测量点P1的流率qp1）作为考察通道长度对站台冲击的效果指标：

式中：

Q总——总换乘人数；

t——所有旅客从通道入口开始直到通过P1点的总时间。

由于换乘客流到达测量点P1需要一定时间，扣除这部分时间后的有效通过时间为（t3-t1），因此，实际单位时间内测量点p1的有效流率为：

当换乘通道长度从25 m起分别以25 m间隔递增到300 m时，可以分析计算出在不同的换乘通道长度下，3类人群分别到达通道出口端的时间、时距，并计算测量点（换乘通道末端）的流率和有效流率，如表2所示。从表2可以看出，由于人群的速度不同，当换乘通道长度逐渐增加时，不同人群先后到达换乘通道末端的时距逐渐增大，从而导致人群对换乘通道的占用时间不同，实际单位时间内离开换乘通道到达另一站台的人数也不同。qp1有效的值不仅反映了客流对站台的冲击程度，也间接反映了通道内的客流压力。

表2 不同换乘通道长度对客流指标的影响

以入口端为始点，一般选取换乘通道的1/4处、1/3处、1/2处（分别如图2中P2、P3、P4所示），观

察客流流率随换乘通道长度的变化情况。从图2可见，较长的换乘通道长度能够缓解客流对换入车站站台的冲击，但随着换乘通道长度的逐渐增加，这种缓解作用逐渐削弱。由此推断，换乘通道内部的拥挤程度也随着换乘通道长度的增加而减小，且随着换乘通道长度的逐渐增加，这种缓解作用逐渐削弱。长度为L的换乘通道内，假设有一测量点x，该点客流流率qx可表示为

式中：

Lx——测量点x距换乘通道入口端的长度；

v均——乘客平均速度，其取值可以根据设计服务水平的要求［3］确定。

从式（4）可以看出，客流量越大，换乘通道内任意一点流率越高；客流量相同条件下距离换乘通道入口端越远，该测量点的流率就越低。也就是说，在自由流条件，当换乘客流量不变时，换乘通道出口端的客流流率与换乘通道长度成线性反比关系，换乘通道长度越长，则流率越低，换乘客流对站台的冲击就越小。

1.2 拥挤流条件下

当换乘客流达到一定量时，换乘通道的宽度无法满足自由流行走时，产生排队现象。此时乘客之间距离较近，除了队首的少数乘客外，其他乘客均无法实现自由超越较之更慢的乘客，乘客之间的速度差异也很小。

随着换乘通道距离增加，乘客的平均步行速度也增加，乘客之间的速度差越来越大，不同速度的乘客群在换乘通道中也逐渐成形。当乘客群完全成形后，乘客之间的速度完全分化，乘客群按照速度分为多个群体，此后情况与自由流完全一致。

现仍然以3类人群为例。换乘客流中的乘客由于拥挤，初始速度都较低，但处于队首的乘客由于前方没有障碍首先开始加速和分化，致使前方乘客与后方乘客时距增加；当时距增加到一定程度时，后方的乘客也开始分化，以此类推，直到最后乘客分化完成。当换乘通道足够长时，总有一个时刻Tc，在该时刻前队伍完全分化为3个群体。

当客流量非常大时，换乘通道断面客流量接近通道最大通行能力qc（约4 500人/（h·m））时，由于前方乘客加速产生的空隙很快被后方乘客填充，队伍很难达到分化状态，乘客之间的速度差异也很小。此时，受到换乘通道宽度的影响，换乘通道内任意一点的流率等于通道最大通行能力。此时，换乘客流全部通过换乘通道花费时间可以表示为

式中：

t0——客流分化时间。

2 换乘通道合理长度的计算方法

当站台面积较小时，持续的客流冲击将导致站台上客流爆满，引发安全问题。为了便于研究客流量与换乘通道长度之间关系，定义车站的列车到站间隔时间为ΔT，岛式站台两侧列车下车人数分别为Q下1、Q下2，进站流率为q进，站台上人均占用面积为ρ，站台的容纳面积为A站台，则站台的客流安全条件为：

从式（6）可以看出，缩短列车到站间隔、限制进站流量、限制换乘流量，均可有效保证站台容纳能力满足需要。

将式（3）代入式（6），可得换乘通道的最小长度为

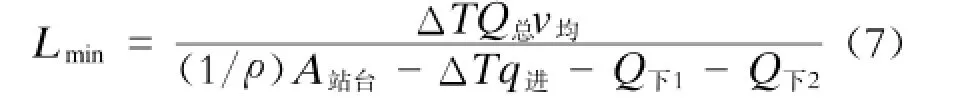
在列车间隔不变的情况下，换乘通道的最大经济长度为

式中，Qc为换乘通道最大容许通行量。

3 仿真分析

由于客流规律和乘客行为较难在理论计算中体现，采用计算机模拟法进行进一步仿真试验研究。本次采用SRail仿真软件模拟换乘乘客通过换乘通

道的行为，通过对仿真过程的观察和对仿真输出数据的处理，对换乘通道长度和换乘通道出口端流量之间的关系做定量分析。本次设计两组试验：

1）基本仿真试验——假设换乘通道长度与出口端客流量间有一定相关性，并控制仿真过程中如下条件不变：①换乘通道宽度不变，为4 m；②换乘客流量不变，为300人；③换乘客流速度不变，为高速2 m/s、中速1.5 m/s、低速1 m/s，且高、中、低速度的乘客人数比例为3∶5∶2。

2）拓展仿真试验：在基本试验的基础上，改变部分控制变量：①仅改变换乘客流量，其分别为100人、300人、500人；②仅改变换乘客流速度结构，使高、中、低速之比分别为5∶3∶2、3∶5∶2及2∶3∶5。

2次仿真试验的结果分别如图3、4、5所示。

图3 基本仿真试验换乘通道长度与出口端断面流量关系图

图4 不同换乘客流量对出口断面流量的影响（高、中、低速度的乘客人数比例为3∶5∶2时）

图5 换乘客流量为300人时不同客流速度结构对出口断面流量的影响

通过对多次仿真试验数据进行Pearson相关性检验发现，换乘通道长度与断面流量在0.01水平双侧相关性上达到了0.972。由此，可证明换乘通道长度与断面流量具有较强的相关性。

进一步对不同换乘客流量条件下的换乘通道断面流量与换乘通道长度的关系进行仿真分析，结果如图4所示。由图4可以发现，换乘客流量越大，断面流量也越大；换乘客流量大的断面流量下降趋势要快。

换乘客流量为300人时，不同客流速度结构对断面流量的影响如图5所示。由图5可以看出，高、中、低速度的乘客人数比例为5∶3∶2的客流结构由于速度快产生了较高的断面流量，而另外2种速度结构的断面流量基本一致。

4 案例分析

作者选择北京市地铁网络中客流量较大且符合换乘通道换乘的崇文门站和复兴门站作为实例分析。2012年10月21日，对车站的A站台、Q下1、Q下2、换乘量和换乘通道的L、W及分时段各断面客流量等参数进行调研，客流统计时段为20 s。

4.1 换乘通道对客流冲击的缓解效果

表3为崇文门换乘站调研的有关参数。

表3 崇文门站各换乘通道参数及测量点位置

选择换乘通道的入口处、1/4处和出口处进行流量分析（如图6及图7），发现3处断面客流总量基本一致，但波动程度却相差较大。其具体表现为：换乘通道出口处分时段客流量的波峰与波谷的差值较小，客流总体趋势较为均衡，从而减轻了换乘客流对站台的冲击程度。因此，换乘通道对缓解客流冲

击有显著的作用。

结合式（3），统计崇文门站2号线换5号线的换乘通道内若干次换乘客流分别在各测量点持续的时间及相应的断面客流率，如表4和图8所示。

图6 5号线换2号线的换乘通道各测量点客流量

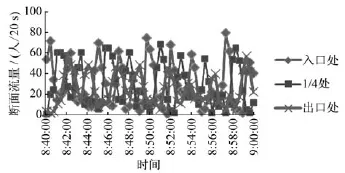
图7 2号线换5号线的换乘通道各测量点客流量

表4 换乘通道各测量点换乘客流平均持续时间

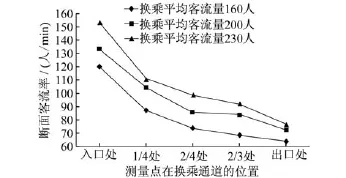
图8 断面客流率与测量点在换乘通道的位置关系

图8 的断面客流率与测量点在换乘通道的位置关系也可看作为断面客流率与换乘通道长度的关系。由图8的实际调研数据分析结果表明：换乘客流量越大，换乘通道内任意一点流率越高；在客流量相同条件下，距离换乘通道入口端越远，该测量点断面的流率就越低。实际调研结果较好地验证了本文提出的客流在换乘通道内的分化规律。

4.2 换乘通道合理长度计算

以崇文门站和复兴门站为例，运用本文所提的换乘通道合理长度的计算方法，并与两站的实际换乘通道长度进行对比。

1）崇文门站的2号线换5号线换乘通道合理长度的计算。站台与换乘通道示意图如图9所示。各可测变量的均值如表5所示。结合式（8），取ρ为0.94 m2（即站台候车区服务水平为B级［8］），换乘通道内v均为1.22 m/s（即换乘通道服务水平为C级［2］），此时计算求得换乘通道合理的最大长度为84 m。即当该换乘通道的长度取84 m时，不仅完全满足缓解客流对站台冲击程度的安全要求，且使站台和换乘通道保持了较高服务水平，与实际的换乘通道长113 m相比，换乘通道长度可缩短25.7%，可降低建设成本和乘客能耗。

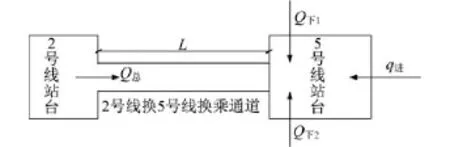
图9 崇文门站2号线换5号线换乘通道示意图

表5 2号线换5号线换乘通道及相关站台调研数据

2）复兴门站1号线换2号线换乘通道合理长度的计算。如图10所示，相同换乘方向有2个换乘通道。此时，计算某一换乘通道的合理长度时，可将另一换乘通道的换乘客流量作为对应站台的下车客流量来看待。实测的统计参数值如表6所示。其他参数取值与崇文门站一致，计算可求得换乘通道1的合理长度为79.5 m，换乘通道2的合理长度为73.3 m。与实际长度相比，分别可缩短7.6%和17.0%。

综上可知，在一定服务水平约束下，以上两例中的实际换乘通道长度的设计偏大。在实际进行换乘通道长度设计时，应根据车站客流预测结果，在满足换乘通道客流安全疏散要求和站台客流承载能力的

基础上，在保证换乘通道和站台的服务水平条件下，进行换乘通道合理长度的确定。

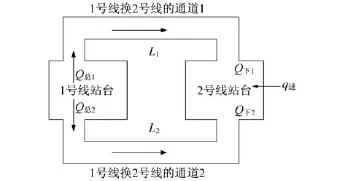
图10 复兴门站1号线换2号线换乘通道换乘示意图

表6 复兴门站1号线换2号线的换乘通道及相关站台调研数据

5 结语

本文通过分析换乘通道长度对换乘客流断面流量的影响机理，提出了换乘通道合理长度的计算方法，并通过仿真试验说明了该方法的有效性。选择北京地铁的2个车站进行了案例研究，通过研究发现，既有车站的换乘通道设置尚有一定优化空间。

［1］ GB 50157—2003地铁设计规范［S］.

［2］ 南海超，胡路，王文谨.地铁车站客流服务水平与通道宽度关系的探讨［J］.铁道勘察，2009（2）：109.

［3］ 蒋阳升，胡路，卢果.基于排队论的地铁人行通道宽度取值方法［J］.交通运输工程学报，2010（3）：67.

［4］ 杜鹏，刘超，刘智丽.地铁通道换乘乘客走行时间规律研究［J］.交通运输系统工程与信息，2009（4）：103.

［5］ Network Rail.Station Capacity Assessment Guidance［R］. London：Network Rail，2011.

［6］ 李得伟，韩宝明.行人交通［M］.北京：人民交通出版社，2012.

［7］ 李得伟.城市轨道交通枢纽乘集散微观仿真理论［D］.北京：北京交通大学，2007.

［8］ 张驰清.城市轨道交通枢纽乘客交通设施服务水平研究［D］.北京：北京交通大学，2007.

［9］ 李三兵.城市轨道交通车站客流特征与服务设施的关系研究［D］.北京：北京交通大学，2009.

［10］ 李三兵，陈峰，李程垒.对地铁站台集散区客流密度与行进速度的关系探讨［J］.城市轨道交通研究，2009（12）：34.

［11］ 吴娇蓉，冯建栋，陆苏刚.通道行人超越行为研究［J］.同济大学学报：自然科学版，2012（2）：228.

Assessment and Calculation of the Rational Length of Transfer Passagewayat Subway Station

Li Dewei，Yin Haodong

The length of transfer passengeway at metro station plays an important role in passengers organization and travel.By referring to the rationality evaluation of transfer passageways'length，and fully considering the differences between passengers，the influencial mechanism of passengeway length over passenger flow is studied，and a simulation analysis is conducted.Based on a case study of Beijing metro passageway between Chongwenmen Station and Fuxingmen Station，an optimum proposal is put forward.In thisstudy，it is discovered that the length and width of metro passageway will decide the passenger flow distribution altogether，while extending the length of passengeway will alleviate the impact of passengers over metro platform，but the length must be controlled in a proper scope.

subway；transfer passageway；rational length；assessment

U 231.4

2013-01-14）

*国家自然科学基金（60674012）；北京市青年英才计划（YETP0555）；中央高校基本科研业务费专项资金项目（2014JBM058）