双连拱隧道中隔墙数值模拟分析

2014-03-23史作璟

陕西理工大学学报(自然科学版) 2014年4期

史作璟

(林同棪国际工程咨询(中国)有限公司轨道事业部，重庆 401121)

随着我国国民经济的快速发展，双连拱隧道作为一种新型大跨度隧道形式，凭借其整体线性流畅、施工占地少、空间利用率高，且双连拱设置避免了洞口道路分幅，并可节省总体工程投资等诸多优点，逐渐得到了工程界的广泛认可。但是双连拱隧道开挖跨度大，左右洞、不同工序相互交错施工对围岩内部应力扰动较大。因此，双连拱三导洞开挖过程中，有必要在设计阶段对作为主要承载结构的中隔墙的应力、位移等进行更加深入的研究。

本文以重庆市高新区森谷路双连拱隧道为工程背景，采用MIDAS GTS 2.6大型有限元软件，对双连拱隧道三导洞台阶法开挖各施工工序进行了数值模拟分析，研究了各阶段施工过程中中隔墙应力及位移变化情况，对施工中可能出现的风险提出了切实可行的处理建议。

1 工程概况

重庆市高新区森谷路南北走向，为城市次干路，设计时速为40 km/h，双向四车道，隧道全长199 m，为短隧道，见图1。隧道最大埋深26 m，洞身采用复合式衬砌，按新奥法原理设计与施工。从受力情况优劣及经济性出发，隧道内轮廓采用曲墙三心圆双连拱断面。隧道所处地区总体呈丘陵斜坡地貌，地形坡度约5°～35°，隧道下穿山脊，上覆土层为第四系粉质粘土，厚约1.0 m左右，下伏基岩为侏罗系中统沙溪庙组泥岩、砂岩层。拟建隧道顶部为丘陵山脊，灌木、杂草丛生，无水体分布，地下水贫乏。

图1 森谷路隧道总平面图

2 计算模型

隧道工程数值模拟，通常采用面单元模拟围岩及隧道开挖体，采用梁单元模拟隧道喷射混凝土及二次衬砌支护，采用植入式桁架模拟锚杆对围岩的加固处理，通过定义单元的“生”或“死”，实现隧道不同工况数值模拟。

根据森古路双连拱隧道实际结构形式及工程地质特征，运用大型有限元软件MIDAS GTS 260建立了适当简化的地层结构法平面计算模型(隧道埋深26 m)。模型两侧及底部取约3倍洞径，上部取到地表。由于模型为平面模型，模型左右边界约束水平方向位移，底部约束竖直方向位移，模型顶部取到地表，为自由边界。模型尺寸为120 m×100 m，网格采用平面四边形单元进行划分，数值分析模型单元划分见图2所示。围岩本构关系采用摩尔-库仑模型，衬砌支护结构采用弹性模型，围岩及支护材料计算参数见表1。双连拱隧道中隔墙受力与稳定与施工步序有密切关系，根据类似工程实践，本隧道施工步序采用三导洞台阶法开挖进行模拟，隧道开挖步序图见图3所示。

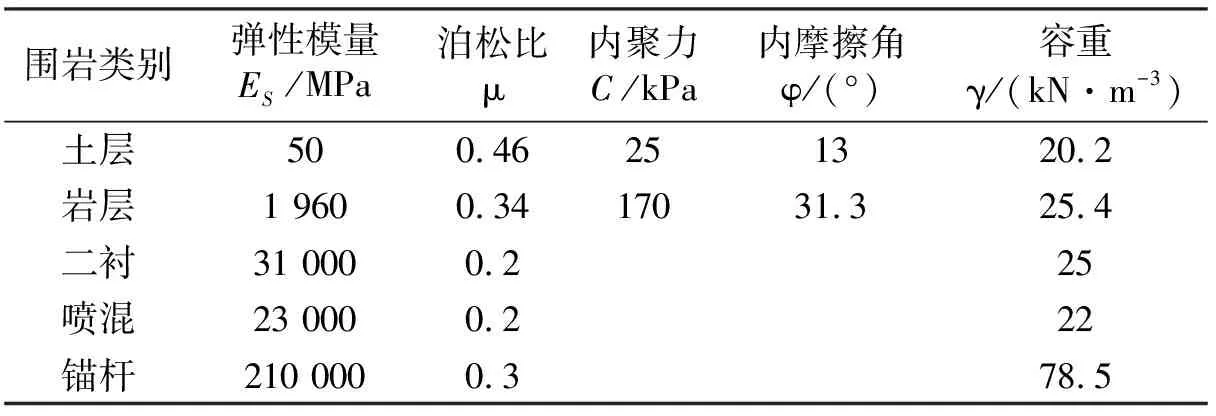
表1 围岩及支护材料计算参数表

图2 数值分析模型单元图3 隧道开挖步序图

3 数值模拟分析

从整个开挖施工步序上来看，双连拱隧道中隔墙及其顶部围岩在施工过程中始终处于扰动状态，中隔墙应力及其竖向位移是最为敏感和复杂的。因此，在设计阶段分析中隔墙应力、位移及其受力变形规律对解析中隔墙失稳机理以及控制施工风险具有重要的现实意义。

3.1 中隔墙应力分析

受到左右导洞开挖及各开挖施工阶段的影响，中隔墙的应力一直处于变化之中，图4为森谷路隧道三导洞台阶法开挖主要施工阶段下中隔墙主应力图。从图中可以看出：中隔墙在浇注完成后其应力场表现为很有规律的对称分布，应力值主要为微小的压力，这也说明中导洞开挖导致了围岩应力重分布，中隔墙浇注完成时其承载力还未完全发挥。随着施工开挖的进行，中隔墙内部应力发生了较大变化，墙体内受压区缩减并趋于集中，墙顶及墙底出现局部受拉区，在整个施工过程中，中隔墙第一主应力呈现出“对称—不对称—对称”分布过程，其产生最大压应力0.95 MPa，顶部产生最大拉应力1.3 MPa，底部产生最大拉应力1.6 MPa(此拉应力为一个比较危险的信号，其已很接近混凝土单轴极限抗拉强度，因此在设计阶段就应该考虑中隔墙顶部及底部可能产生的拉应力)；从不同施工阶段第三主应力图可以看出，开挖施工过程中单侧主洞的开挖无形中会对中隔墙施加一个“偏压荷载”，施工过程中中隔墙一直处于偏压作用下，中隔墙偏压值在左洞开挖完成后达到最大，中隔墙中部左侧轮廓线附近压力约为4.4 MPa，而右侧约为1.5 MPa，压应力变化了约66%，故在施工过程中中隔墙有因偏压而产生扭转的风险，左右主洞开挖完成后，其第三主应力表现为明显的“X”状分布。

Step4 第一主应力图 Step4 第三主应力图

Step6 第一主应力图 Step6 第三主应力图

Step9 第一主应力图 Step9 第三主应力图

Step11 第一主应力图 Step11 第三主应力图图4 不同施工阶段中隔墙主应力图

3.2 中隔墙位移分析

图5为森谷路隧道三导洞台阶法开挖主要施工阶段下中隔墙位移图。

Step4 竖向位移图 Step4 水平位移图

Step9 竖向位移图 Step9 水平位移图

Step11 竖向位移图 Step11 水平位移图

从图中可以看出：随着隧道施工步序的推进，中隔墙水平位移值一直处于变化之中，但总体较微小，极值出现在左洞下台阶开挖后，约0.16 mm；中导洞开挖及中隔墙施做后，中隔墙竖直方向上总体表现为上升，最大竖向位移出现在中隔墙底部，约上升0.4 mm，随着施工阶段的推进，中隔墙竖向位移分布状态与应力分布一致也呈现出“对称—不对称—对称”分布过程，施工过程中先开挖一侧较后开挖一侧对应中隔墙竖向位移大，施工完成后，中隔墙顶部下沉约0.7 mm，底部隆起约0.2 mm。总体来说，施工过程中中隔墙一直处于下沉状态，开挖工况对中隔墙位移影响较小，设计阶段可暂不考虑，中隔墙下沉主要受其下部岩土层地基承载力决定，在设计中可考虑加固地基等措施提高地基承载力，阻止中隔墙下沉。