基于虚拟仪器的动平衡机测量技术研究

2014-03-23江宇飞杨明亮

陕西理工大学学报(自然科学版) 2014年4期

江宇飞，杨明亮

(陕西理工学院机械工程学院，陕西汉中 723000)

0 引言

在各种机械设备中有大量的旋转部件和零件，由于零件结构和材质不均匀等原因，甚至设计时就具有非对称的几何形状等多种因素[1]，导致这些选择件产生静不平衡和动不平衡。随着机械制造水平的迅速提升，设备的运转速度也越来越高，例如早期汽车轮胎一般不进行动平衡检测，而现在汽车轮胎的动平衡已经成了必须检测的指标。现在，企业在加工和制造设备的过程中，对动平衡的要求越来越高，经常有企业到学校咨询并希望对企业研制的产品进行动平衡试验。

动平衡有三点法、影响系数法等，有刚性转子的动平衡和挠性转子的动平衡，有采用动平衡机的动平衡和现场动平衡。近年来，随着虚拟仪器的快速发展，使动平衡测量技术有了很快的进步，但是在动平衡测量中，为了提高测量的效率和精度，还是有许多问题值得研究。如动平衡过程中，有静不平衡量和动不平衡量，各自在动平衡中的影响有多大，对影响系数有何影响，被测试件的质量及分布对动平衡的影响等。

1 测量系统设计

1.1 测量装置

陕西理工学院机械基础实验室有一台型号为DD-300B的动平衡试验机，是1978年由上海试验机厂制造的。当时我国的电子技术水平还停留在电子管时代，测量电路复杂，体积庞大。通过对该动平衡机进行分析，可以采用虚拟仪器技术开发一套测量系统，用于动平衡测量技术的研究。

1.2 DD-300B动平衡试验机

图1为该动平衡机的结构图。在底座7上有两个工件支架1，工件支架上有摆动体10，摆动体上有两个水平放置的支撑滚轮9，被测轴放在两个工件支架的滚轮上，上面通过转子压杆8压住被测试轴。摆动体通过两个摆架簧片11悬挂在工件支架上，显然该动平衡机采用软支撑结构。控制系统通过双速电机5带动万向节头2，带动工件实现两种转速的转动。当转子存在动不平衡时，转子的旋转形成了一个强迫振动，由于摆动体通过簧片悬挂，在水平方向阻尼很小，摆动体就在水平方向产生振动。在每个摆动体上安装有磁电传感器12，运转时传感器出现正弦电信号。

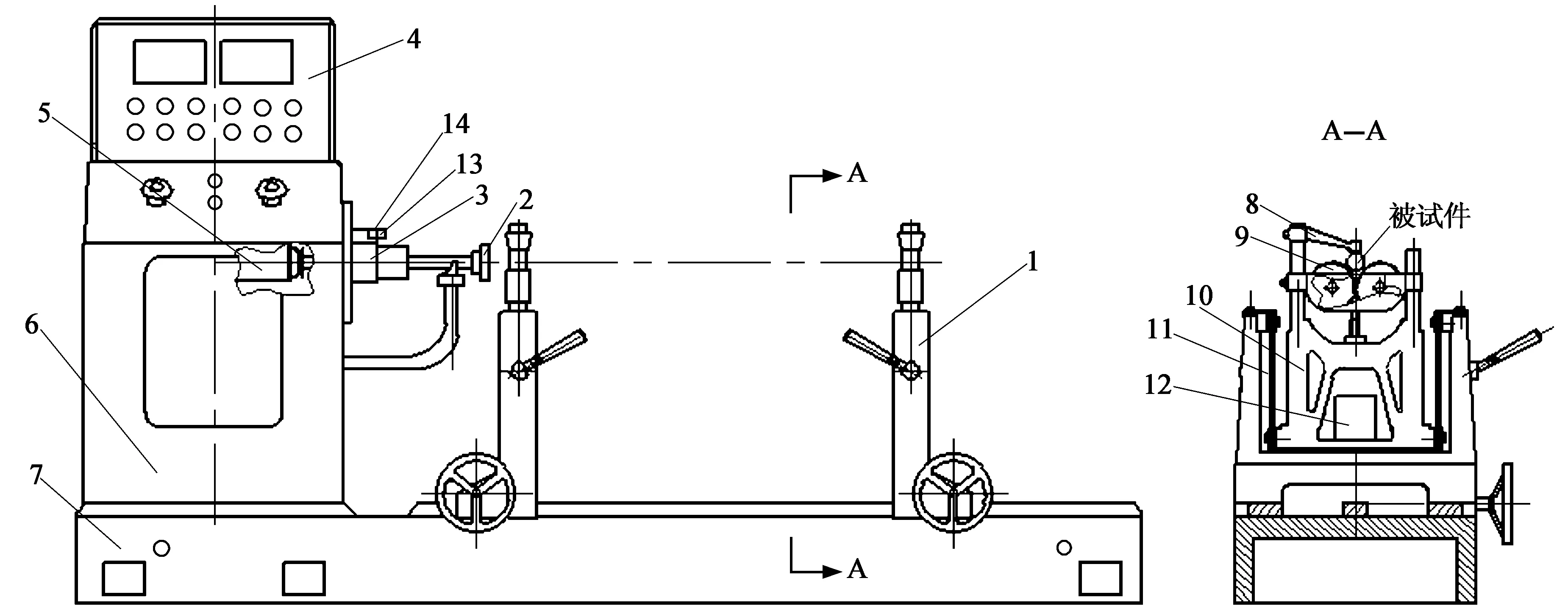
1.工件支架 2.万向节 3.分度盘制动器 4.测量控制箱 5.双速电动机 6.床头箱 7.底座 8.转子压杆 9.转子支撑滚轮 10.摆动体 11.摆架簧片 12.传感器 13.光电开关 14.遮光片图1 DD-300B型动平衡试验机结构图

1.3 动平衡机测量系统设计

1.3.1 测量系统硬件的设计

对转子进行动平衡时，需要在转子的适当位置增加或减少质量，达到消除不平衡力的目的。如果给调整提供一个基准角度零点，就可以实现动平衡的测量与调整。

测量系统采用虚拟仪器技术，用数据采集卡将两路正弦信号采集到计算机中，通过数据处理分离出振动信号的基频信号、振幅和相位。要对转子进行动平衡调整，必须有基准相位信号，因此在改造中增加一个提供基准角度零点的传感器。

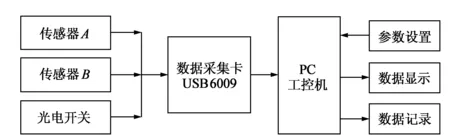
图2 测量系统总体框图

测量系统总体框图如图2所示。该测试系统通过左右摆架上的传感器A和B将摆动架上的振动信号转换为电压信号进入数据采集卡；数据采集卡两路差分输入的模拟信号转换为数字信号；光电开关产生脉冲信号也进入采集卡中，信号进入计算机中，采用LabVIEW软件编程，对信息分析、处理、显示和计算。

数据采集卡选用NI公司的USB-6009数据采集卡，该数据采集卡有8路模拟输入，分辨率为14位，最大采样率为48 kS/s，12路数字I/O口，满足两路模拟信号差分输入和一路数字信号输入的要求。DD-300B型试验机有700 r/m和1 400 r/m两个档位，信号最大频率为23.4 Hz，采样率也满足要求。

基准角相位信号产生装置采用一个槽型光电开关13和一个遮光片14，槽型光电开关的发射器和接收器分别位于U型槽的两边，将光电开关和处理电路安装在分度盘制动器3附近的机箱上，遮光片安装在分度盘制动器附近的转轴上，转子每转一圈，遮光片通过光电开关的U型槽一次，就产生一个脉冲信号，设定脉冲信号下降沿位置就是角度坐标的零点。

1.3.2 测控系统的软件设计

软件设计采用LabVIEW语言，设计的主要内容包括数据采集部分、前面板、数据处理部分和人机对话部分。

图3 动平衡机系统前面板

图3为测量仪器的前面板。前面板能够输出测量信息，同时输入调整信息。调整信息需要人工输入两支点之间的距离、两调整面位置和调整面上施加配重处半径等。数据处理中，主要是振动信号幅值与相位的提取、基准角相位的确定和调整量的优化。

测量系统在处理信号时，是以开始采集数据的点为坐标原点，这就是采集系统确定的角度坐标。由于采集信号的开始位置相对于转子的转角位置是随机的，所以对同一个被测对象，每次得到的信号初相位是不同的。在调整不平衡量时，需要在转子上人为地设置一个角坐标零点，准确知道配重角相位才能进行配重。人为提供的角相位零位，就是遮光片通过光电开关时产生脉冲信号的下降沿。

已知设定的采样率为fs，信号频率为f，则转子每旋动一圈的采样数n=fs/f，每次采样对应的角度θ=360°/n。如果知道光电开关信号下降沿在系统采样坐标中采集的数据量n1，就得到用户角度坐标原点相对系统采样角度坐标原点的位置，也就可以将两路振动信号的采样系统角度坐标转换成用户角度坐标。

利用LabVIEW中“基本电平触发”函数，由输出端“索引”可以得到光电开关信号下降沿在系统采样坐标中采集的数据量n1，信号频率可以由两路振动信号的任一路提取。

2 测量方法研究

2.1 测量方法分析

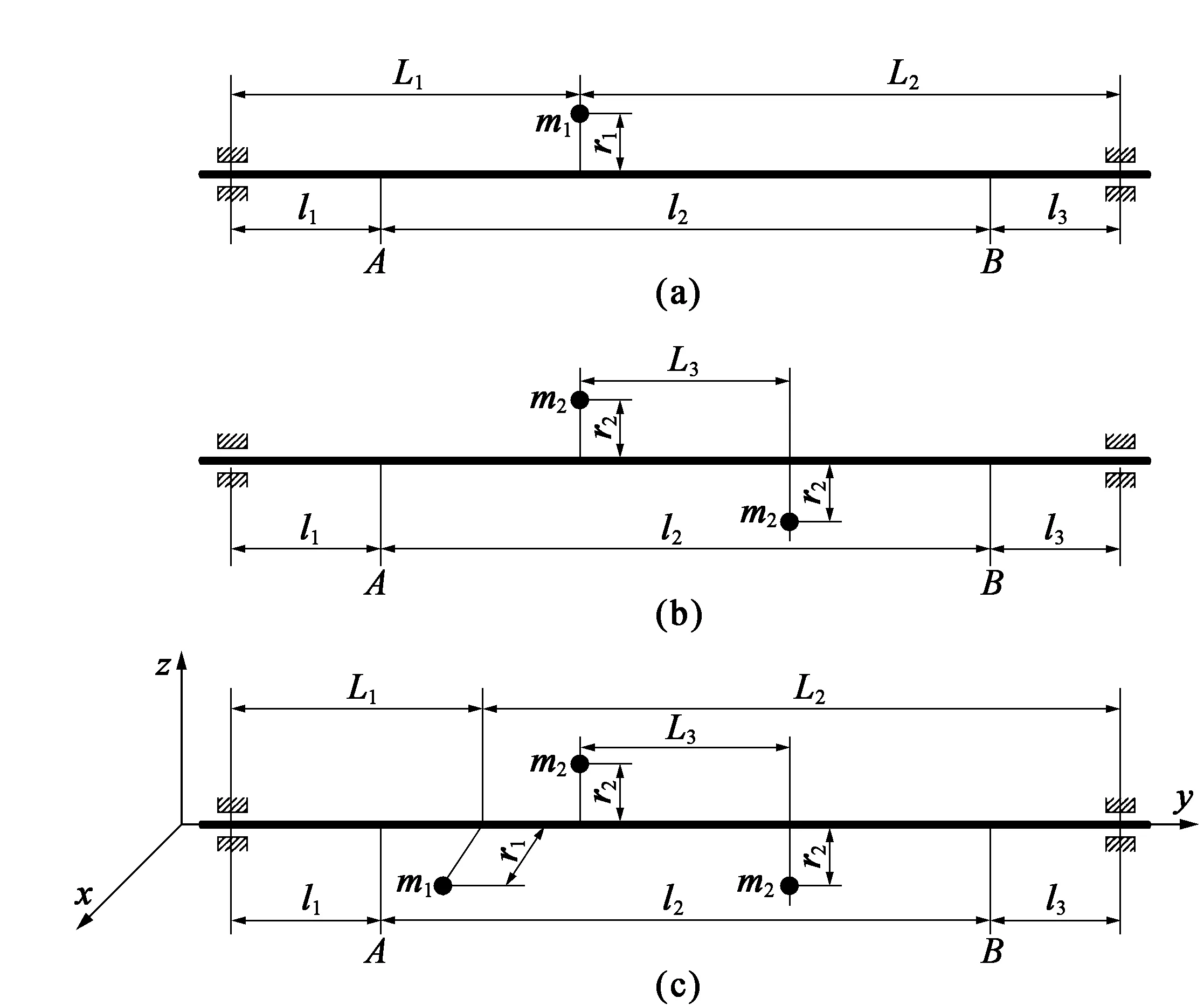
图4 转子平衡示意图

如图4所示，在动平衡中，包含静不平衡、动不平衡和复合不平衡。复合不平衡就是既有静不平衡也有动不平衡，在实际的轴系中，基本上都属于复合不平衡。动平衡研究包含不平衡量的测量和消除。实际测量中，转子同时包含静不平衡和动不平衡，由于转子旋转时形成两种不同的不平衡量，两种不平衡量产生的机理不同，对传感器输出信号影响也不同。因此，有必要将不平衡量中的静不平衡与动不平衡分开，分别研究在复合动不平衡中的影响。

2.2 静不平衡量的测量与消除

静不平衡是沿与轴线正交方向，各偏心质量对轴线取矩之和不为零，设各偏心质量之和可以用一个集中偏心质量等效，如图4(a)所示，转子两个支撑端之间距离为L，作用在距左点为L1的位置上，偏心质量为m1，作用在距转子中心为r1的位置上。

当转子以ω的角速度旋转时，该偏心质量产生的离心力为

FJ1=m1r1ω2。

(1)

该离心力如何分配到两端的支撑处？可以设想，如果该偏心质量力恰好位于两个支撑端的中点，显然对两端的影响是相等的；如果该偏心质量在左支撑端点，应该对右支撑端点没有影响。因此该偏心质量力产生的惯性力可以按力矩平衡原则分配。对左支撑端的作用力为FJL=FJ1L2/L，对右支撑端的作用力为FJR=FJ1L1/L。同样的作用力，不平衡模式对摆动架影响是不同的。对于静不平衡，两个摆动架的摆动方向是一致的，动不平衡两个摆动架摆动的方向刚好相反，因此，设静平衡影响系数为β1，动平衡影响系数为β2。由于两个磁电传感器的灵敏度不同，右端还有万向节联轴器，对摆动也有一定的限制作用，所以两个摆动架的位置对信号幅值也有影响。设左端影响系数为λL，右端影响系数λR。左端传感器输出的电压为UJL=λLβ1FJL，右端传感器输出的电压为UJR=λRβ1FJR。

在进行动平衡时，一般选择两个易于加、减质量的位置进行调整。设在A、B面对该静不平衡量进行调整，增加质量的角度坐标应该在偏心质量对应的180°位置上，定义mr为质径积，则在两个截面上增加的质径积应与原质径积相等，两截面所加质量分别对原质量作用点取矩相等，就可以得到两截面分别增加的质量。

2.3 动不平衡量的测量与消除

动不平衡量的作用结果是在沿轴线方向产生一个转矩。如图4(b)所示，两个质径积m2r2分别作用在相位差为180°、相距L3的轴线上，当转子以角速度ω转动时，离心力产生的转矩为T=m2r2ω2L3。该转矩作用在两个支撑端的作用力FD大小相等，方向相反，计算公式为

FD=m2r2ω2L3/L。

(2)

考虑动平衡影响系数、左端影响系数和右端影响系数，可以得到左端传感器输出的电压为UDL=λLβ2FDL，右端传感器输出的电压为UDR=λRβ2FDR，式中FDL=FDR=FD。

同样，如果要在A、B两个截面进行平衡调整，在与原质径矩M=m2r2L3相反的方向，增加质量和作用半径相等，质径矩等于M，就可以使该转子消除动不平衡力。

2.4 实际转子的不平衡量测量与消除

实际的转子总是静不平衡和动不平衡同时存在的。可以设想，对一个转子经过仔细的静平衡后，转子上只留下动不平衡量。平衡静不平衡量时，可以有无数种方案使静不平衡量为零，但只有满足上述静不平衡量平衡条件的方案，才不会再附加动不平衡量。因此，实际转子的不平衡量，总是可以分解成一个静不平衡量和一个动不平衡量，如图4(c)所示。

由前面的分析可以知道，测量时，获得的信号是静不平衡量和动不平衡量共同作用的结果。一般情况下，静不平衡量与动不平衡量分别作用在不同的角度上，两者之间有夹角α。因此，两个传感器获得电压信号为静不平衡量和动不平衡量的矢量和。

左端传感器输出电压为

(3)

右端传感器输出电压为

(4)

上式中，定义β为无量纲量，则λ的量纲为V/N。

根据两个传感器测量的不平衡量，要在A、B两个端面将转子调整为平衡状态，从理论上讲，第三种状态可以分解为第一种状态和第二种状态，理论上可以在静平衡机上平衡第一种状态，然后在动平衡机上平衡第二种状态。因此，需要在每个调整面上相应位置施加2个平衡块，把两个平衡块进行矢量合成，就得到了合成后的平衡块质量和角度坐标。由于静平衡时，无法准确知道质径积m1r1在转子轴向作用的准确位置，在A、B两个截面上施加配重块就有无数个方案，每个方案附加的动不平衡量是不相同的。根据左右两端测量的振幅和相位，无法直接计算出在A、B两个配重截面上的配重质量和相位。但是，可以通过建立数学模型，给出两个配重截面上配重块质量、角相位与两个传感器输出的关系，数学模型中有4个变量，分别是每个配重面上的配重质量和角相位。让4个变量变化，使配重产生的输出电压抵消两个传感器在测量时得到的电压信号。因此，问题转化为一个优化问题，由于篇幅限制，配重优化研究另文讨论。

3 影响系数研究

3.1 试验方案

在测量系统中，测量结果是无法直接得到转子的静不平衡量和动不平衡量，而只能得到左端传感器和右端传感器分别输出的一个不平衡量总信息。要利用总信息求出两个平衡调整面上调整的质量和角相位，就必须知道公式(3)和(4)中的静平衡影响系数为β1，动平衡影响系数为β2，左端影响系数为λL，右端影响系数λR。

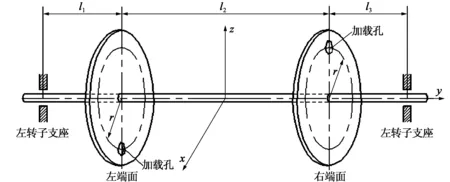
图5 试验转子示意图

为了研究4个系数，设计了图5所示的试验转子，其中l1=l3=60mm，l2=530mm，r=140mm。在该试验转子的两个园盘上相隔180°、半径为r的圆弧上，分别钻了9个孔，使该转子产生了动不平衡量，由于加工误差等，同时还存在静不平衡量。

试验时，首先测出没有加载时两传感器输出的电压信号，再给左端加载盘9个孔的中间一个孔加m的质量，测出两传感器输出的电压信号；然后去掉，又在右端加载盘9个孔的中间一个孔加m的质量，测出两传感器输出的电压信号；利用矢量计算的方法，可以求的得加载质量m对输出电压的影响和相位角的影响。加载后，影响的是静不平衡还是动不平衡量？在左边半径为r处增加了m，则左边的质径积减少了mr，转子上的质径矩减少了mrL2。

每加载一次，对左、右传感器输出都有影响，且施加的静不平衡和动不平衡角相位相同，所以得到两个方程，在左、右两个加载盘上各加载1次，就可以得到如下4个方程：

(5)

(6)

(7)

(8)

通过分析可以知道，在上述方程组中，λR与λL线性相关，β1与β2线性相关。要求解方程组，对(5)—(8)式进行变量代换。分别用x1=λLβ1、x2=λLβ2、x3=λRβ1、x4=λRβ2替换，求解结果如下：

(9)

(10)

(11)

(12)

在以上公式中，x1为静平衡左端影响系数，x2为动平衡左端影响系数，x3为静平衡右端影响系数，x4为动平衡右端影响系数， μ=mrω2/L，UL1和UR1分别为左边加载时左传感器和右传感器输出最大幅值时的电压，UL 2和UR2分别为右边加载时左传感器和右传感器输出最大幅值时的电压。x为影响系数，其物理意义为：在转子不同截面加载的静不平衡力和动不平衡力对两个传感器输出信号的影响，单位为mV/N。

3.2 测量数据处理及分析

按照前述的标定方案，测定该测量系统的系数。首先在没有加载的状态下，对试验转子进行了测量，测量结果为：左端传感器幅值是744.3mV，相位为114.92°，右端传感器幅值是496.58mV，相位为277.13°。理论上左、右加载盘各加载1次，就可以计算出4个影响系数，为了观察影响系数的稳定性，分别加载了4个偏心质量，先在左加载盘加载，测量数据见表1，然后又给右加载盘加载，测量数据见表2。

表1 左端面加载测量计算结果

表2 右端面加载测量计算结果

知道了加载前的信号幅值与相位、加载后的信号幅值与相位，就很容易求得加载的偏心质量对信号幅值的影响，计算的数据见表1和表2。计算时，用到的数据为：L1=60mm，L2=530mm，r=140mm，L=650mm，ω=700r/m。将数据代人公式(9)—(12)，计算的影响系数见表3。

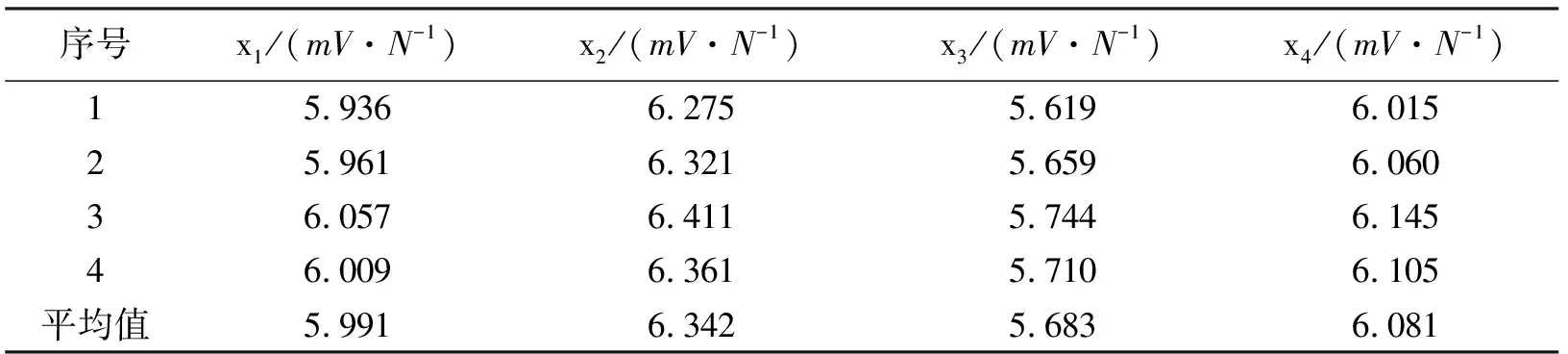
表3 影响系数计算结果

3.3 测量结果分析

由表3看出，4次加载计算得到的影响系数变化都较小，说明试验的稳定性较好。

对影响系数进行分析，x2大于x1，x4大于x3，说明动平衡影响系数大于静平衡影响系数。从表中可以看出，x1大于x3，x2大于x4，即左摆动架的影响系数大于右摆动架的影响系数。

由变量代换关系可以得出静平衡系数与动平衡系数的关系为β1/β2=x1/x2=x3/x4，带入表3中的数据，x1/x2=0.944 6，x3/x4=0.934 5，两个数据相差0.01。从理论上分析，两者应该是相等的，误差估计是由测量误差和数据处理误差引起的。从静平衡系数和动平衡系数的定义可以知道，静平衡系数是将静不平衡的惯性力按静力学方法折算到两个支座上，动平衡系数是将动不平衡惯性力矩按静力学的方法折算到两个支座的作用力。在传统的动平衡分析方法中，两个力大小相等，则对传感器信号幅值的影响也是相等的。通过本次试验发现，虽然静不平衡和动不平衡折算到支座上的力是相等的，但对信号幅值的影响是不同的，动不平衡产生的影响要大于静不平衡的影响。由于影响不同，对平衡配重的要求也不同，直接影响动平衡的精度。产生的原因，需要更进一步的理论研究。

经过数据处理，发现左端影响系数和右端影响系数也是不相同的，左端影响系数大于右端影响系数，λR=0.948 5λL。该系数的不同，除传感器灵敏度影响外，主要是由右端的万向节产生的影响，万向节给被试轴施加了一个作用力，导致振幅减小。