现金管理中的Baumol模型和Miller-Orr模型
2014-03-22吴松华
吴松华
现金管理中的Baumol模型和Miller-Orr模型
吴松华
企业财务管理是对企业资金筹集和运用的管理,其重点是现金管理。现金资产是企业中流动性最强的资产,又是企业中盈利性最低的资产。因此,现金管理除做好日常现金流转控制外,还需要控制好现金持有规模,确定最佳现金持有量。本文将介绍确定最佳现金持有量的两种模型即Baumol模型和Mill-Orr模型,以供企业管理人员参考借鉴。
财务管理;现金管理;Baumol模型;Miller-Orr模型
现金是企业资产中流动性最强的,它具有普遍的可接受性,随时可以有效地进行交易。财务管理上所讲的现金指的使企业的货币资金,因此企业的库存现金、银行存款、见票即付的银行票据等都属于现金的内容。企业为满足日常生产经营,需要持有一定数量的现金,但是现金资产又是企业中盈利性最低的资产,持有现金过多,就会降低企业盈利水平。因此,企业如有多余现金,则常用来购买为有价证券。以控制好现金持有规模,做到最佳现金持有量。有价证券变现能力强,当现金不足需要补充时,就出售有价证券取得现金。这样有价证券就成为了现金的替代品。
下面本文将介绍确定最佳现金持有量的两种模型——Baumol模型和Miller-Orr模型,供企业管理人员参考。
一、Baumol模型
1952年美国经济学家William·Baumol提出了用以确定最佳现金持有量的Baumol模型。
利用Baumol模型确定最佳现金持有量,必须假定以下基本前提:(1)企业的现金流入量是稳定并可预测的。(2)企业的现金流出量是稳定并可预测的。(3)在预测期内,企业不会发生现金短缺,并可以通过出售有价证券来补充现金。在符合以上基本前提下,企业的现金流量可用图1来表示。

在图1中,企业现金需求总量在一定时期内是确定的,企业的最佳现金持有量是N元,在一个周期t内均匀地耗用完,然后出售数量为N元的有价证券来补充现金,以后各个周期不断重复。
现金的持有成本与现金的持有量成正比,现金持有量越大,现金的持有成本就越高。而现金的转换成本则和现金与有价证券的转换次数密切相关,在全年现金需求总量一定情况下,现金持有量越大,现金与有价证券转换次数就越少,所以,现金的转换成本与转换次数成正比,与现金持有量成反比。这样,现金的持有成本与转换成本就呈反方向变化。在现金需求总量一定的情况下,现金持有量越高,其持有成本就越大,而转换成本则越小。因此,两种成本之和最低时的现金持有量就是企业的最佳现金持有量。Baumol模型的最佳现金持有量可用图2表示。
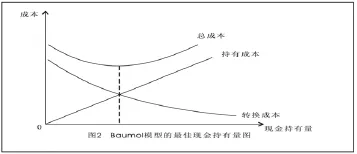
假设:C为现金的总成本;b为现金与有价证券的转换成本;T为一定时期的现金需求总量;N为最佳现金持有量;i为有价证券的利息率。则持有现金的总成本可用如下公式来表示:
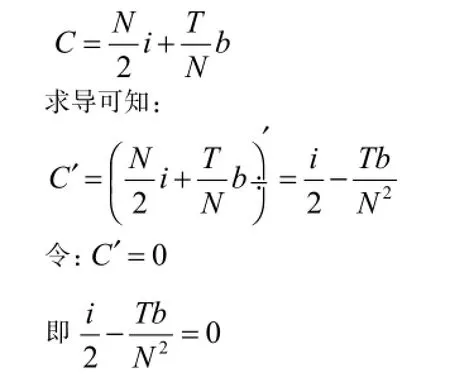
求得最佳现金持有量为:
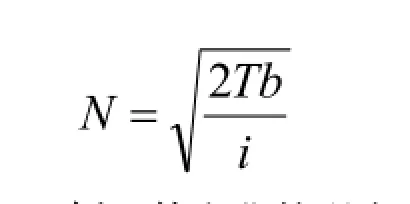
例1.某企业的现金流量稳定,预计全年的现金需求总量为200000元,每次出售有价证券的转换成本为400元,有价证券的年利率为10%。采用Baumol模型确定该企业的最佳现金持有量。
根据Baumol模型的公式,可计算出该企业最佳现金持有量N为:

所以,该企业最佳现金持有量为400000元。
Baumol模型用来确定最佳现金持有量比较简单明了,但是由于其假定现金的流出量稳定不变,实际当中这样的情况很少有。
二、Miller-Orr模型
1966年美国经济学家Merton Miller和Daniel Orr首次创建了一种能在现金流入量和流出量随机波动情况下确定最佳现金持有量的Miller-Orr模型。对企业来讲,现金实际的需求量往往波动大且难以预知,但企业可以依据历史数据和现实情况,测算出一个现金持有量的合理范围,即制定出现金持有量的上、下限,将现金持有量控制在合理范围之内。当现金持有量达到范围上限时,就用现金购买有价证券,使持有量下降;当持有量下降到范围下限时,则将有价证券兑回现金,使现金持有量上升。若现金持有量在上下限合理范围之内,则不必进行相互的转换。这种对现金持有量的控制,可用图3表示:
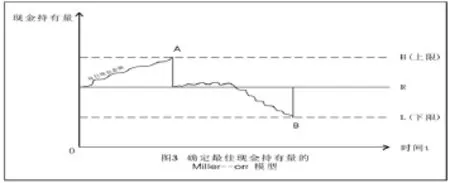
图3中,虚线H为持有量的上限,虚线为L为持有量的下限,实线R为最优现金返回线。从图中可以发现,企业的现金持有量是随机波动起伏的,当其到A点时,即达到控制持有量的上限,此时企业应该购入有价证券,让持有量下降到R线,即现金返回线;当持有量下降至B点时,即达到控制持有量的下限,此时应该出售有价证券取得现金,使其持有量回升至R线的水平。现金持有量在合理控制范围内的上下限之间的波动变化,不需要进行转换。图中的上限H,现金返回线R,可按下
列公式计算:

公式中:b—每次出售有价证券的转换成本;
i—有价证券的月利息率;
σ—预期每日现金余额变化的标准差(可根据历史数据测算)
而下限L则需要根据企业每日的最低现金需要,企业管理者愿意冒缺少现金风险的程度等因素的影响来确定。
例2.假定某企业持有的有价证券为9%的年利率,固定转换成本为每次60元,企业认为在任何时候其银行活期存款及库存现金均不能低于1000元,又根据以往资料测算出现金余额波动的标准差为800元。最优现金返回线R,现金控制上限H的计算如下:
有价证券日利率=9%÷360=0.025%
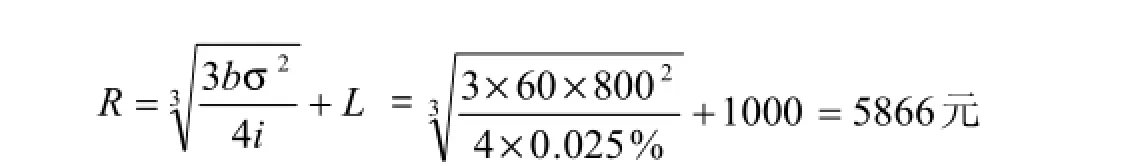
H=3R-2L=3×5866-2×1000=15598
这样,当企业的现金持有量达到15598元时,即应以9732元(15598-5866)的现金去购买有价证券,使持有量下降到5866元;当企业的持有量降至1000元时,则应兑换4866元(5866-1000)的有价证券,使持有量回升到5866元。
Miller-Orr模型建立在企业的现金未来需求总量和收支不可预测的前提下,因此计算出来的现金持有量相对比较保守。
三、结语
以上介绍了Baumol模型和Miller-Orr模型的应用前提、计算公式、计算方法以及优缺点等,随着我国证券市场不断的完善,上述两种模型在企业管理特别是现金管理中将发挥重要作用。
[1](美)詹姆斯·范霍思,约翰·瓦霍维奇.《现代企业财务管理》[M].经济科学出版社.1988年版.
[2](美)斯蒂芬·罗斯,伦道夫·威期特菲尔德.《公司理财》[M].机械工业出版社.2004年版.
[3]汤谷良,王化成主编.《企业财务管理学》[M].经济科学出版社.2000年版.
[4]2012年度注册会计师全国统一考试辅导教材.《财务成本管理》[M].中国财政经济出版社.2012年版.
(作者单位:咸宁职业技术学院)
