基于加权网络的DRFM干扰PD雷达特征研究∗
2014-03-21李云鹏
崔 伟,李云鹏
(空军航空大学信息对抗系,吉林长春130022)
0 引言
新型干扰样式的出现,对现代雷达已经能够造成严重的干扰[1]。基于数字射频存储器(DRFM)的干扰技术[2]是一种现代电子战的前沿技术,通过生成干扰信号与被干扰雷达信号波形匹配达到干扰目的。文献[3-8]对DRFM技术均作了相关研究。其中,文献[3]对线性调频脉冲压缩雷达的DRFM干扰效果进行了探讨,文献[4]对PD雷达速度欺骗干扰进行了分析,文献[5]对高重频信号的DRFM干扰技术研究。但上述研究均未分析干扰信号的波形特性,也未分析被干扰雷达对干扰信号的处理特性。本文主要对基于加权网络的3 bit相位量化DRFM干扰信号特性进行了分析,给出了加权网络的加权值,建立了3 bit相位量化DRFM时域波形表达式,利用仿真分析了3 bit相位量化DRFM干扰信号的频谱特性。针对PD雷达模型的信号处理过程对DRFM干扰效果进行了分析,对研究DRFM的干扰效果以及雷达的抗DRFM干扰都具有重要意义。
1 DRFM的量化方式
数字储频技术总体上可以分为幅度量化方式和相位量化方式两种体制。幅度量化DRFM存储信号时保存了信号的幅、相信息,使重构信号有很高的保真度。但由于自身系统的结构复杂,所以难以实现单片集成DRFM系统。相位量化DRFM虽然仅仅保存了信号的相位信息,但不影响对脉冲雷达的干扰,而且相位量化DRFM的关键器件A/D变换器和D/A变换器易于集成,因此相较幅度量化,相位量化DRFM得到了广泛应用。
相位量化DRFM最主要的量化方式是正交信号比较法,其结构框图如图1所示。其基本原理是基于任意相移的信号都可以通过原信号的正交信号变换而产生。输入射频信号经正交下变频后形成I、Q两路正交信号。这两路正交信号再经相位量化器进行处理形成四路相位相差45°的方波信号,如图2所示。

图1 正交信号比较法相位量化

图2 移相方波信号
它们分别表示为

相位量化器产生的4路方波相当于4位的数字信号,而用4位数字信号表示8个相位区间会有1位的冗余,因此只需要经编码器进行重新编码后产生3位的相位码即可。信号的重构过程与存储过程相反。当需要重构信号时,将存储器中存储的数据读出,经过并串转换器(PISO)恢复串行数据,重构I、I+Q、Q、Q-I四路方波。加权相加网络对重构的方波进行加权相加,产生两路阶梯式正交模拟信号,然后经正交上变频后相加即可得到输出信号。
加权相加网络可以很好地还原出输入信号的外包络,因此,加权值的确定,直接影响了产生干扰信号的特性,为了便于实现,我们利用等均值离散的方法,将时域信号进行模拟等分,利用合成信号来反推各路方波的权值。因此可以通过计算得出当DRFM为3 bit相位量化时,其权值分别为a1=2-2cos(π/4),a2=2cos(π/4),a3=2cos(π/4),a4=2-2cos(π/4)。
这样,我们就可以得到3 bit相位量化DRFM时域波形表达式:

DRFM时域波形图如图3所示。

图3 DRFM时域波形图
2 DRFM干扰信号频谱特性
由于DRFM干扰信号由相位量化产生,因此不可避免地产生寄生信号。寄生信号中影响最大的是谐波性寄生信号[7],一方面,它降低了干扰机的有效辐射功率;另一方面,它可能成为雷达发现和检测目标的信标。由3 bit相位量化输出信号的波形可以看出f(t)的直流分量为0,周期为T,且为偶函数,则可以将f(t)展开成以下形式:

式中,
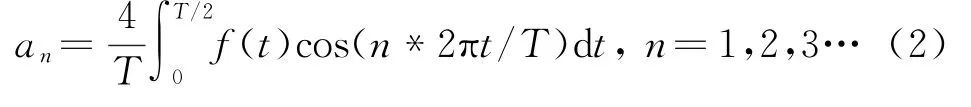
称为f(t)的傅里叶级数的系数。为了便于分析,可以把式(2)改写成:

由于f(t)是偶函数,并且f(t)是奇谐函数,对式(3)括号中的第二个积分项进行变换,可得

整理后可得

将输出波形中的各参数代入式(5),即可得
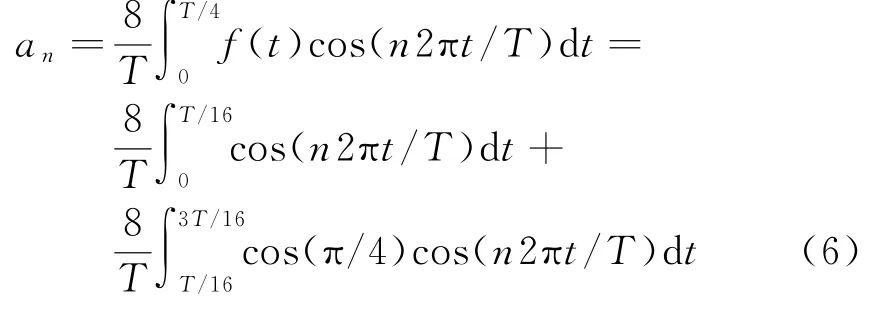
当量化的比特数为m时,输出信号的傅里叶级数为

式中,

当m≥3时,对上式求和,式中的2m-3项(即为中间项)单独列出,并把第1项与第2m-2-l项合并,经整理后可得

利用三角公式可将x n项化简为

式中,k=n-sin(nπ/2)。
当m≥4时,采用与上面相似的方法,可以把上面的式(10)进一步化简成:

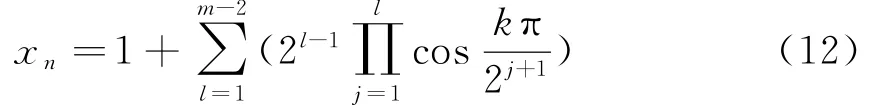
通过上式可以看出,x n是由cos(kπ/4),cos(kπ/8),cos(kπ/16)… 叠加而形成的,可以将x n进一步简化成:

式中,n=1,2m±1,2∗2m±1,3∗2m±1…
将上式回带到通式a n中可得

式中,n=1,2m±1,2∗2m±1,3∗2m±1…
此时得到的a n即为输出信号的傅里叶级数化简后的表达式。1次谐波为信号的固有频率,而高次谐波是寄生信号。若令A n=[a n/a1]表示相对基波信号的寄生信号幅度,则可得到

式中,m为量化位数,m≥2。若以d B为单位,则表示为

式中,n=1,2m±1,2∗2m±1,3∗2m±1…
3 仿真与分析
(1)信号频谱特性
对方波加权相加法产生的信号进行快速傅里叶变换后得到信号的频谱。假设量化比特数m=3,周期T=1,采样频率Fs=1000;根据前面的分析可知,3 bit相位量化输出信号的频谱将在n·2m处产生寄生信号,即F=7,9,15,17,23,25,31…处。从图4由生成的频谱可以看出,阶梯信号的自身频率为F=1,是能量最高的信号。并且在F=7,9,15,17,23,25… 谐波处产生寄生信号。与计算得出的n·2m±1相同。

图4 3 bit相位量化信号频谱图
(2)DRFM干扰信号对PD雷达干扰效果分析
PD雷达的仿真系统主要有正交双通道处理、旁瓣对消、脉冲压缩(匹配滤波)、动目标显示(MTI)、动目标检测(MTD)和恒虚警处理(CFAR)等关键技术,我们以此来分析DRFM的干扰效果。假设雷达主要工作参数如下:τ=5μs,PRI=20 k Hz,SNR=15 d B,雷达中频为1 M Hz,目标相距雷达R=13 km,假设DRFM以最小时间延迟转发干扰信号,雷达信号和干扰信号时域图分别如图5和图6所示,频谱图如图7所示。比较图5和图6可以看出,DFRM量化产生的干扰信号在波形上与雷达脉冲信号十分相似,唯一的差别就是雷达回波和干扰信号的能量大小可能有所不同,对PD雷达而言,从时域上无法区别干扰信号和回波信号。从图7可以看出,产生的干扰信号中频频率与雷达信号的中频频率都为1 MHz,但干扰信号在7 MHz和9 MHz的位置出现了明显的谐波,这与前面的分析是一致的,而这也对未来雷达从频域来识别干扰信号提供了机会。
我们对PD雷达分别进行距离欺骗干扰和速度欺骗干扰,干扰效果分别如图8~10所示。假设目标相距雷达R=13 km,假目标位于11.5 km处,SJR=0 dB,从图8时域波形来看,雷达可以清晰地对假目标进行检测和分析,其中虚脉冲为假目标所在的位置,实脉冲是真实目标的位置。我们知道,PD雷达主要检测目标的多普勒频移实现对速度的测量,假设移动目标的速度为210 m/s,假目标速度为300 m/s,PD雷达进行16次相干积累,雷达工作时PRI=32 k Hz。图9给出了MTI处理后的图像,从图9可以看出,由于假目标也具备了速度信息,在进行MTI处理之后,真目标和假目标被同时检测出来,雷达无法区分真假目标。在进行MTD处理后,图10中在第7、10号滤波器的位置出现了较强的峰值,将其换算成速度,则v1=210 m/s,v2=300 m/s,分别与真假目标的速度一致,也就是说,PD雷达进行MTD处理以后,成功地检测处理两个动目标的速度,而作为干扰方来说,此时速度欺骗干扰达到了干扰的目地。

图5 雷达信号时域波形图

图6 DRFM干扰信号时域波形图

图7 干扰信号和雷达信号频谱分布图

图8 距离欺骗干扰示意图

图9 MTI处理后信号图
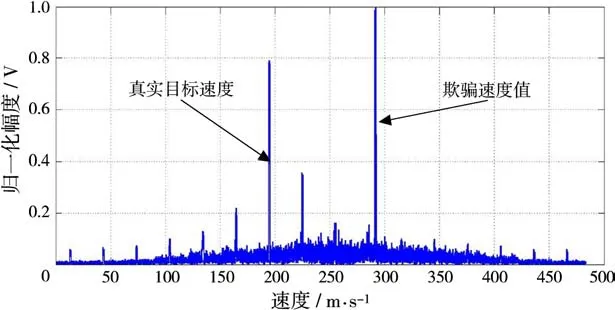
图10 速度欺骗干扰示意图
4 结束语
DRFM技术通过生成干扰信号与被干扰雷达信号波形匹配达到干扰目的,本文主要对基于加权网络的3 bit相位量化DRFM干扰信号特性进行了分析,给出了加权网络的加权值,利用仿真分析了3 bit相位量化DRFM干扰信号的频谱特性。对PD雷达模型的DRFM干扰效果进行了分析,对研究DRFM的干扰效果以及雷达的抗DRFM干扰都具有重要意义。
[1]张崔永,赵风东,杨志祥.新型干扰样式对某型雷达干扰效果研究[J].雷达科学与技术,2013,11(3):241-245.ZHANG Cui-yong,ZHAO Feng-dong,YANG Zhixiang.Research on Jamming Effectiveness of a New Jamming Style to Radar[J].Radar Science and Technology,2013,11(3):241-245.(in Chinese)
[2]董创业.基于DRFM的雷达干扰技术研究[D].西安:西安电子科技大学,2008.
[3]刘忠.基于DRFM的线性调频脉冲压缩雷达干扰新技术[D].长沙:国防科技大学,2006.
[4]王铁,陈波.基于DRFM的PD雷达速度欺骗干扰[J].电子对抗,2006(6):20-22.
[5]王福红.对高重频信号的DRFM干扰技术研究[J].电子科技,2011,24(7):45-47.
[6]李宏,郭雷.单通道DRFM干扰机多目标干扰性能分析[J].电子对抗,2011(4):1-4.
[7]罗金亮,赵静静,张建科.DRFM移频干扰对LFM脉冲压缩雷达的影响及对策研究[J].空间电子技术,2010(2):55-58.
[8]包飞.DRFM系统研究[D].南京:南京理工大学,2006.
