Doppler Shift Estimation of Signals Modulated by Pseudorandom Sequences

Оleg V.Sytnik

(A.Ya.Usikov Institute for Radio Physics and Electronics under the National Academy of Sciences of Ukraine，Kharkov，61085，Ukraine)

0 Introduction

Natural and anthropogenic disasters which are of regular occurrence in different areas of the earth，take a heavy toll of tens of thousands of human lives.It is exactly for this reason that extensive studies are being pursued to design and develop the highly efficient devices for detecting and rescuing the people in the hardest-hit areas.

There are a large number of devices based on different physical concepts.However，the class of radars，especially the hand-held devices，used in rescue operations hold a particular place，because they allow detecting the alive human beings in ruined buildings，under snow avalanches，during sand slides，etc.The operating range of these radars is within 10 to 20 m at a range resolution of～0.5 to 3 m[1-10].

Detecting an alive human being among optically opaque wreckages like brick and concrete walls or snow layer is made possible after analysis of the Doppler modulation of sounding signals reflected from a human body.This modulation brought about by the moving parts of a human body(the motion of limbs，the shifting of a human thorax in breathing and during heartbeat)[10-16].

There are two main trends towards creating the radars with rescue operation functions.One is based on the video pulse location[1-9]and the other is meant to use quasi-continuous pseudo-random signals[10-16].Using the pseudo-random signals the measurement of a distance to a target is accomplished through phase-code-manipulated sounding signals.

Since the main components of the Doppler spectra of data signal lie in the range of～0.1 to 1.5 Hz[12-14]，their measurement against the background of the correlated interferences provided by sounding signal reflection from obstacles，flicker noise，interferences caused by the operation of mechanisms and different-purpose radio-electronics devices is in fact a great challenge.Receiving these signals becomes problematic because the disturbance of the fine(thin)code-sequence structure.Because the thin structure of the code sequence gets disturbed，the coherent reception of such signal becomes somewhat problematic.

In the present paper we have made an attempt to synthesize the structure of the complex phase-code-manipulated signal receiver with noncoherent discriminators to be used in radars for rescue operations.The synthesis is based on the modified non-linear filtering methods.This theory has been used to build the signal processing algorithm.The procedure of synthesis consists of two steps.At the first step we assume that signal frequency has no shift and the base structure of the signal processing algorithm has been obtained.At the second step we assume that the structure of the algorithm remains unchanged and using the theory of signal filtering the filter in the control loop for shifted frequencies is designed.

1 Problem Formulation

Let the realization of an additive mixture of reflected signals and noise arrive at the receiver input

wheres(t)=Ag(t-τ)cos(ωt+φ)is the signal reflected from a target;Ais the signal amplitude;g(t-τ)=±1 is the signal modulation function according to the phase-code-law;τis the reflected signal delay;ωis the radian frequency of a sounding signal;φis the signal random initial phase，which has a uniform distribution on the interval[0，2π];n(t)is the Gaussian noise with zero expectation equal toE{n(t)}=0，(E{·}is the symbol of expectation procedure)and the correlation function:E{n(t1)·n(t2)}=0.5N0δ(t2-t1);N0is the noise spectral density;δ(·)is the delta-function.

The problem is to build an optimal structure of the signal receiving processor to calculate the estimates of parametersωandτusing the observation data(1)and the known signal modulation lawg(t).

2 Optimal Non-Linear Filtering

First，let us assume radian frequencyω，signal phaseφand delayτto be time constants.Then，according to[17]，the differential equation of optimal nonlinear filtering will have the following form:

whereW(t，→λ)is the aposteriori probability density function of the vector of parameters

The aposteriori probability density function for a considered type of signals and under the assumption of Gaussian noise can be given as

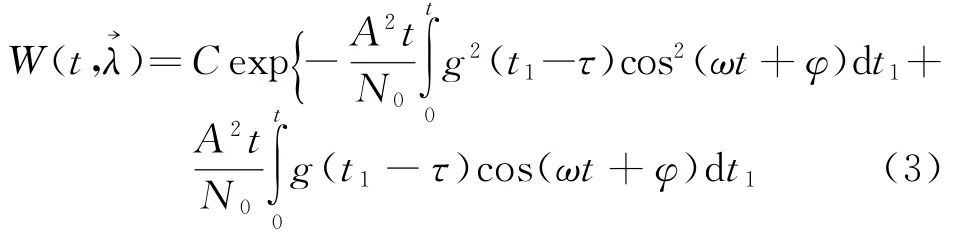
whereCis the constant.

Upon averaging of the left-and right hand parts of equation(2)overφin view of(3)we can write

Since the phase has a uniform distribution in the interval[0，2π]，its probability density function can be given asW(φ)=1/2π.

Then

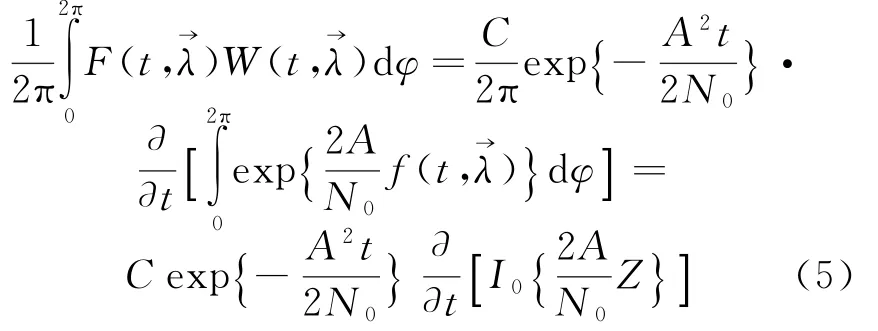
WhereI0{·}is the Bessel function;

Where the central correlated moments，Kωω，Kωτ，Kττform the matrix:

Herewith

The equations for central correlated moments in scalar mode are:

3 Synthesis of Quasi-Optimal Receiver Structure

The solution to a set of equation(10)yields the zero values of coefficientsKωω，Kωτ，Kττfor the stationary case.It indicates that this proce-dure of calculatingKωω，Kωτ，Kττin a stationary mode is unacceptable.It can be easily shown that，with the spectral densityN0of Gaussian noise and the signal amplitudeA，the frequency estimate dispersion is on the order of 12N0/(A2t3).

The time-dependence ofKωωis important in exploring the nonlinear dynamics of the signal frequency tracking system.Simplifying the optimal signal frequency tracking system is feasible if one changes it over to the quasi-optimal mode when the variable coefficients are replaced by constant ones.All this can be done under an obvious assumption that the frequency shifts are too small to get an alive man detected among optically opaque wreckages.As mentioned above，the main components of informative-signal spectrum are within the limits of 0.1 to 1.5 Hz.

The constant amplification coefficients can be derived by averaging the equations overFandKon condition thatt/τi≫1，whereτiis the time during which the parameter with indexiremains practically constant，buttis the current estimation time.In this case，there is no needs to take into account the cross-connectionsKωτ，Kτωbetween the frequency tracking and signal delay tracking networks.They can be taken into account as constant additive factors for amplification coefficients in the appropriate networks.In practice，these coefficients can be obtained by studying the dynamics of information process in training.

Based upon the assumptions that were earlier made，we can turn from partial differential equations to approximate equations，in which the partial derivatives are replaced by finite differences.

wherea=Δωis the frequency increment;b=Δτis the delay increment.

The structure of the device，which implements the frequency(11)and signal delay(12)estimation algorithm is shown in Fig.1.

Fig.1.The structure of the device for adaptive estimation of frequency and delay(Herein the following designations are used:1，2，10，11—multipliers;3，4，12，13—bandpass filters;5，6，14，15—discriminators;7，16—adders;8，17—amplifiers;9—controlled oscillator;18—controlled clock oscillator;19—pseudo-random sequence generator operated by the Mersenne law)

The device incorporates two parallel-connected channels A and B(they are outlined with dashed line in Fig.1)for signal processing as well as the generator 19 of pseudo-random sequences operated by the Mersenne law.Current estimates of the signal carrier frequency and its frequency shift with respect to a sounding signal are calculated in channelА，but in channel B the sequence estimates of signal delay are formed.In contrast to the optimal coherent receiver，the estimates of the signal frequency are calculated by the automatic frequency control networks，but the estimates of the signal delay are calculated by non-coherent discriminator.This design of an adaptive system provides its steady-state operation during large-scale phase and frequency fluctuations.As the sounding signals are being reflected from a human body，the reflected signal frequency fluctuates within a narrow range relative to the con-stant value ofω0because of the slow motion of a human thorax.In other words，we have

It follows from(13)that it is convenient to use the Kalman filter in order to estimate the signal frequency for the stationary mode along with an information model.Then

The difference(ω-^ω)is the output signal of the linearized frequency discriminator the algorithm of which is obtained by means of nonlinear synthesis.

Fig.2 presents the performance characteristics of the proposed receiver as compared to an optimal coherent receiver(a family of curves for adequate-detection probabilityP Das a function of the signal-to-noise ratio“q”at a fixed false-alarm levelP F).As is seen from Fig.2，the signal energy losses resulting from the use of the constant amplification factors in the feedback loop of the frequency estimation channel do not exceed 1.5 to 3 dB.This is well suited for nonlinear data processing with apriori uncertainty in frequency fluctuation probability distribution.

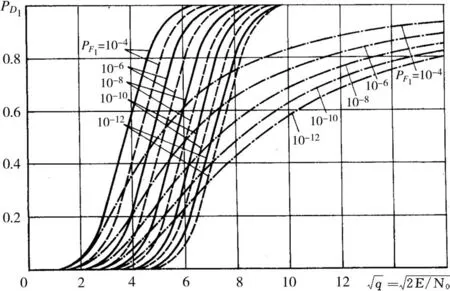
Fig.2 The performance of the quasi-optimal receiver

As evident from the above Figure，the solid lines indicate the operational characteristics of the optimal receiver with no apriori uncertainty of interference distributions.The dashed lines indicate the operational characteristics with apriori uncertainty of the initial phase，and the dash-and-dot lines point to the operational characteristics of the quasi-optimal receiver.

The general view of the radar in which an algorithm for nonlinear quasi-optimal frequency and delay estimation is shown in Fig.3.

Fig.3 The general view of the radar for rescuers

The basic performance characteristics of the radar are listed in Table 1.

Table 1 The basic performance characteristics of the radar

4 Conclusions

To summarize the foregoing，we can state that in a±πstick-slip modulation of the sounding signal phase the Doppler shifts，which result from the chaotic and regular motions of an target，as well as the signal delays are estimated through the adaptive pseudo-coherent correlation processing procedure.The structure of the quasioptimal receiver incorporates two-channel adaptive filters operating in parallel with a phase-synchronized input signal.

Using the proposed approach to synthesizing the receiver structure is governed by the lack of apriori information on the variations in the probability density of initial data generating processes.This gave rise to somewhat complicated calculations and at the same time ensured that the signal processing device could be invariant to a particular type of target motion.In particular，this sort of a receiver responds effectively both to the linear displacements of a target and to its circulations relative to a certain center of masses or to the rotary motion.Based upon the sequence of combined estimates of Doppler shifts and delays one can make an estimate of the target’s motion law.This estimate may well be used as a model in the dynamic Kalman filtering procedure for improving an estimation accuracy.

[1]BUGAYEV A S，VASILIEV I A，IVASHOV S I，et al.Radar Methods of Extracting Breathing and Heartbeat Signals[J].Radiotekhnika and Elektronika，2006，51(10):1224-1239.(in Russian)

[2]BUGAYEV A S，VASILIEV I A，IVASHOV S I，et al.Detection and Remote Diagnostics of the Human Beings Condition Behind Obstacles Using Radar Systems[J].Radiotekhnika，2003(7):42-47.(in Russian).

[3]IMMOREEV I Y，SAMKOV S V.Ultra-Wideband(UWB)Radar for Remote Measuring of Main Parameters of Patient’s Vital Activity[J].Radio Physics and Radio Astronomy，2002，7(4):404-407.

[4]DANIELS D J.Surface-Penetrating Radar[J].Electronics&Communication Engineering Journal，1996，8(4):165-182.

[5]IVASHOV S I，SABLIN V N，VASILYEV I A.Wide-Span Systems of Mine Detection[J].IEEE Aerospace&Electronic Systems Magazine，1999，14(5):6-8.

[6]IVASHOV S I，MAKARENKOV V I，MASTERKOV A V，et al.Remote Control Mine Detection System with GPR and Metal Detector[C]∥Proceedings of the Eighth International Conference on Ground Penetrating Radar，Australia:[s.n.]，2000:36-39.

[7]IVASHOV S I，SABLIN V N，SHEYKO A P，et al.GPR for Detection and Measurement of Filled up Excavations for Forensic Applications[C]∥Proc of the Seventh International Conference on Ground Penetrating Radar，Kansas，USA:[s.n.]，1998:87-89.

[8]VERTIY A A，GAVRILOV SP，VOYNOVSKYY I V，et al.The Millimeter Wave Tomography Application for the Subsurface Imaging[J].International Journal of Infrared and Millimeter Waves，2002，23(10):1413-1444.

[9]SALMAN A O，GAVRILOV S P，VERTIY A A.Subsurface Microwave Imaging by Using Angular Spectrum of Electromagnetic Field[J].Journal of Electromagnetic Waves and Applications，2002，16(11):1511-1529.

[10]SYTNIK O V，VYAZMITINOV I A，MYROSHNYCHENKO Y I.The Special Features of Radar Developments for People Detection under Obstructions[J].Telecommunications and Radio Engineering，2004，61(10):875-885.

[11]奥列格V·西特尼科.探测人体呼吸的多普勒搜救雷达数字信号处理[J].雷达科学与技术，2013，11(2):111-117.SYTNIK O V.Digital Signal Processing in Doppler Radar for Rescuers to Detection of Human Breathing[J].Radar Science and Technology，2013，11(2):111-117.

[12]奥列格V·西特尼科.低多普勒目标识别难题[J].雷达科学与技术，2012，10(1):10-16.SYTNIK O V.Problems of Low Doppler Targets Identification[J].Radar Science and Technology，2012，10(1):10-16.

[13]SYTNIK O V.Doppler Spectra of Human Breathing and Stochastic Models for Their Description[J].Telecommunications and Radio Engineering，2009，68(9):779-788.

[14]SYTNIK O V，VYAZMITINOV I A，MYROSHNYCHENKO Y I，et al.Spectral Selection of Very-Low Frequencies Processes[J].Telecommunications and Radio Engineering，2009，68(2):137-144.

[15]VYAZMITINOV I A，MYROSHNYCHENKO Y I，SYTNIK O V.Results of the Researches of Attenuation of the Energy of Electromagnetic Waves by Optically Non-Transparent Barriers[J].Telecommunications and Radio Engineering，2008，67(12):1033-1050.

[16]SYTNIK O V.Identification of Slow-Moving Targets Outside Optically Opaque Obstacles[J].Telecommunications and Radio Engineering，2007，66(18):1677-1683.

[17]WOODWARD P M.Probability and Information Theory with Applications to Radar[M].New York:Pergamon Press，1953.