En中Finsler-Hadwiger与Euler不等式的改进

陈士龙

(安徽广播影视职业技术学院， 安徽合肥 230011)

1 主要结果

设三角形ABC的三边长分别为a、b、c，则在二维欧氏平面上有著名的 Finsler-Hadwiger 不等式：

(1)

当且仅当三角形ABC为正三角形时等号成立.

在n维欧氏空间En中，文献[1]建立了下面的结果的两个结果

(2)

(3)

等号成立当且仅当单形Ωn为正则单形.

在二维平面上，任意三角形成立如下的著名的不等式：

R≥2r

(4)

等号成立当且仅当三角形为正三角形，这就是二维平面上的Euler不等式.

在n维欧氏空间En中，也有类似的结果，文献[2]将二维Euler不等式推广到n维欧氏空间En，建立了如下的不等式:

R≥nr

(5)

等号成立当且仅当单形为正则单形.

文献[3-5]分别对n维Euler不等式进行了推广，获得了很多加强的结果.本文对n维Finsler-Hadwiger和n维Euler不等式进行了研究，建立了定理1和定理2，得到了比已有结果更强的结果.

定理1对En中n维单形Ωn，成立下面的不等式：

(6)

等号成立当且仅当单形Ωn为正则单形.

定理2对En中n维单形Ωn，成立下面的不等式：

(7)

等号成立当且仅当单形Ωn为正则单形.

2 引理

引理1[6]对En中n维单形Ωn，有

(8)

等号成立当且仅当Ωn为正则单形.

引理2[7]对En中n维单形Ωn，有

(9)

等号成立当且仅当Ωn为正则单形.

引理3[8]对En中n维单形Ωn，有

(10)

等号成立当且仅当Ωn为正则单形.

3 定理的证明

3.1 定理1的证明

(11)

(12)

由式(11)和式(12)可得

(13)

由算术几何平均不等式有

(14)

由式(14)和式(8)可得

(15)

由幂平均不等式可得

(16)

进行如下的变形

(17)

式(17)即化为

(18)

结合式(18)和式(13)可得

(19)

式(19)经过化简可得

(20)

此结果变形就是定理1.

由证明过程可知，上述各式中等号成立当且仅当单形Ωn为正则单形.

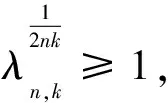
3.2 定理2的证明

由引理2可知

(21)

式(21)与定理1可得

(22)

由式(22)和式(10)，可得定理2，证明过程中的等号成立当且仅当n维单形Ωn为正则单形.

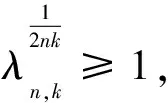
[1] 杨世国.n维Euler不等式的改进[J].哈尔滨工业大学学报，2004,36(6)：781-782.

[2] Borges J, Dougherty S T, Fernandez C C. Characterization and constructions of self-dual codes over Z2x Z4[J]. Adv. Math. Commun,2012,6:287-303.

[3] Fernandez C C, Pujol J, Villanueva M. Z2Z4-linear codes:rank and kernel[J]. Des. Codes Cryptogr,2010,56:43-59.

[4] Yang S G,Wang J.Improvements of n-dimentional Euler inequality[J].Journal of Geometry,1994,51：190-195.

[5] 冷岗松.En中Pedoe不等式的一个加强[J].数学的实践与认识，1995(2)：94-96.

[6] 王文，杨世国.欧氏空间En中Pedoe不等式的推广[J].中国科学技术大学学报，2012，42(11)：913-919.

[7] Mintrinovic D S,Pecaric J E , Volence V. Recent Advances in Geometric Inequalies[M].Dordrecht:Kuwer Acad.Publ.,1989:425-427.

[8] 张景中，杨路.关于质点组的一类几何不等式[J].中国科学技术大学学报，1981，11(2)：1-8.