四轮独立驱动电动汽车转向稳定性的横摆力矩控制

刘 阳， 谢金法

(河南科技大学 车辆与交通工程学院， 河南 洛阳 471003)

汽车的转向稳定性是指汽车能够遵循驾驶者通过转向系统及转向车轮给定的方向行驶，并且当遭遇外界干扰时，汽车能够抵抗干扰而保持稳定行驶的能力[1].四轮独立驱动电动汽车作为一种新颖的驱动形式，不仅可以节约能源、减少排放，在汽车稳定性控制方面也有着很大优势,是当前国际上汽车领域的研究热点.四轮独立驱动电动汽车的驱动系统布置形式中取消了能量源和驱动轮之间的机械传动机构，而由4个电机独立驱动4个驱动轮，同时电机的响应为毫秒级，比传统的内燃机汽车要快得多，只需要根据方向盘转角、制动踏板和加速踏板信号，独立地调节各个轮毂电机的转矩，产生横摆力矩，从而保证汽车的转向稳定性.

国内外对四轮独立驱动电动汽车转向稳定性控制进行了广泛的研究.文献[2]基于模糊控制理论，以横摆角速度为控制变量，调节驱动车轮的驱动转矩；文献[3]提出了一种用于四轮独立驱动的电动汽车的稳定性综合控制方法，该控制系统的上位控制器利用反馈、前馈协调控制方法来确定电动汽车稳定行驶的侧向和横向总控制量，下位控制器利用上位控制器确定的总控制量，采用过自由度控制方法，完成各个马达最优驱动力分配；文献[4]根据四轮独立驱动电动汽车驱动力和制动力矩独立可控的特点，采用层次化结构的控制分配方法优化分配驱动力和制动扭矩来提高车辆的操纵稳定性.本文基于滑模控制理论和模糊控制理论，设计四轮独立驱动电动汽车转向稳定性的横摆力矩控制策略，在Matlab/Simulink环境下选取不同车速、不同路面附着系数进行连续转向行驶和突然转向行驶的仿真分析，以期所设计的控制策略能够将质心侧偏角和横摆角速度控制在稳定范围内，保证汽车转向行驶的稳定性.

1 汽车七自由度模型

1.1 七自由度整车动力学模型

为了进行汽车转向稳定性分析，本文建立了七自由度整车动力学模型，包括汽车的纵向、横向和绕Z轴的横摆运动及车轮的旋转运动.

1)纵向运动

Fyflsinδout-Fyfrsinδin+Fxfl+Fxrr

(1)

2)侧向运动

Fyflcosδout+Fyfrcosδin+Fyrl+Fyrr

(2)

3)横摆运动

0.5d(Fyfrsinδin-Fyflsinδout)-b(Fyrl+Fyrr)+

a(Fxflsinδout+Fxfrsinδin)+0.5d(Fxflcosδout-

Fxfrcosδin)+Fxrl-Fxrr

(3)

4)4个车轮的旋转运动

(4)

5)前轴内外转向轮的转向角

(5)

(6)

式中：m为汽车质量；vx,vy分别为汽车纵向、侧向速度；Iz为汽车绕Z轴的转动惯量；γ为汽车横摆角速度；δ，δin，δout分别为汽车方向盘传递到前轴的前轴转向角、前轴内外转向轮转向角；Fxfl，Fxfr，Fxrl，Fxrr，Fyfl，Fyfr，Fyrl，Fyrr分别为纵向、横向的前左、前右、后左、后右轮胎力分量；a，b分别为前轴、后轴到质心的距离；l为前后轴之间的距离；d为左右车轮的轮距(假设前后车轮轮距相等)；R为车轮的滚动半径；ωij为车轮角速度；Jij为车轮转动惯量；Tbij为车轮的驱动转矩，Fxij为车轮纵向力(以上的i=f,r为前、后轮，j=l,r为左、右轮).

1.2 轮胎模型

1)由于在进行汽车转向稳定控制时，汽车的轮胎长期处于非线性工作区域[5-7]，因此本文选用Dugoff模型.则轮胎的纵向和横向分力分别为

(7)

(8)

式中：Fx为轮胎受到的地面纵向力；Fy为轮胎受到的地面的横向力；Cx，Cy分别为轮胎纵向和侧向刚度；α为车轮的侧偏角；s为轮胎的滑移率；Fz为轮胎垂直载荷.

2)如图1所示，以向右转为例，考虑汽车纵向和横向加速度，则轮胎的垂直载荷分别为

图1 汽车向右转向行驶简图

(9)

(10)

(11)

(12)

3)如图1所示，以向右转为例，各个车轮的轮胎侧偏角分别为

(13)

(14)

(15)

(16)

4)汽车的滑动率用如下式子表示：

(17)

其中各个车轮轮心的纵向速度参照图1向右转向,可以表示为

(18)

(19)

(20)

(21)

式中：s为轮胎纵向滑动率；μ为路面附着系数；Fz为轮胎垂直载荷；α为轮胎侧偏角；a,b分别为前轴、后轴到质心的距离；l为前后轴间距；m为汽车质量；vfl,vfr,vrl,vrr,αfl,αfr,αrl,αrr分别为左前轮、右前轮、左后轮、右后轮的轮心纵向速度、轮胎侧偏角；vx,vy分别为汽车纵向、侧向速度；δ为方向盘传递到前轴的前轴转向角；δout和δin分别为前左、前右车轮的转向角.

2 所需附加横摆力矩的确定及分配

滑模变结构控制是变结构控制系统的一种控制策略，与常规控制的根本区别在于控制的不连续性，其最大特点是在处理包括模型的不确定性和未知干扰在内的不确定因素方面具有很强的鲁棒性和运用性，可实现以简单的控制规律来协调动态和稳定性之间的矛盾.轮毂电机驱动电动汽车转向稳定性控制包含了轮胎侧偏、滑动率及轴荷转移等非线性因素,因此滑模变结构控制在汽车转向稳定性控制方面大有可为[8].

在衡量汽车转向稳定性的因素中，质心侧偏角β和横摆角速度γ是两个重要状态变量[9].转向稳定系控制要能够保持β和γ在稳定范围内.本文基于滑模控制理论，选取β和γ为联合控制变量，根据线性二自由度模型求出转向行驶所需的附加横摆力矩，并以车速和路面附着系数为输入的模糊控制调节β和γ两个控制变量的联合控制参数，实现轮毂电机驱动电动汽车的转向稳定系控制.

2.1 考虑附加横摆力矩的非线性二自由度模型

(22)

b(Fyrl+Fyrr)+Mreq

(23)

式中：Mreq为所需的附加横摆力矩；Fxfl，Fxfr，Fxrl，Fxrr，Fyfl，Fyfr，Fyrl，Fyrr分别为纵向、横向的前左、前右、后左、后右轮胎力分量.

由式(7)、(8)、(22)和(23)建立非线性二自由度模型.

2.2 质心侧偏角和横摆角速度联合控制

由式(22)、(23)可知，质心侧偏角和横摆角速度存在某种耦合关系，以二者为联合控制变量可以解决分别单独控制导致的不能兼顾问题.定义如下滑模面

S=cγ+dβ=0,(c>0,d>0)

(24)

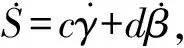
和

根据滑模变结构原理可知，滑模运动到达的条件为

于是得到所需附加横摆力矩为

(25)

式中k为控制参数.由于惯性的缘故，滑模变结构控制不可避免的存在抖振问题，本文主要通过调整控制参数k来控制系统的抖振.前期已经通过仿真确定k大约为70时能基本消除系统的抖振现象.

2.3 联合控制参数c和d的模糊控制

本文以当前车速和路面附着系数为输入，以联合控制参数c和d为输出设计了一种模糊控制器.其中车速的论域为[0,120],模糊子集为{VS(很小),S(小),M(中),B(大),VB(很大)}；路面附着系数的论域为[0,1],模糊子集为{VS,S,M,B,VB}；控制参数的c论域为[1,27],模糊子集为{VS,S,M,B,VB}；控制参数的d论域为[1,27],模糊子集为{VS,S,M,B,VB}.各变量的隶属度函数如图2～图5所示.

模糊控制规则设计的原则如下：

1)车辆在低路面附着系数、低速转向行驶时，控制的主要目的是运动轨迹的保持，对β控制的效果较好，体现在联合控制参数c偏小，d偏大.

2)车辆在高路面附着系数、高速转向行驶时，控制的主要目的是行驶的稳定性，对γ控制的效果较好，体现在联合控制参数c偏大，d偏小.

根据以上原则设计了25条控制规则，c和d控制规则图如图6、图7所示.

本模糊控制选用马丹尼(Mamdani)推理方法进行模糊推理后得到联合控制参数c和d的模糊值， 然后采用重心法求出联合控制参数c和d的清晰值.

图2 车速的隶属度函数图

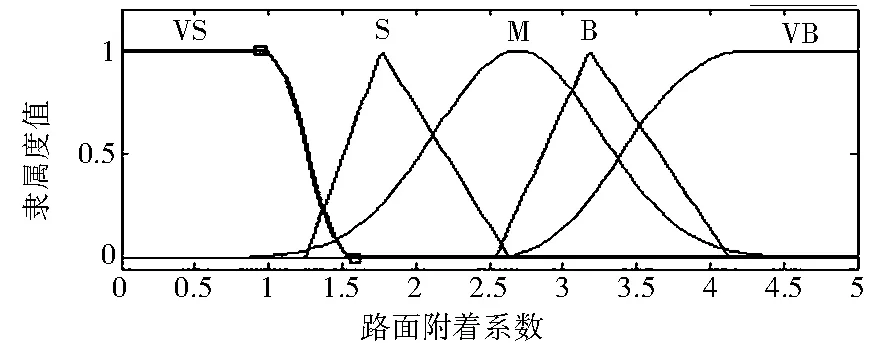
图3 路面附着系数的隶属度函数图

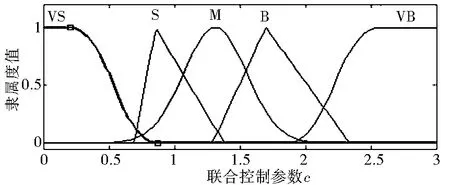
图4 联合控制参数c的隶属度函数图

图5 联合控制参数d的隶属度函数图

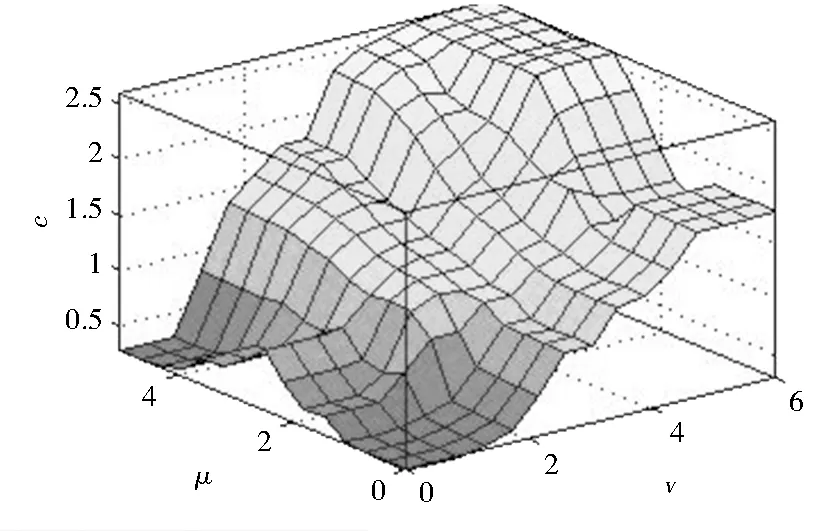
图6 联合控制参数c的控制规则图

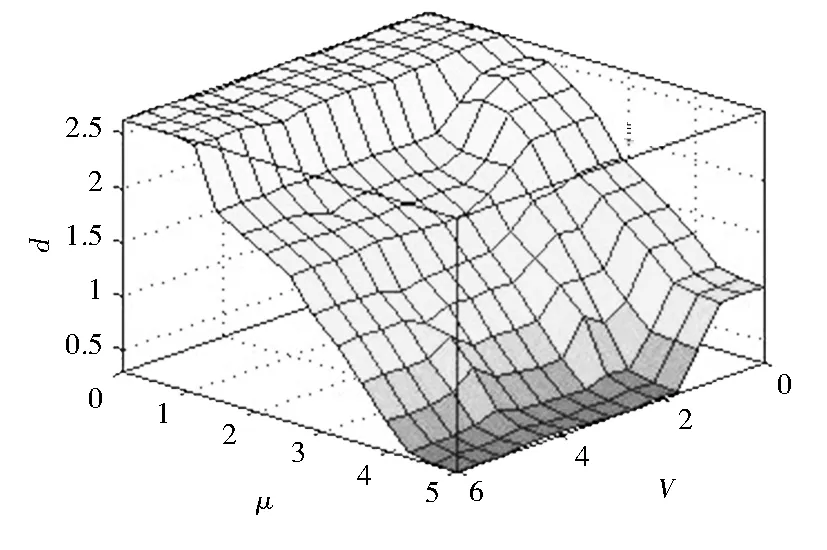
图7 联合控制参数d的控制规则图

2.4 附加横摆力矩的分配

由于前轴两轮参与转向，轮毂电机的效率在低转速、低转矩时偏低，并且轮毂电机可以正转驱动、反转制动，因此以如图1所示向右转向行驶为例，4个轮毂电机的附加转矩分配如下：

(26)

式中：dTbfl、dTbfr、dTbrl、dTbrr分别为前左、前右、后左、后右轮毂电机的附加转矩；参数C的确定与汽车转向角δ有关，本文中δ>0时表示汽车向右转向，δ<0时表示汽车向左转向.

例如，当汽车向右转向行驶时，前轴的轮毂电机的转矩不变，左后轮轮毂电机的转矩增加，右后轮轮毂电机的转矩减小，而这种转矩的变化更有利于汽车向右转向.

3 仿真分析

在Matlab/Simulink环境下搭建如图8所示的轮毂电机驱动电动汽车转向稳定性的横摆力矩控制的整车控制结构图.图9所示为汽车七自由度整车模型，图10所示为轮胎的仿真模型，本论文仿真分析的整车参数见表1.

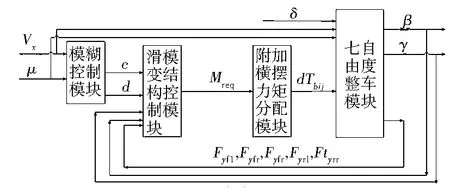
图8 整车机构控制图

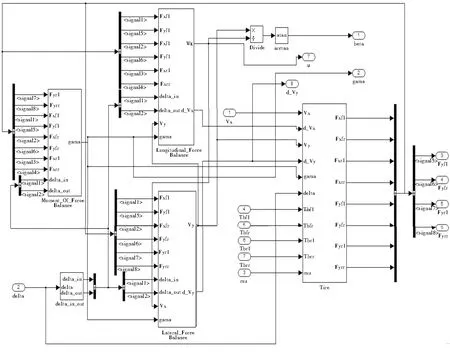
图9 七自由度整车模型

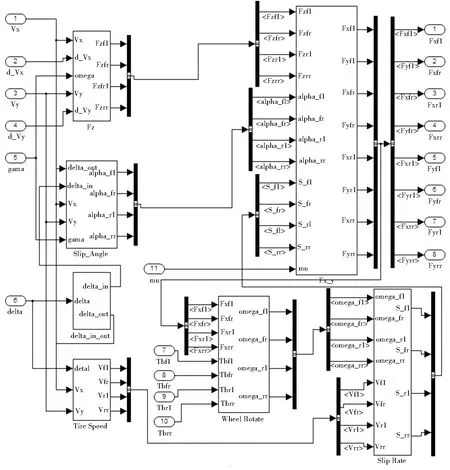
图10 轮胎仿真模型

名称符号数值名称符号数值整车质量/kgm1 100绕Z轴转动惯量/kg·m2Iz1 600质心高度/mhg0.5轮距/md1.4前后轴距/ml2.4前轴到质心距离/ma1.01后轴到质心距离/mb1.31车轮半径/mR0.3车轮转动惯量/kg·m2J11.2轮胎纵向侧偏刚度/N·rad-1Cx-61 762轮胎侧向侧偏刚度/N·rad-1Cy-12 582

1)在路面附着系数μ=0.3，初始车速vx=50km/h，前轴转向角δ=3°sint的情况下进行仿真分析，仿真结果如图11所示.在各个参数响应图中，实线为无滑模变结构模块控制附加转矩的直接横摆力矩控制的变化情况，虚线为有转向稳定性的横摆力矩控制的变化情况(以下皆同).从图11中可以看出，与无滑模变结构模块控制附加转矩的直接横摆力矩控制相比，本论文设计的控制策略的γ和β能够很好地跟踪前轴转向角的变化，并且保持在很小的稳定范围内；ay和所需Mreq都很小，并且变化趋势有所改善，汽车能够实现稳定转向；无滑模变结构模块控制附加转矩的直接横摆力矩控制ay的最大值过大，超出了稳定范围.

2)在路面附着系数μ=0.8，初始车速vx=90km/h，前轴转向角为一幅值为3°的阶跃输入的情况下进行仿真分析，仿真结果如图12所示.从图12中可以看出，相比于无滑模变结构模块控制的直接横摆力矩控制，本论文设计的控制策略的β、γ、ay和Mreq的超调量和幅值均大幅度下降，能够保证车辆转向行驶的稳定性.

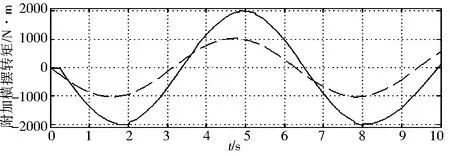
图11 μ=0.3，vx=50km/h，δ=3°sint情况下仿真结果

4 结束语

本文基于滑模控制理论，选取质心侧偏角和横摆角速度为联合控制变量确定了轮毂电机驱动电动汽车转向稳定性所需的附加横摆力矩，并根据轮毂电机效率图的特点对横摆力矩进行了分配.同时，依据车轮在低附着路面、低速转向行驶时，主要控制目的是维持行驶轨迹，而在高附着路面系数、高速转向行驶时，主要控制目的是保证转向行驶的稳定性，基于模糊控制理论，设计了滑模变结构控制的联合参数c和d的模糊控制器.在Matlab/Simu-link环境下，以不同车速和不同路面附着系数验证其在两种典型转向行驶工况下对四轮独立驱动电动汽车转向行驶稳定性的控制效果，并与无滑模变结构模块控制的直接横摆力矩控制进行对比分析，证明了本文设计的转向稳定性的横摆力矩控制在改善汽车转向行驶操作稳定性和防止汽车失稳方面有着明显的优势.

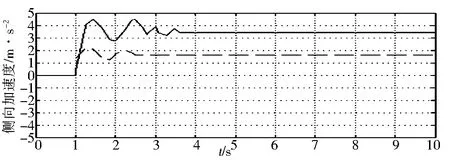
图12 μ=0.8，vx=90km/h，δ=3°(t=1s)情况下仿真结果图

[1] 余志生, 夏群生, 伦景光，等. 汽车理论[M].4版.北京:机械工业出版社，2006.

[2]TahamiF,KazemiR,FarhanghiS.Anoveldriverassiststabilitysystemforall-wheel-driveelectricvehicles[J].IEEETransactionsonVehicularTechnology, 2003, 52(3):683-692.

[3] 贺鹏,堀洋一.四轮独立驱动电动汽车的稳定性控制及其最优动力分配法[J].河北工业大学学报,2007(4):26-32.

[4] 朱绍中,姜炜, 余卓平，等.基于控制分配的轮毂电机驱动电动车稳定性控制仿真研究[J].系统仿真学报,2008(18):4 840-4 842.

[5] 赵艳娥,张建武. 基于滑模控制的四轮驱动电动汽车稳定性控制[J].上海交通大学学报,2009,43(10):1 526-1 530.

[6] 杨化方.基于滑模变结构控制的电动汽车稳定性控制系统研究[D].淄博：山东理工大学，2009.

[7] 张金柱,张洪田,孙远涛.电动汽车稳定性的横摆力矩控制[J].电机与控制学报，2012(6):75-80.

[8] 靳彪,张欣,杨庆保.纯电动汽车低速转向差速控制模型[J].北京交通大学学报，2013,37(4):158-161.

[9] 周翠玉,路春光,李成群.双轮毂驱动电动汽车电子差速控制的研究[J].机械工程与自动化，2013(3)：46-47，50.