基于三维激光扫描数据的不规则实体表面积和体积计算方法

郭景仁， 王艳林， 于 蕾

(中国人民解放军61175部队， 山东淄博 255020)

地面激光扫描，简称TLS(Terrestrial laser scanning),是一种允许数字采集并通过点云在三维空间中以数字形式再现真实物体的技术.激光扫描操作的主要原理是基于作为目标本身的表面反射的激光脉冲传输到目标和分析返回脉冲[1-2].地面三维激光扫描仪的发展和应用，为人们获取丰富的局部地面空间信息提供了一种全新的技术手段，它是一种非接触式主动测量系统，可进行大面积高密度空间三维数据的采集，具有测量点位精度高、采集空间点的密度大、速度快等特点[3].地面三维激光扫描技术的应用为解决土方量计算的空间三维数据采集，提高土方量计算精度提供了有效的方法，土方工程是土地整理的主要项目之一, 其主要目的是通过填挖土方使平整地块的平面位置和高程满足设计要求[4].

目前土方量计算的常用方法有DTM法，方格网法，等高线法，平均高程法和断面法.DTM模型计算的土方量精度相对较高，它是根据实地测定的地面点坐标和设计高程计算得到土方量，测量点的数量及其精度决定了土方量计算的精度，但是数据点越多，占用内存越大，不适合大范围土方的计算[5].方格网法是一种基于栅格的解决方法, 其特点是数据结构和数学模型简单, 易于程序实现, 但格网间距的大小直接影响着计算精度, 而对于复杂地形很难确定合适的格网间距.因此, 计算结果往往与现实情况出入较大, 不能满足实际应用的需要[6].平均高程法操作比较简便，但是该方法误差较大.等高线法的工作内容与步骤和方格法大致相同，不同之处在于计算场地平均高程的方法，它适合地面起伏较大、坡度变化较多时采用.断面法只需要知道两端横断面的面积，因而计算很简单．但如果施工场地范围很大，那么求面积工作量将会非常大，而且容易出错，同时大量的数据容易在计算时带来较大的误差，特别是地形较复杂时，算出的面积值误差会很大[7].

以上介绍的这四种土方量计算的方法，都有其缺点，为了进一步提高土方量解算精度，简化土方量计算的工作程序，满足土方量计算的实际应用要求，现提出有限元的思想.

1 有限元体积及表面积计算原理

任何立方结构都可以通过数学解剖模型分解为有限个体积元.对于土方工程量计算来说，可以先对该土方填挖处进行三维激光地面扫描，利用IDL软件构建三维立体模型.三维实体重构的首要任务是将测量数据按实物原型的几何特征进行分割成不同的数据块, 使得位于同一数据块内的数据点可以用一张特定的曲面来表示, 然后针对不同数据块采用不同的曲面建构方案进行曲面重建, 最后将这些曲面块拼接成实体[8].将重建后的曲面实体进行数学有限元积分，求出其精确的表面面积[9-10].再将此立体模型根据实际地形分布划分为有限个体积元，分析每个体积元中的土方分布，从而计算其土方量.

1.1 有限元体积计算

1.1.1 有限元体积计算原理

将复杂实体三维空间划分为有限个体积大小相同的立方元(图1).利用积分原理，先拟合出所求立方元外部曲面并根据曲面上已知点云数据计算该曲面法线向量，再利用柱面积分原理计算体积.在一定范围内，分割的立方元体积越小，得出的体积精度越高.

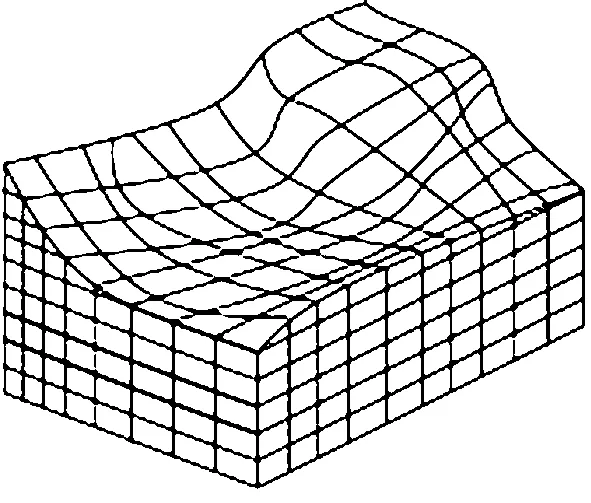
图1 三维立体结构有限元分割图

用有限元思想解算扫描实体模型土石方量的步骤为：

(1)根据点云数据计算空间直角坐标系X轴方向的最大值Xmax和最小值Xmin，Y轴方向的最大值Ymax和最小值Ymin.

(2)如图2所示，将模拟大点云分割为形状、大小相等的有限个虚拟的小立方元，对单个立方元建立空间直角坐标系o-xyz，x′轴、y′轴、z′轴分别与x轴、y轴、z轴平行.

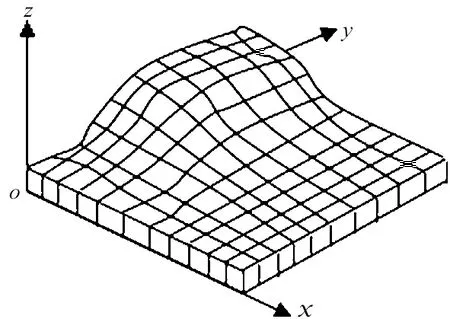
图2 立方元分割示意图

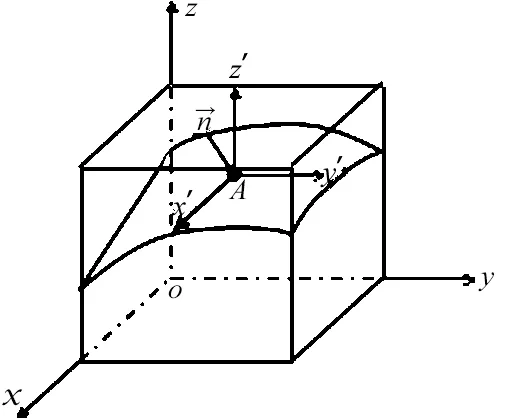
图3 立方元法向量示意图

(3)对该立方元内曲面下的区域进行双重积分求体积.

1.1.2 曲面拟合

曲线曲面拟合是一种古老而常用的技术，在工程、实验、统计和计算机图形等方面有着广泛的应用[11].建立最佳的拟合参数, 运用最小二乘法对其进行曲面拟合, 通过线性变换精确解出控制点的坐标值[12].拟合的基本思路为先选择基本反映曲面形状而且分布均匀的数据点,利用曲面蒙皮技术[13]生成一个基本反映型面形状而且性态良好的曲面,称之为初始曲面.然后以某种映射关系找到数据点在初始曲面上的对应点,并把该点的参数值称为数据点在初始曲面上的参数值,同时建立超定线性方程组.最后利用最小二乘法求解超定线性方程组,得到数据点的最佳拟合曲面[14].本文中我们给出三种基本曲面拟合原理公式，其中法向矢量均以z轴方向为例.

十参数曲面拟合原理[10]的二次曲面方程为

Ax2+By2+Cz2+D+

Exy+Fxz+Gx+Hyz+Jy+Kz=0

(1)

三维空间R3法向矢量为

(2)

其中：

根据法向量与三个坐标轴之间的夹角，选择式(3)或式(4)中的简化方程.双曲面S上的点表示为S={Pk}⊂R3,k=1,2,…，n,k点满足方程：

Sx⊂R3:xk-A-Byk-Czk-Dykzk=0

(3a)

Sy⊂R3:yk-A-Bxk-Czk-Dxkzk=0

(3b)

Sz⊂R3:zk-A-Bxk-Cyk-Dxkzk=0

(3c)

地面平坦时用(3c)，陡峭地方用(3a)或(3b)拟合.当为二次抛物面拟合时，用如下方程：

x-A-By-Cz-Dy2-Ez2-Fyz=0

(4a)

y-A-Bx-Cz-Dx2-Ez2-Fxz=0

(4b)

z-A-Bx-Cy-Dx2-Ey2-Fxy=0

(4c)

上式使用原理同式(3)所述，首先判断法向量与各轴之间的夹角.如当法向量与x轴之间的夹角较小时，在下一步积分时就应该使用关于x轴的方向矢量.

1.1.3 几种体积计算方法

以沿z方向上积分为例，给出几种体积积分公式

(1)十参数拟合曲面体积积分公式：

Fxz+Gx+Hyz+Jy+Kz)dxdy=

(Cz2+D+Kz)(x2-x1)(y2-y1)+

(5)

(2)四参数拟合曲面体积积分公式：

A(x2-x1)(y2-y1)+

(6)

(3)六参数拟合曲面体积积分公式：

Dx2+Ey2+Fxy)dxdy=

A(x2-x1)(y2-y1)+

(7)

其中Ω代表实体体积，公式中x2、x1分别为空间直角坐标系x轴方向的最大值和最小值，y2、y1分别为空间直角坐标系y轴方向的最大值和最小值.

1.2 有限元表面积计算

曲面积分可以看做是无限个子区域的平面积分，即为有限元数学积分原理.

有限元表面积计算与Bézier曲面面积计算原理相似.令Bézier曲面面积为S,分割后得到多个小的曲面片,设第i个小曲面片的面积为Si.由曲面分割过程知,原Bézier曲面经过1次分割后得到4个曲面片,经过2次分割得到16个曲面片,一直进行下去,经过k次分割后可得到4k个曲面片[9]，如图4所示.

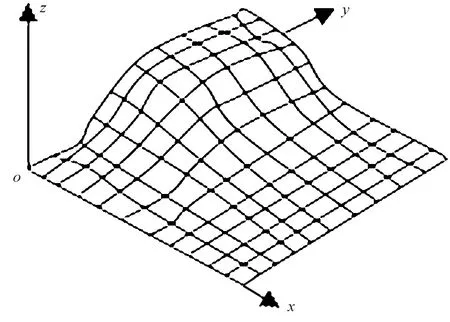
图4 曲面有限元分割

有限元表面面积计算公式：

(8)

SΔij为k次分割后得到的第i个曲面片的控制多面体中第j个三角形的面积.

2 实验及分析

2.1 实验模型及数据介绍

本实验数据为不同的分辨率(相邻两个扫描点之间的距离)点云数据组成的半球，半径为10m.表1是不同的分辨率下模拟半球对应的点个数.

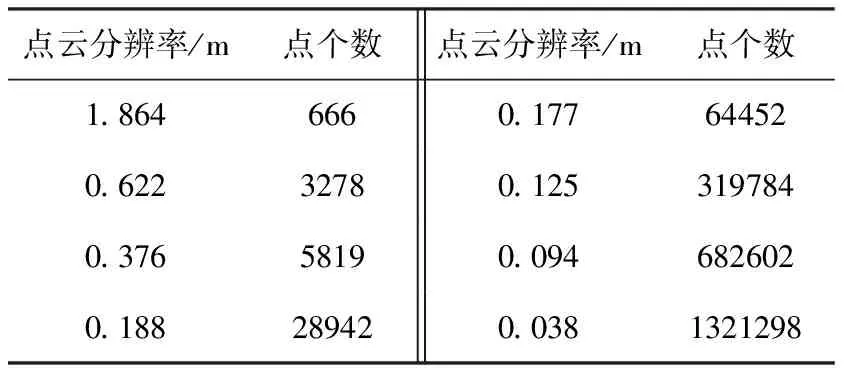
表1 不同的分辨率下模拟半球对应的点个数

模拟的半球如图5所示，半球点个数约130万、分辨率为0.038m,数据处理采用IDL语言开发的基于激光点云的EEXLT(地图要素提取)软件.该实验默认坐标系为空间直角坐标系，各轴之间的位置要求符合右手法则.

本实验中设定的有限元单位立方元长0.2m、宽0.2m、高0.2m.

图5 半球模型

2.2 结果分析

以分辨率为0.038m的半球模型为例，说明本方法的可行性.表2为分辨率0.038m的半球模型的部分点云数据，其高程起算点为零点，建立坐标系原点为(0,0,0)，既以X轴、Y轴所在的平面为起算平面.将模拟半球大点云按长0.2m、宽0.2m、高0.2m的有限元单位立方元分割，得到约2万个单位立方元，表3为部分小立方元内的点个数及体积.

表3 分辨率为0.038m的模拟半球部分小立方元内的点个数及体积

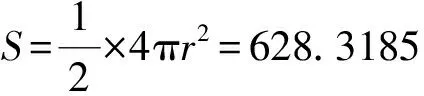
表4 有限元思想解算不同分辨率下半径为10m的模拟半球的体积、表面积及相对误差

相对误差计算公式如下：

(9)

2.3 有限元体积计算精度评定

有限元法体积和表面积计算的精度用相对误差来评定，见图6.

由图6可以看出，点云扫描分辨率越高，体积和面积的计算结果越精确.图7可以看出，模型点云总数越多，体积相对误差越小，结果越精确.表5为分别用等高线法、DTM法、格网法、断面法及有限元法计算分辨率为0.038m的模型体积的结果与精度对比.

图6 不同分辨率下体积和表面积相对误差

图7 不同分辨率下点云总数的模型体积相对误差

计算方法所求体积/m3体积相对误差/%有限元法2094.3511/240000等高线法1471.9151/3DTM法2105.31/40格网法2075.01/100断面法2106.9511/40

显然，相对于其它已知方法，有限元法大大提高了实体模型体积的求解精度，为工程预算提供了可靠的数据.

3 结论与展望

(1)本文提出的有限元法计算不规则实体的表面积和体积是通过有限元积分将其划分为足够小的区域，根据无限逼近的方法进行解求实体的表面积和体积.

(2)有限元法所分得不规则实体的体积元与点云获取的分辨率大小有密切的关系，分辨率越大，其体积元就越小，计算的体积就越精确，反之亦然.

(3)有限元法计算的体积比等高线法、DTM法、格网法、断面法的精度要高几个数量级.

(4)影响有限元积分法计算体积精度的因素为：拟合面上点的个数及分割立方元的大小.所以应用有限元积分原理计算体积时，应首先利用三维激光扫描仪正确并充分扫描得到实体表面无噪声点云数据，并根据实体实际情况划分合适的有限元.

(5)三维激光扫描得到的点云数据必须能够覆盖整个实体表面，点云数据在使用之前必须去除噪音点.在进行曲面拟合，获取曲面参数的时候必须保证有足够多的点云落在该拟合曲面上.

(6)在有限元分割时依据实际情况将实体分割为尽可能小的立方元，以便于进一步提高体积计算的精度.

(7)有限元积分法用于计算工程土石方量，不同实体参数下的曲面拟合，有限元分割有较大差异，具体的分类方法还需进一步研究.

[1] Casula G,Mora P,Bianchi M G. Detection of terrain morphologic features using GPS, TLS, and land surveys:“ttana della volpe” blind valley case study[J]. Journal of Surveying Engineering， 2009,136(3):132-138.

[2] Pirotti F,Guarnieri A,Vettore A.Ground filtering and vegetation mapping using multi-return terrestrial laser scanning[J].ISPRS Journal of Photogrammetry and Remote Sensing,2013,76:56-63.

[3] 朱清海,黄承亮,李凯.基于EPS 2008及地面三维激光扫描点云数据进行断面线提取[J].城市勘测,2013(2):89-91.

[4] 王晓莉，王琳琳.工程土方量计算中土方量精度与DEM分辨率的关系[J].科技情报开发与经济，2007,17(7):191-192.

[5] 胡奎.三维激光扫描在土方计算中的应用[J].矿山测量，2013,(1):71-72.

[6] 杨友长，景妮.构TIN法填挖方计算方法研究[J].金属矿山.2008(7):88-91.

[7] 刘鸿剑，肖伟红.基于DEM的工程土方量算法研究[J].江西理工大学报，2009,30(4):18-21.

[8] 胡敏捷,阎利,张毅.三维激光扫描技术在大型舱容测量中的应用研究[J].船舶设计通讯讯,2011(1):60-64.

[9] 王胜兵,戴明强,黄登斌.基于双线性插值拟合的山形曲面面积计算[J].兵工自动化, 2012, 3(3): 42-43.

[10] 曹俊,陈普春,徐莹,等.基于断层扫描思想的曲面面积计算方法研究[J].现代电子技术, 2012, 35(6): 131-133.

[11] 何芳.移动曲面拟合法在复杂曲面造型中的研究与应用[D].武汉:武汉理工大学, 2008.

[12] 李二涛,张国煊,曾虹.基于最小二乘的曲面拟合算法研究 [J][J].杭州电子科技大学学报, 2009, 29(2): 48-51.

[13] 李玉梅.基于三次 B样条的曲线、曲面逼近算法的研究[D].南京:南京信息工程大学, 2013.

[14] 吴小刚.几何造型技术中逆向柔性曲面重构技术研究[D].成都：电子科技大学, 2012.