基于Contourlet变换和PCA的人脸识别算法

张锦华，孙 挺

（周口师范学院 计算机科学与技术学院，河南 周口466001）

人脸识别是通过提取人脸的相关特征信息进行身份识别的生物识别技术，在智能人机交互、身份鉴别、身份证明、刑侦破案和安全监控等方面有着广泛的应用［1]，近年来取得了较大的进展，涌现出了众多人脸识别算法.然而，在实际人脸识别应用中，大部分算法对光照、姿态的变化均十分敏感.根据国际人脸识别评估报告［2]，在复杂的光照和姿态条件影响下，目前常用的人脸识别算法的识别率约降低14%左右.因此，降低光照和姿态影响是提高人脸识别率的一个重要途径，受到越来越多学者的关注，各种处理方法也陆续被提了出来.目前，效果较好的有基于朗伯光照模型的Retinex、多尺度人脸结构表达方法（multiscale facial structure，MFSR）和多尺度几何分析方法等［3].其中，Retinex方法是在传统的傅氏频域中用原始图像点除其低通图像来获得光照不变量.这种方法缺少多尺度分析能力，不能较好地保留图像在低频光照区域的锐利边缘.MFSR方法加入提高多分辨能力的小波变换，其提取的多尺度空间图像识别率较Retinex方法高.但由于小波变换仅具有水平、垂直和45°三个方向的表示能力，在图像的奇异结构处会产生较多的小波系数，导致对高维信号的表示能力不足.因此，相继有学者提出了Contourlet，Bandelet和Directionlet等一系列多尺度几何分析方法.这些方法具有各向异性和多种方向选择性，能够更有效地捕捉和表示图像的局部特征，尤其是具有线性奇异和曲线奇异等更高维的几何特征，对于图像的特征提取具有重要意义.如Li Yibo等［4]运用Contourlet变换研究了一种新的多尺度角点检测算法，该算法解决了原始角点信息丢失、角点位置偏移等问题.Dong Yongsheng等［5]运用Contourlet子带聚类方法研究了纹理分类相关问题，证明多尺度几何分析方法用于特征提取具有明显的优势.Mosleh A等［6]用高斯模型逼近描述Contourlet子带系数，提取各个子带系数的均值、方差、最大值和最小值来合成特征向量，并应用于图像纹理检索相关问题.但这些方法仅针对Contourlet分解后的高频LCBP系数进行建模，对于Contourlet的低频信息并未加以利用，而且LCBP算子仅对图像的旋转和灰度变化具有不变性，对于图像的其他几何变换并不具有不变性，从而大大限制了其应用范围.

基于特征脸的主成分分析方法（Principal Components Analysis，PCA）又称为K-L变换，是目前主流也是最为成功的线性鉴别分析方法之一［7].用低维子空间来描述人脸特征，实现在最小均方意义下寻找最能代表原始人脸数据的投影［8].因此，为了有效提高光照和姿态变化影响的人脸识别率，笔者提出一种基于Contourlet变换和PCA的人脸识别算法.首先，运用Contourlet变换对人脸图像进行处理，得到包括眼、耳、口、鼻和姿态等人脸图像特征信息的低频子带，去除人脸图像中光照等高频噪声.然后，对人脸图像中的低频子带信息用PCA方法提取出人脸主要特征.最后，根据这些特征进行人脸识别.在著名的orl人脸数据库和Yale人脸数据库上的实验结果表明：基于Contourlet变换和PCA的人脸识别算法较好地保留低频子带图像中的人脸姿态信息，有效提升人脸识别率.

1 Contourlet变换

Contourlet变换［9]是一种多尺度、多方向的二维图像表示方法，相比于其他的多尺度几何分析方法，它具有多分辨率、局部定位、较强的多方向表示能力和各向异性等特点.Contourlet变换由拉普拉斯金字塔分解和方向滤波器组成，滤波器组如图1所示.首先由拉普拉斯金字塔变换对图像进行多尺度分解，得到原始人脸图像的低通采样和带通图像（原始图像和低通采样图像的差值图），即图像的低频子带和高频子带.然后，利用多方向滤波器（directional filter bank，DFB）将高频子带分解为2j个方向子带（j为滤波器参数）.对低频子带重复拉普拉斯金字塔分解即可实现图像的多尺度分解和多方向分解，有效避免图像低频信息的泄露.

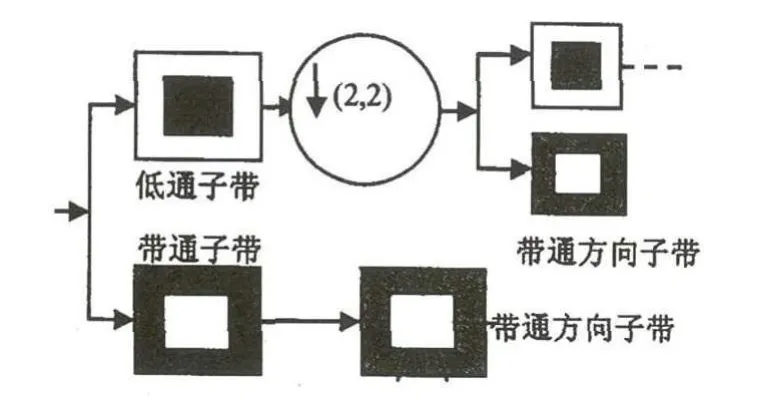
图1 Contourlet滤波器组图

2 PCA方法

PCA方法是由Turk和Pentland提出的一种基于特征点的人脸识别方法.主要思想是借助正交变换，将人脸相关的P个随机向量转化成分量不相关的K（K≤P）个随机向量，实现高维向量到低维向量的转换，形成低维线性特征子空间［10].通过低维表征向量，可以重构出所对应的原始人脸图像的高维向量.识别人脸过程中，将人脸图像投影到此低维特征子空间，用所得投影坐标系数与目标样本集中的投影系数进行比对，确定最佳特征脸.

为了更好地减少光照、姿态变化的影响，根据人脸图像直方图数据选择具有相似光照、姿态的n张人脸图像作为训练样本，每张人脸图像Ri表示成一个R（R＝M×N）维向量，则所有人脸图像数据可以用一个（M×N）×n维矩阵X来表示.

设xj表示第j幅人脸图像的向量，u为训练样本的平均向量，则

根据平均向量构造样本的协方差矩阵为：Sr…，xn-u]，则Sr＝AAT.

根据K-L变换，由协方差矩阵Sr的非零特征值组成新的人脸特征点坐标系，得到数据计算量非常大且冗余度较高.为此，引入奇异值分解定理（Singular Value Decomposition，SVD），通过计算V＝ATA来求得对应的特征向量，将这些人脸特征值按照从大到小的顺序排列，选取总能量大于指定值的特征值，求得的特征向量即为人脸主成分，构成的主成分矩阵即为“特征脸”空间.

最后，将训练样本中的每一幅人脸图像投影到“特征脸”空间，利用最小距离分类器比较分类，从而识别出此人脸图像是否是指定的人脸.

3 人脸识别过程及仿真实验

3.1 人脸识别过程

基于Contourlet变换和PCA的人脸识别算法的基本流程图如图2所示.

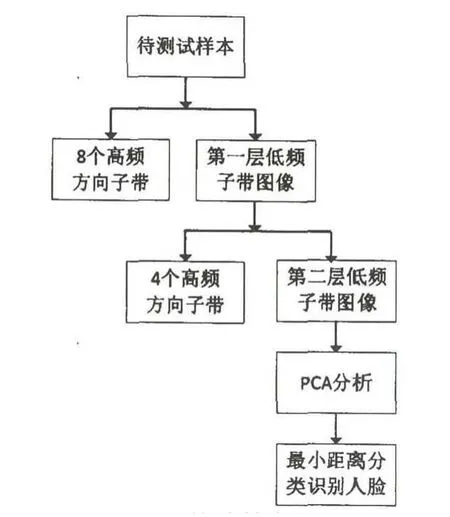
图2 算法基本流程图

1）对要测试人脸图像Ri（x，y）进行多尺度、多方向的Contourlet变换，分解得到图像的低频子带和高频方向子带，分解层数为2.其中，低频子带是图像的平滑逼近，包含人脸图像中所包含的眼、耳、口、鼻等大部分面部不变特征.高频方向子带包括了面部光照变化信息和图像的边缘和纹理信息.如果人脸图像尺寸为128×128，对图像进行2层Contourlet变换分解后得到的低频子带大小为32×32.通过2层Contourlet变换不仅捕获了人脸大部分信息，而且实现一定程度的降维效果，简化数据计算.

2）对变换后的低频子带进行PCA分析，提取更少维数的人脸特征信息.选择低频子带人脸图像前P个最大的特征值所对应的特征向量映射到特征脸空间，用所得投影坐标系数与目标样本集中的投影系数进行比较，确定最佳特征脸.通过PCA分析提取出维数更少的人脸特征进行识别.

3）由于上述方法对人脸图像数据进行处理时，造成数据之间的彼此独立，因此，将待测试样本所有子图像的距离求和，与原有特征向量进行融合，得到具有数据联系性的人脸特征向量，实现人脸识别.

3.2 仿真实验及分析

为了证明笔者算法与PCA算法在具有光照和姿态变化人脸识别过程中的优越性，实验选择在orl人脸数据库和Yale人脸数据库上进行.其中，orl人脸数据库中一共有40人，每人均有10幅人脸图像，部分图像包括了光照、姿态和表情的变化.Yale人脸数据库包括15个人的人脸图像，每张图像均有光照、表情的变化，但姿态视角不变.

3.2.1 在ORL人脸数据库上的实验

在ORL人脸数据库中选择每个人的前5幅图像作为训练样本，后5幅图像作为测试样本，则训练样本和测试样本均为200个.为降低计算复杂度和研究方便，对人脸图像进行Contourlet变换前，先将每幅人脸图像通过Matlab函数处理为128×128.

实验时，将待测试人脸图像分成i（i＝1，2）层，每层分解为2i个方向，得到的低频子带图像的大小分别为64×64和32×32.结果如图3所示.

图3 contourlet分解后的人脸图像

分解完成后，提取低频子带图像，按照前面所述第3.1项下第2）步骤与PCA结合.为了比较PCA人脸识别方法和基于Contourlet变换和PCA的人脸识别方法在不同能量阈值下的人脸识别率，调整能量阈值以5为步长，测试人脸识别率随能量百分比变化的实验，结果如图4所示.

数据显示：利用PCA方法继续对Contourlet变换后的低频子带图像进行人脸识别，与普通的PCA方法得到的人脸识别率相比大部分情况下有小幅提升，证明了Contourlet变换在人脸识别过程中的优势.

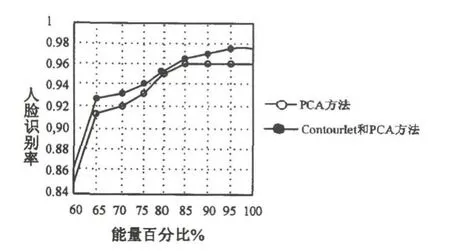
图4 识别率随能量变化图

3.2.2 在Yale人脸数据库上的实验

为了更好地验证Contourlet变换的低频子带图像对人脸识别率的影响，继续在Yale人脸数据库上采用上述方法进行测试.实验选择Yale人脸数据库中每个人的前5幅图像作为训练样本，后6幅图像作为测试样本，则训练样本总数为75个，测试样本为90个.不同人脸数据库中的低频子带图像的识别率如表1所示.

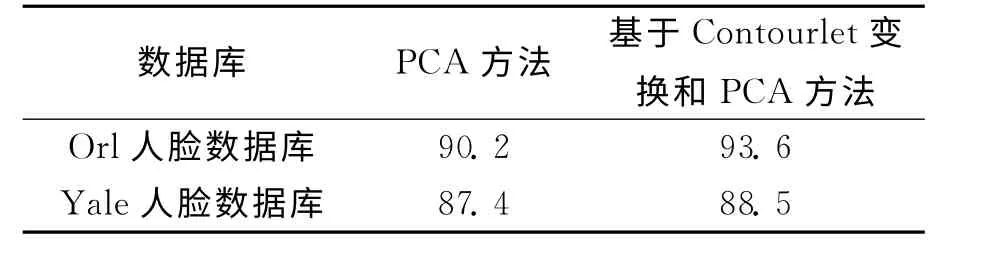
表1 不同人脸数据库中的人脸识别率／%

数据显示，笔者算法与PCA方法相比，无论是对于姿态变化明显、光照变化不明显的orl人脸数据库来说，还是对于光照变化明显、姿态变化不明显的Yale人脸数据库来说，均能有效提升人脸识别率，获得比较满意的人脸识别结果.但是，两个数据库的识别率相比较而言，orl人脸数据库中的人脸识别率高于Yale人脸数据库中的人脸识别率.其原因在于Contourlet变换的低频子带图像记录了人脸眼、耳、口、鼻和姿态的不变特性，对光照比较敏感.orl人脸数据库中人脸图像主要有姿态的变化，光照变换不明显，Yale人脸数据库中光照变化较明显.由此可见，Contourlet变换和PCA方法能够较大提升姿态变化的人脸识别率，但对光照变化的人脸识别率影响不明显.

4 结论

笔者针对传统PCA方法在人脸识别过程中光照、姿态影响下识别率降低的问题，结合多尺度几何分析提出了一种基于Contourlet变换和PCA的人脸识别算法，有效降低数据维度，过滤光照、姿态等高频噪声.对人脸图像进行主成分分析之前，先用Contourlet变换进行2层分解，得到包括眼、耳、口、鼻等大部分面部不变特征的低频子带图像和光照变化信息的高频子带图像.然后利用PCA分析选择低频子带人脸图像前P个最大的特征值所对应的特征向量映射到特征脸空间.最后将提取出的低频特征以及高频统计特征组合成特征向量进行人脸识别.通过在orl人脸数据库和Yale人脸数据库上进行仿真实验，数据证明基于Contourlet变换和PCA的人脸识别算法能够有效提升具有一定姿态变化的人脸图像，但对光照变化的人脸图像识别率提升不够明显.如何提取包含在高频子带图像中的光照和边缘信息，将其与低频子带分量进行融合是后续需要进一步研究的内容.

［1]秦宏伟，孙劲光，王强，等.基于自适应预处理和PCA的人脸识别方法的研究［J].计算机工程与应用，2011，47（14）：186-198.

［2]Jonathon P P，Todd S W，Alice J，et al.Face Recognition Vendor Test 2006：FRVT 2006Report Results［R／OL].［2014-04-06].http：／／www.frvt.org／／docs／FRVT，2006and ICE 2006Large Scale Report.pdf.

［3]WANG QingJun，ZHANG Rubo，PAN Haiwei.Face Recognition Based on Kernel Orthogonal Local Discriminant Embedding［J].Journal of Optoelectronics Laser，2010，21（9）：1386-1389.

［4]Li Yibo，Li Junjun.Harris corner detection algorithm based on improved contourlet transform［J].Procedia Engineering，2011（15）：2239-2243.

［5]Dong Yongsheng，Ma Jinwei.Feature extraction through contourlet subband clustering for texture classification［J].Neurocomputing，2013，116：157-164.

［6]Mosleh A，Zargari F，Azizi R.Texture Image Retrieval Using Contourlet Transform［C].International Symposium on Signal，Circuit and Systems，Laso，2009：1-4.

［7]Kwak K C，Pedrycz W.Face Recognition Using an Enhanced Independent Component Analysis Approach［J].IEEE Trans Neural Networks，2007，18（2）：530-541.

［8]Turk M，Pentland A.Eigenfaces for Recognition［J].Journal of Cognitive Neuroscience，1991，3（1）：71-86.

［9]Minh N D，Vetterli M.The Contourlet Transform：An Efficient Directional Multiresolution Image Representation［J].IEEE Transactions on Image Processing，2005，14（12）：2091-2106.

［10]周文刚，孙挺.基于分块颜色和形状的图像检索方法［J].周口师范学院学报，2008，25（5）：28-31.