一种快速的基于稀疏表示的人脸识别算法

龙法宁， 杨夏妮

（玉林师范学院计算机科学与工程学院，广西 玉林 537000）

一种快速的基于稀疏表示的人脸识别算法

龙法宁， 杨夏妮

（玉林师范学院计算机科学与工程学院，广西 玉林 537000）

基于稀疏表示的人脸识别算法(SRC)识别率相当高，但是当使用l1范数求最优的稀疏表示时，大大增加了算法的计算复杂度，矩阵随着维度的增加，计算时间呈几何级别上升，该文提出利用拉格朗日算法求解矩阵的逆的推导思路，用一种简化的伪逆求解方法来代替l1范数的计算，可将运算量较高的矩阵求逆运算转变为轻量级向量矩阵运算，基于AR人脸库的实验证明，维度高的时候识别率高达97%，同时，计算复杂度和开销比SRC算法大幅度降低95%。

稀疏编码；分类方法；人脸识别；小波变换；快速算法

模式识别领域，人脸识别的研究相当广泛，各种算法层出不穷。特别在近两三年对压缩感知技术研究浪潮下，Wright等[1]把稀疏表示和人脸识别算法结合起来，获得了相当高的识别率，基本方法是把所有人脸样本的集合看作训练集并构造为一个超完备字典，而测试的人脸样本则可通过该超完备字典进行稀疏表示。这个表示不但是稀疏的，而且仅包括所有训练样本的小部分，对应其他样本的稀疏解理想状态下应该都为零，对于这个超完备字典而言，它是测试样本最佳的稀疏表示。并且它可以通过l1范数最小化求得。因此寻找最佳的稀疏表示就能相对完美地区分出不同类别的训练样本，但是随之而来的就是计算机的运算时间大幅度增加。

基于稀疏表示的 SRC人脸识别算法[2]通过构造一个用作训练的超完备字典其中 Ai是第i类人脸数据的集合，由同类的n幅人脸图像形成训练字典，每幅图像有m个像素点作为矩阵 Ai的一列，n是训练数据的类别个数。假设b为第i类的一个测试样本，则b可由A线性表示为：

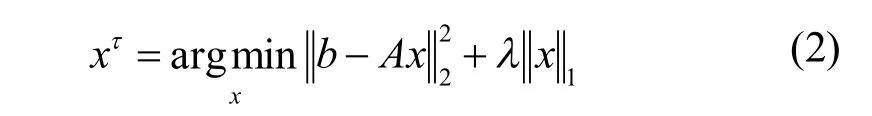
其中λ是一个很小的常数，那么对测试样本b的分类方法如下所示：

1 SRC算法时间开销分析

通过SRC算法的介绍和分析，发现除了对字典A的降维以外，时间开销主要集中在求解欠定方程组 y=Ax的最优稀疏解。通常情况下，欠定线性方程是没有唯一解的，由于最优重构信号的求解计算复杂度很高，所以大多数研究聚焦在寻找可接受复杂度下的近似解（次优解）。求次优解是把l0范数放宽到l1范数通过线性规划求解的，但是l1范数求解的计算复杂度仍然很高。经证明可知道l2范数是用来度量重构误差的，需通过l2范数最小化问题找近似解，用l2范数代替l0范数，虽然有一定的误差，但是可以解决l0范数可能无解的问题，同时在识别率有小幅下降的情况下，计算时间有很大的下降。现在的算法是求得的解更加精确，但是计算复杂度更高，为了克服这一缺点越来越多的快速l1-min算法被提出。例如同伦算法、迭代收缩阈值、近端梯度、增广拉格朗日乘子和梯度投影算法等[3]。

快速l1-min算法各有优点，在运算速度和正确率两方面，无论是那一种算法在任何条件下都不可能达到最好。实际的应用当中，必须充分考虑人脸数据的特点以及应用环境，在运算速度和正确率之间找到平衡点，以达到最好地使用效果。因此在对识别响应速度比较高的情况下，即使损失很小的识别率，也需要解决求解l1-min时间代价过大的问题。

2 基于Gabor小波的表情特征提取

文献[4]通过分析Gabor小波和稀疏表示的生物学背景和数学特性，提出一种基于Gabor小波和稀疏表示的人脸表情识别方法。采用Gabor小波变换对表情图像进行特征提取，建立训练样本Gabor特征的超完备字典，通过稀疏表示模型优化人脸表情图像的特征向量，利用融合识别方法进行多分类器融合识别分类。但是该方法的综合识别率只有82.3%，并不是很理想。文献[5]提出了一种结合Gabor小波特征和SRC算法的人脸识别方法，AR人脸库的识别率在图像降维到300维的时候是95%比SRC的87%提高了8%，而维度超过500维时，最高识别率达到了97.14%，依然比SRC的91.19%提高了6%，但是对Gabor特征降维后图像数字字典的时间开销O(n2)是通过列向量从8781降到917维，维数依然很高，同时求解欠定线性方程采用的方法和SRC算法一致，运算量一致。

因此，本文依旧采用Gabor小波变换来提取表情图像的初始特征，然后采用别的方法来降低求解线性方程组的计算时间，文献[6]给出了第j个二维Gabor小波滤波器的公式定义：

式(4)中，σ是与小波频率带宽有关的常数，z= (x ,y)为空间位置坐标，κ确定了Gabor内核的方向和尺度。例如，在采用8个方向和5个尺度的采样时，某人方向和尺度上的κ可以写为其中为采样尺度，为尺度标号；为采样方向，为方向标号。Kmax为最大频率，f是频域中的内核间隔因子。令参数可以获得较好的小波表征和辨别效果。

对人脸图像进行Gabor小波变换，就是将人脸图像和Gabor小波的核函数进行卷积。人脸表情图像像素点z=(x, y)处的Gabor小波特征值是通过式(4)的滤波器与图像的灰度值ψ ( κ ,z)卷积计算得到：

设 Jk(z)的幅值和相位分别为 Ak和 φkφk，则组合不同尺度和方向的 J(z)，构成

k图像在z位置处的Gabor特征矢量，因此每幅人脸图像可以通过式(4)获得小波处理后的新图像，构为新的训练字典。

由于Gabor特征具有良好的空间局部性和方向选择性，而且对光照、姿态具有一定的鲁棒性，因此在人脸识别中获得了成功地应用。设图像的大小为m×n，通过40个滤波器得到Gabor特征的维数高达40×m×n，计算量很大，且由于Gabor特征在相邻像素间是高度相关和冗余的，所以通常只需要稀疏的提取部分节点上的Gabor特征，因此可以把Gabor的特征提取和SRC算法结合起来。

3 快速稀疏分类算法

一般来说人脸数据都是可以使用稀疏的信号来表示。那么如果给定测试人脸b是稀疏的或者是可压缩的，可以通过解如下形式的优化问题而获得稀疏解：

由于SRC算法要获得良好的人脸识别率，希望求得的解是尽可能的稀疏，而求解l1范数的常用方法有贪婪算法、凸优化算法等，无一例外，都是通过不断的迭代计算来获得最优的稀疏解，花费的时间代价相当大。

既然测试人脸b可由A线性表示为 b= Ax，则如果求得 A-1则公式可以转换为： x = A-1b ，令于是有：

由于 xTATb是一个数，而这个数的转置是它的本身，因此有：

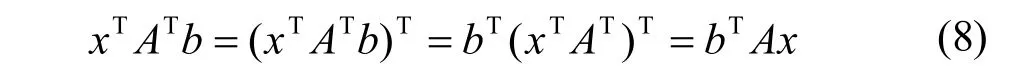
故式(7)可化为：

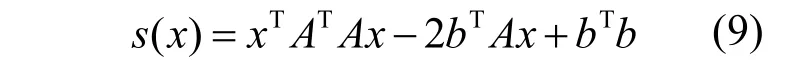
由式(9)得：

若x*是 s( x)的极小点，则必有 ▽ s( x )=0，则：ATAx = ATb 即 x =(ATA)-1ATb。

上述方程组的解法需要 ATA正定才能求得ATA的逆，实际问题并不能保证 ATA正定，因此遇到这种情况，修正方法是现在矩阵A对角线k

上的元素都加上同一个数 μ ＞0，则上述方程变为：

这样做的目的是：即使 ATA是奇异的，μ是一个很小的数，但是只要将μ取得充分大，总能使(ATA+ μI)正定，从而 (ATA+μI )x=ATb 肯定是有解的。因此，式(11)的目的是通过最小化误差的平方和寻找数据的最佳函数匹配。从而可以简便地求得未知的数据，并使得所求数据与实际数据之间误差的平方和最小，从而可以粗略模拟l2范数的计算。

综合上述讨论，快速稀疏分类的算法描述的具体步骤如下：

假设在给定的训练集 B =[B1,B2,…,Bn]中有k类已经标记好的样本，其中第i类中含有ni个样本。每个人脸样本对应于矩阵中的一个列向量 Bi, m为人脸图像的维数。

Step 1. 对人脸库构造训练样本集B，然后对B进行小波变换得到新的字典 A= Gabor(B)，同理对测试集也进行小波变换。

Step 2.对训练样本集A中的每一个列向量进行PCA降维，同理也对测试集进行PCA降维，以确保矩阵是正定的，并且每张人脸的维数需要比人脸的个数要小，即构成欠定矩阵。

Step 3.对训练集和测试集的每一个列向量 b利用式(11)进行不太精确的稀疏编码，得到稀疏表示其中求逆 A-1并不采用求解l1范数的最小化算法，而采用向量矩阵的轻量级运算其中I是单位矩阵，μ是一个很小的值， (ATA+ μI )-1可以通过求解矩阵伪逆获得。

Step 4.对稀疏表示后的训练集和测试集采用SVM或SRC分类器进行分类决策。

4 实验结果及分析

4.1 AR人脸库识别率

在实验中，采用AR人脸数据库[7]，从数据库中选出50个男性对象和50个女性对象组成数据库子集。其中，每个对象选择 14幅仅有光照、表情变化的图像，其中来自第一时间拍摄的7幅人脸图像作为训练集，另外的7幅人脸图像作为测试集，那么，训练集和测试集各有700幅人脸图像，一共是1400幅人脸图像，如图1所示。

图1 AR无遮挡人脸库

对 Gabor核函数中相关参数的取值为v=5,u =8，对一幅人脸图像进行5个尺度8个方向上的Gabor小波变换。SVM分类器采用LIBSVM工具包的多类别SVM分类器，分类函数的参数是(′-s 1 -t 3 -c 1.2 -g 1.2′)，分别对测试集和训练集的 1400幅图片进行小波变换以后通过PCA分别降维为54、120、300维后进行训练学习和测试，实验结果如表1所示，本文的方法(简称Gabor+FastSparse+SVM)。本文方法的识别率在维度超过300以后，就接近甚至超过了结合小波变换的SRC算法。从表2可以看到，当维度到达500的时候，识别率最高可以达到97.14%以上，和文献[5]所采用Gabor+SRC的最佳识别率基本一致，因此可以看到本文方法拥有相当高的识别率。

表1 各种人脸识别算法对比(%)

表2 快速稀疏识别算法高维识别率和计算时间

4.2 算法时间开销

在CPU为Intel Core2 Duo E 7300 ，频率为2.66 GHz，内存为4 G的台式机电脑上，对以上算法进行了时间统计，为了获得高识别率，不管是SRC算法还是本文的方法，都需要对人脸库进行小波变换，其所花费的时间需96.818965 s，因此下面只对排除小波变换所需的运算时间以外的识别时间进行统计对比，其中SRC算法采用L1_magic工具包求解稀疏信号重构的凸优化方法[8]。实验结果如表3所示，本文的方法所耗费的时间比SRC的算法减少了95%以上。

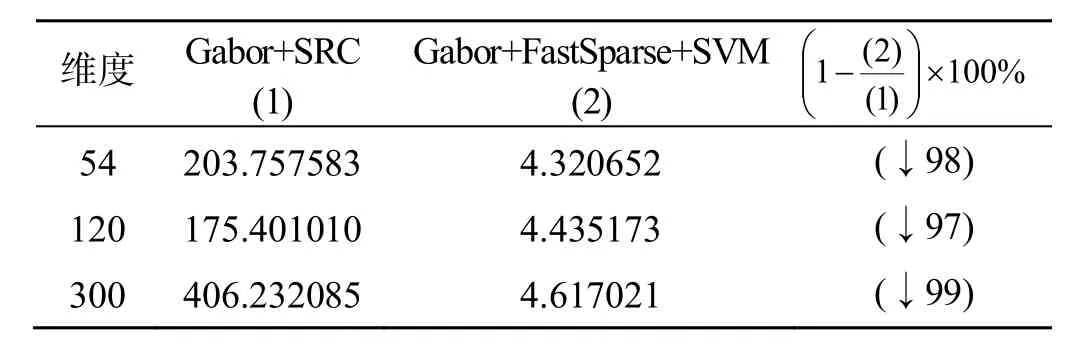
表3 运算时间对比(s)

5 结 束 语

本文方法在保留小波变换特征提取的 SRC算法的高识别率的基础上，大幅度地降低了识别时间。其原因是基于稀疏表示的SRC算法，为了保留高识别率，必须求解l1范数的最小最优解，使稀疏解尽可能的最小化，因此迭代时间过长，而本文采用了轻量级固定公式运算来代替求解l1范数，从而减少了大量的时间，在稀疏解不够稀疏的情况下，选择了采用 SVM分类方法而不是 SRC的分类方法，从而保留了较高的识别率，实验证明，在没有优化SVM的核函数的基础上，当图像降维后大于500维的时候，最大达到了97%的识别率，如果排除小波转换训练字典和测试字典的时间，识别分类所减少的运算时间达到95%以上，因此有较强的实用价值，下一步工作，如果采用类似图片分块的识别方法，相信还可以获得更佳的识别率。

[1] Wright J, Ma Yi, Mairal J, Sapiro G, Huang T, Yan Shuicheng. Sparse representation for computer vision and pattern recognition [J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044.

[2] Wright J, Yang A Y, Ganesh A, Sastry S S, Ma Y. Robust face recognition via sparse representation [J]. IEEE PAMI, 2009, 31(2): 210-227.

[3] 刘 杰, 李昆仑. 快速 L1范数最小化算法的性能分析和比较[J]. 电脑知识与技术, 2011, 7(19): 4641-4643.

[4] 张 娟, 詹永照, 毛启容, 邹 翔. 基于 Gabor小波和稀疏表示的人脸表情识别[J]. 计算机工程, 2012, 38(6): 207-208.

[5] Yang Meng, Zhang Lei. Gabor feature based sparse representation for face recognition with Gabor occlusion dictionary [J]. Proc. European Conf. Computer Vision, 2010, 6(5-11): 448-461.

[6] Liu Chengjun, Wechsler H. Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition [J]. IEEE IP, 2002, 11(4): 467-476.

[7] Martinez A, Benavente R. The AR face database [R]. CVC Tech. Report, 24. 1998.

[8] Kim S J, Koh K, Lustig M, Boyd S, Gorinevsky D. A interior-point method for large-scale l1-regularized least squares [J]. IEEE Journal on Selected Topics in Signal Processing, 2007, 1(4): 606-617.

A Fast Face Recognition Algorithm Based on Sparse Representation

Long Faning, Yang Xiani
(Computer Science Department, Yulin Normal University, Yulin Guangxi 537000, China)

As a recently proposed technique, sparse representation based classification (SRC) has been widely used for face recognition (FR). Sparse representation based SRC algorithm has a high recognition rate. While l1-minimization (l1-min) has recently been studied extensively in optimization, the high computational cost associated with the traditional algorithms has largely hindered their application to high-dimensional, large-scale problems. This paper devotes to analyze the working mechanism of SRC and discusses accelerated l1-min techniques using augmented Lagrangian methods, consequently, we propose a very simple yet much more efficient face classification scheme. The performance of the new algorithms is demonstrated in a robust face recognition of AR database. The experimental results verify that these methods can greatly improve the face recognition speed rate (97% decrease), and maintain a high recognition rate (95%). These methods are of practical values.

sparse representation; classification method; face recognition algorithm; gabor wavelet; fast algorithm

TP 311

A

2095-302X(2014)06-0889-04

2014-05-29；定稿日期：2014-07-16

广西教育厅科研立项项目桂教科研〔2011〕14号文件资助项目(201106LX512)；玉林师范学院青年科研资助项目(2010YJQN19)

龙法宁(1978-)，男，广西玉林人，讲师，硕士研究生。主要研究方向为图像处理、模式识别。E-mail：longfaning@163.com