基于几何法立体图像校正的研究

王道累， 杨 峰

（上海电力学院能源与机械工程学院，上海 200090）

基于几何法立体图像校正的研究

王道累， 杨 峰

（上海电力学院能源与机械工程学院，上海 200090）

立体视觉图像校正是加速立体匹配简单而常用的技术之一。采用几何法对使用棱镜的单镜头立体视觉系统图像进行校正，根据成像原理，从图像平面像素点反推到三维实体点的分析运算，利用成像光线几何关系求解虚拟相机外部参数，实现极线的校正，避免了复杂相机标定过程。同时，该算法可以从双棱镜应用推广到多面棱镜的单棱镜立体视觉系统图像校正。实验结果表明，基于几何法对使用棱镜的单镜头立体视觉系统图像校正是有效的。

立体视图；极线校正；图像处理；几何法

立体视觉图像校正是计算机视觉技术的关键技术之一。图像校正的目的是使两幅非共面图像校正成两幅共面。同时确保两幅图像相对应极线成为共线并沿着水平扫描线。因此，通过立体图像对的极线校正，使立体匹配算法的搜索范围从二维的图像平面降低到一维的扫描线上，从而大大提高匹配算法的搜索速度和精度[1-3]。

视图校正是立体视觉的一个典型问题。Al-Shalfan等[4]最早提出基于光学技术的校正方法，该方法主要是通过硬件技术来实现的，因而在实践应用中受到了很大地限制。而Loop和Zhang[5]提出了对立体视图校正方法分解单应性矩阵。Isgro和Trucco[6]提出了一种不需要对极线几何求解，尤其是基础矩阵进行精确计算的图像校正方法，直接利用了校正后的基础矩阵有一个特定的已知形式来建立水平视差最小化式子，从图像的对应点直接产生校正的单应性矩阵。Hartley[7]提出了一种针对视角变化比较大的立体图像对进行校正的方法。Yu和Wu[8]提出了一种减少校正后图像几何畸变的方法，把校正问题和基础矩阵的估算问题结合起来，从基础矩阵的估算中求得校正问题的最小二乘解，通过增加剪切变换使单应性矩阵唯一，减少整幅图像的几何畸变。该方法在优化过程中，优解的获得可能陷入局部最小化。综上所述的视图校正算法多存在一定的局限性。因此，设计一种简单而实用的立体图像校正算法是立体视觉的重要研究方向之一。

基于棱镜的单镜头立体视觉系统是本论文研究的对象，该系统利用棱镜来形成多个虚拟相机。这与传统立体视觉系统利用两个或多个相机捕获两幅或多幅从不同视角的场景相同。但是该系统简单而有效地减少了相机标定参数复杂计算过程。另外，图像的采集也不存在时间差，同时也节省系统设备建设的费用。

本文运用成像原理，从图像像素点反推到三维实体点，建议使用几何分析方法求解虚拟相机的外部参数等。本文优势及特点有：①几何分析方法求解虚拟相机参数，减少了复杂的相机标定过程；②使用基于棱镜的单镜头立体视觉系统，直接利用棱镜来形成虚拟相机，减少了相机布局误差；③几何分析算法可以进行总结并一般化。

1 相机模型定义及立体图像校正

1.1 相机模型定义

针孔相机模型是由光心O和图像平面建立而成的。一个三维空间点P到图像平面投影点p是直线OP和图像平面的交点。含O和图像平面正交的线被称为光轴，它与图像平面的交点为(ox, oy)。摄像机光心O到图像平面的距离，即摄像机的焦距f。

假设在世界坐标系下坐标P=[X, Y, Z]T和在图像平面（像素）坐标p=[u, v]T。从三维映射坐标二维坐标的透视投影，这是由一个线性齐次坐标变换表示。和分别为P和p的齐次坐标；然后，由P到p投影变换关系得：

其中s是一个比例因子，ppmP 是相机的投影矩阵。分解投影矩阵：

矩阵intM 是相机内部参数形成的矩阵，具体表示：

f是焦距，sx和sy分别是像素在水平和垂直方向上的有效尺寸(mm)。摄像机的位置和方向（外部参数），是由3×3旋转矩阵R和平移矢量T组成。图1所示为立体视图极线几何关系（实线）。

图1 立体视图极线几何(实线)和校正后的极线几何(虚线)

2 单镜头的双目立体视图校正

2.1 单镜双目头立体视觉系统

本文以单镜头立体视觉系统为研究对象，该系统使用棱镜来形成两个或多个虚拟相机。图 2所示是使用双棱镜的单镜头立体视觉系统。系统设计规则如下：

(1) 将双棱镜放置于相机的前面，由棱镜顶点与相机镜头在一条直线上；

(2) 棱镜后平面与相机的图像平面平行；

(3) 图像的中心点与棱镜顶点的直线为Z轴，并将双棱镜分为上下对称。

通过设置好双棱镜和相机位置，根据成像原理，真实相机发出光线通过棱镜反射及折射作用，可以形成两个虚拟相机（如图2所示）。当采集图像时，就可以得到两幅不同视角的图像。这种单镜头立体视觉系统使用棱镜来形成多个虚拟系统有几个优点：①相机标定变得简单；②在建设系统所需的费用减少；③对所产生的误差相对的减小；④虚拟相机的焦距与真实图像的焦距一样；⑤可以同时获得多个视图，不存在时间差，对于运动的场景也可以瞬间得到一组视图。

1.2 立体图像校正

图 1显示了两视图的极线几何关系。如果两个相机已经被标定过，即两个摄像机投影矩阵是已知的。两个相机中心连线成为基线。然后，对所有视图通过校正矩阵变换计算后获得校正图像。校正后的图像极线共线且平行于基准（图 1虚线表示部分）。这样对搜索视图间匹配点变得简单有效。对于立体图像的校正，Yu和 Wu等[8]可知校正矩阵主要由内部参数矩阵和相机的姿态矩阵组成。而对于本论文研究课题内部参数矩阵，由系统设备提供。然而，外部参数将由本文提出的几何法来解决。

在上节中也讨论过了，立体图像的校正需要相机的内外部参数。这就需要对相机进行标定。而如果直接对相机进行标定，整个过程相当的复杂。所以本文利用图像成像原理进行几何法求解相机的外部参数包括旋转矩阵 R和平移向量 T。至于内部参数 Mint可以直接从相机获得固有参数。

图2 使用双棱镜的单镜头立体视觉系统

2.2 几何方法分析求解校正矩阵

已知 P (x ,y,- f)点坐标，光心 O(0,0,0)及焦距f，折射率n。棱镜顶点到真实相机光心的距离T0，双棱镜大小和角度α等。例如直线PM方程为：

接着，根据双棱镜布局位置，在世界坐标系下求得棱镜左平面方程：

其中， (X0,Y0,Z0)为棱镜顶点的坐标，为平面的法向向量。根据已知参数值和棱镜的几何位置即可求得法向向量。

直线MN可以通过向量的平行四边形法则，求得MN的方向向量（如图4）。然后，点 M (xM,yM,zM)的坐标可以从直线PM与双棱镜左平面求得：

图3 双目视觉的系统视图校正

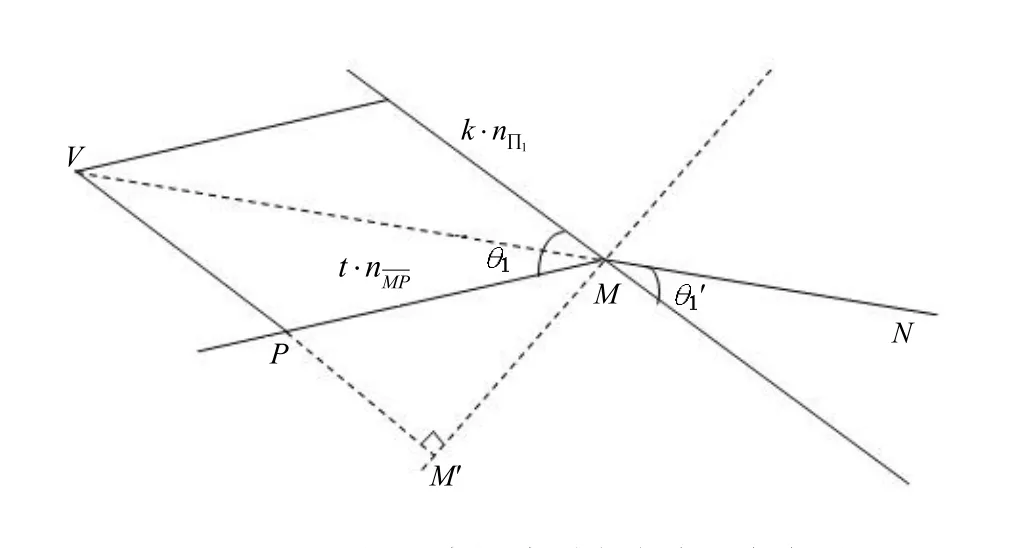
图4 运用平行四边行法则求直线方向向量

同理可得直线NS的方程。

以此类推，Z轴直线重复上述的步骤可求得经过双棱镜后直线 L方程。因此，虚拟左相机光心由两直线相交，求交点。

从图 4知，从真实图像平面到左虚拟图像平面的平移向量：

通过几何关系分析可得，旋转角度β等于直线L与Z轴的夹角。已知两方程就可得角度β。因此，旋转矩阵为

2.2.2 视图校正矩阵

定义虚拟相机新坐标系姿态矩阵：

其中， r1作为虚拟相机坐标系的 X轴，选择平行于基准线：r2作为虚拟相机坐标系的Y轴和真实图像系统的坐标系Y轴一致；r3作为虚拟相机坐标系的Z轴，右r1和r2叉积得到。

最后，两个虚拟图像平面的校正变换矩阵：

通过上面的步骤可以获得最终的校正后的图像坐标[2]。

3 单镜头的多目立体视图校正

建立单镜头的多目立体视觉系统可选用多面的棱镜。如图 5所示是利用三棱镜的单镜头视觉系统图。多目立体图像校正算法可由双目立体图像校正推理得到。同样进行几何成像反推求得旋转矩阵R和平移矩阵T。

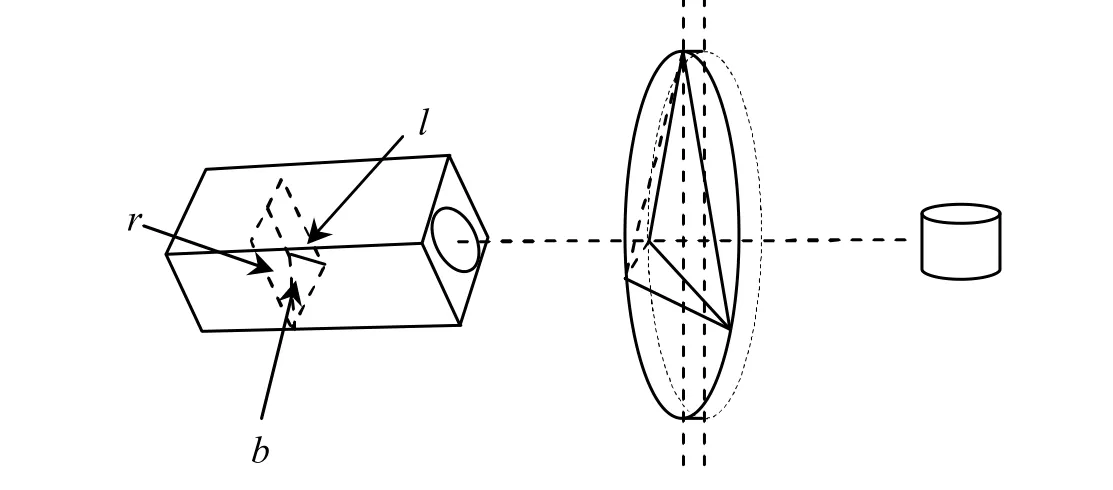
图5 三棱镜的单棱镜立体视觉系统

通过几何法分析，在三棱镜的单镜头视觉系统中，从虚拟图像平面到校正后的虚拟图像平面旋转角度β及γ（图6所示），即旋转矩阵：

最后，根据旋转矩阵R和平移向量T及新坐标系统姿态矩阵求取校正后的3个虚拟图像平面的校正变换矩阵，然后获得校正后的图像平面坐标。

图6 虚拟平面旋转图

同样思路推广与应用到四棱镜、五棱镜的单镜头视觉系统中（如图7～8所示）。

图7 四棱镜的单棱镜立体视觉系统

图8 五棱镜的单棱镜立体视觉系统

利用棱镜的单镜头视觉系统图像校正算法归纳与总结：

(1) 通过几何分析，运用平行四边形法则计算虚拟图像平面的旋转矩阵R和平移向量T，例如：

这里d=0或者1（针对多面棱镜）；

(2) 建立虚拟相机坐标的系统，构建新坐标姿态矩阵rectR ，定义各个坐标轴；

(3) 通过内部参数矩阵计算校正后的虚拟相机的图像坐标。

4 实验结果及讨论

本实验利用棱镜的单镜头视觉系统来采集图像。三幅图像分别来自双棱镜、三棱镜和四棱镜视觉系统采集。它们分别命名为“mechanical stand”、“red rose”和“da”。每幅图像都有两、三和四幅相同背景的图像从不同视角采集得到。这种采集手段相当于多个真实的相机从不同角度对一场景的拍摄。如图9(a)在左视图任意选取3个点，同时计算并画出其相对应右视图的极线，图 9(b)通过几何方法校正过后的左视图的 3个点及相对应右视图的极线。图 10(b)在上左视图任意选取 3个点，同时计算并画出其相对应下视图的极线图10(c)，图10(d)在上右视图取得3个点是和上左视图上是一致的，也画出其相对应下视图的极线图10(c)，图10(e)～(g)通过几何方法校正过后的上左视图、上右视图的 3个点及相对应下视图的极线。图11(a)上左视图任意选取3个点，同时计算并画出其相对应上右视图、下左视图和下右视图的极线如图 11(b)～(d)。经过校正过，各视图上的点极线都发生了变化，如图 12(a)～(d)所示。以上各视图从经过建议算法校正后的视图中的极线变成水平状态了。这样证明了本算法是有效的。

对三棱镜立体视觉系统进行匹配点测试。在图10中取8组左右视图像素点坐标，求取在第三幅视图中的匹配点。第三、四列坐标值为左右视图像素点在第三幅视图对应极线的交点坐标。表1显示使用传统的校正方法(张氏法)[9]和几何法的匹配求匹配点结果。从表 1中得到第三与第四列误差值的值一直小于第五与第四列误差值。匹配点由几何法和传统标定方法得到误差的平均距离分别为6.017和11.402。由此表明几何方法校正比传统的校正方法好。这种改善是由于几何分析方法比传统的校正方法可以得到更精确的虚拟摄像机外部参数。此外，结果验证本文的校正算法确实是有效，即使应用于单棱镜的多视图立体视觉系统。

图9 利用双棱镜视觉系统采集图“mechanical stand”

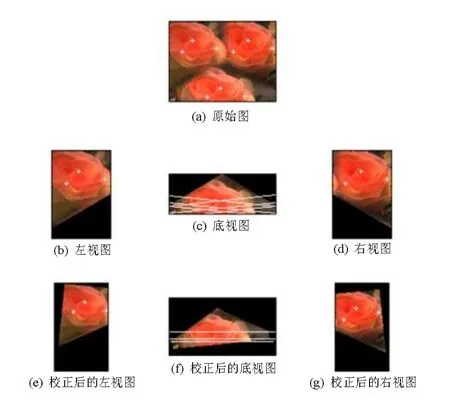
图10 利用三棱镜视觉系统采集图“red rose”

图11 利用四棱镜视觉系统采集图“达”

图12 利用四棱镜视觉系统校正图“达”

表1 张氏法和几何法的求匹配点结果

5 结 论

立体图像校正是计算机视觉中关键技术之一。通过对视图进行校正后，对寻找匹配变的更简单而且更加有效。本文根据成像原理，采用简单而且有效的几何分析方法解决立体图像校正变换矩阵。运用了平行四边形法则及成像的反推技术解出了旋转矩阵和平移向量。通过双棱镜的分析并推广到多面棱镜的单镜头立体视觉系统中，并且归纳总结视图校正算法一般步骤。实验结果显示，本文的建议算法是有效的。在未来的研究中，将完善这一方法，并应用到微型化的单镜头立体视觉系统中去。

[1] Fusiello A, Trucco E, Verri R. A compact algorithm for rectification of stereo pairs [J]. Machine Vision and Applications, 2000, 12: 16-22.

[2] Trucco E, Verri A. Introductory techniques for 3-D computer vision [M]. Prentice Hall, 2006: 156-245.

[3] Chen Zezhi, Wu Chengke, Tsui H T. A new image rectification algorithm [J]. Pattern Recognition Letters, 2003, 24: 251-260.

[4] Al-Shalfan K A, Haigh J G, Ipson S S. Direct algorithm for rectifying pairs of uncalibrated images [J]. Electronics Letters, 2000, 36(5): 419-420.

[5] Loop C, Zhang Zhengyou. Computing rectifying homographies for stereo vision [C]//IEEE Conference on Computer Vision and Patter Recognition, Fort Collins, CO, 1999: 125-131.

[6] Isgro F, Trucco E. Projective rectification without epipolar geometry [C]//IEEE CVPR, 1999: 1094-1099.

[7] Hartley R. Theory and practice of projective rectification [J]. International Journal of Computer Vision, 1999, 35(2): 115-127.

[8] Yu Yuhua, Wu H H, Projective rectification with reduced geometric distortion for stereo vision and stereoscopic video [J]. Journal of Intelligent and Robotic Systems, 2005, 42(1): 71-94.

[9] Zhang Zhengyou. A flexible new technique for camera calibration [C]//IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

Research of Stereo Image Rectification Based on a Geometrical Approach

Wang Daolei, Yang Feng
(College of Energy and Mechanical Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

This paper proposes a geometric approach for rectification on uncalibrated single-lens stereovision using a prism. According to the imaging principle, the points of 3D entity can be estimated from the image plane pixels. In order to rectify epipolar lines, the optical geometry of imaging is utilized to solve virtual camera extrinsic parameters, which avoids the complex camera calibration process. At the same time, the algorithm can be applied torectify images based on single-lens stereovision system using a bi-prism to polyhedral prism. Experimental results are presented to show the effectiveness of the approach.

stereovision; polar correction; image processing; geometrical approach

TP 391

A

2095-302X(2014)06-0883-06

2014-04-17；定稿日期：2014-05-25

王道累(1981-)，男，上海人，讲师，博士。主要研究方向为计算机视觉、图像处理、CAD/CAM。E-mail：alfredwdl@shiep.edu.cn