基于扫描区间表示的不规则多边形快速定位算法及应用

罗月童， 吕 师， 江玉清

（合肥工业大学计算机与信息学院VCC研究室，安徽 合肥 230009）

基于扫描区间表示的不规则多边形快速定位算法及应用

罗月童， 吕 师， 江玉清

（合肥工业大学计算机与信息学院VCC研究室，安徽 合肥 230009）

不规则多边形定位算法是排料算法的重要组成部分，其效率对排料算法的性能有重要影响。基于扫描区间表示的不规则多边形定位算法因能适应任意复杂多边形而被广泛采用，但它存在计算量大的不足。通过深入研究基于扫描区间表示的多边形定位算法，该文从两个方面对其方法进行改进：首先提出候选平移位置矩阵的概念，进而实现定位扫描算法；然后通过最大跨度比较法快速排除一些不可能的行，从而通过减少定位扫描算法的调用次数进一步加速。该算法已应用于自主开发服装排料软件，多个实际衣片数据的测试结果证明了该文算法的有效性和高效性。

排料；扫描区间表示法；不规则多边形；定位算法

排料问题广泛应用于金属板材、木料、玻璃、布料等下料问题，设计重工业、轻工业、微电子等不同领域。人们也对相关问题进行了广泛研究[1]。

排料问题实质上是一个二维不规则图形排样问题，是一个非确定多项式(non-deterministic polynomial, NP)问题。基于左下优先排样算法(bottom-left, BL)[2]和可填充式左下优先排样算法(bottom-left-fill, BLF)等启发式策略，排料问题可分成两个步骤：一是确定多边形序列的摆放顺序和角度；二是根据顺序进行摆放二维图形。

确定二维图形的摆放顺序和角度是一个组合爆炸问题，人们使用多种优化算法[3]进行近似求解，如神经网络[4]、遗传算法[5]、模拟退火[6]、粒子群优化算法[7]。本文选用遗传算法选择二维图形的摆放顺序和角度。因为每改变一次二维形状的摆放顺序都要重新进行摆放，因此，二维形状定位算法的效率对排料算法有重要影响。常用方法有矩形包络法[8-9]、NFP算法[10-11]、基于扫描区域的算法[12]等。其中，基于扫描区域的二维形状定位算法因能处理复杂形状而备受关注，但它存在时间效率低下的缺陷。本文通过深入分析基于扫描区间的二维形状定位法，从两个方面改进该算法，实现快速基于区域扫描的二维形状定位算法。

1 基于扫描区间的任意多边形定位算法

文献[12]详细地介绍了这个方法，本文简要描述该方法。

1.1 过程描述

扫描区间定位算法依据图形学中多边形扫描转换的思想，将待排多边形和原料多边形表示为一系列扫描区间，从而将复杂的任意多边形判交过程，转换为简单的扫描区间判交过程。扫描区间表示法的每个扫描区间由一对x坐标值构成，而原料多边形的扫描区间中另外加入了脏位标志DF(1表示已占用，0表示空闲)。通过比较待排件和原料多边形上扫描区间表示的x坐标值，结合DF的值，判断右移距离。假设要判断原料多边形上某位置positon处是否可以放下排样件，若发现待排件中扫描区间[px1, px2]和板料上的扫描区间[sx1, sx2]有重叠部分，且DF=1，那么位置 positon处不能放下排样件。排样件直接右移距离offset=[sx2-px1]，接着判断下一位置定位情况。假设原材料多边形上已经放置了一系列多边形，此时需要确定一个待排多边形的可行位置，待排多边形的移动过程如图1所示。

图1 待排件多边形排放过程

扫描区间定位算法对待排件序列进行以下操作：

(1) 初始位置 position(x, y)设置为原料矩形左下角。

(2) 依次取排样件Polygon(a)。调用“定位扫描算法”，Polygon(a)是否可以放在位置 position(x，y)处。如果可以，把排样件Polygon(a)排放position(x, y)处；返回第(1)步，排放下一个待排件。

(3) 依据“定位扫描算法”计算得到Polygon(a)右移的距离 offset, x=x+offset，即 position(x,y)= position(x, y)+offset。

如果在x方向上排样件Polygon(a)超出原料矩形范围，y=y+1, x=0；

如果在y方向上排样件Polygon(a)超出原料矩形范围，待排多边形Polygon(a)在原料上排放不下。

返回到第(2)步。

其中第(3)步调用了“定位扫描算法”，用来判断位置 position(x, y)处是否可以放置待排件对象，算法简单描述如下：

(1) 初始扫描的位置position(x, y), i=0。

(2) 对Polygon(a)取第i条扫描线与之相交的所有扫描区间；对原料矩形取第(y+i)条扫描线与之相交的所有扫描区间。

(3) 对从步骤(2)得到的 Polygon(a)上的每一个扫描区间[px1, px2]，增加位移x之后得到区间[px1+x, px2+x]；对从步骤(3)得到的原料矩形的每一个扫描区间[sx1, sx2]，如果扫描区间[sx1, sx2]的脏位DF=1，且与[px1+x, px2+x]发生重叠，那么计算 Polygon(a)可以直接右移的距离值 offset=sx2-(px1+x)，同时返回FALSE，退出定位扫描算法。

(4) i=i+1，如果i大于经过Polygon(a)的扫描线条数，返回 TRUE，表示 Polygon(a)可以定位在位置position(x, y)处。

返回到步骤(2)。

1.2 问题分析

为保证紧凑的排放效果，多边形从初始位置出发，即其包围盒左下顶点位于原点的位置开始，寻找可行的排放位置。假设原材料多边形中已排放若干多边形，现在要对新入的多边形进行排放，如图2(a)所示。

图2 文献[12]方法问题分析

(1) 缺少完善的移动策略。当确定了待排件在y方向上某个位置后，横向定位的过程实质上就是多次调用定位算法，获得新的offset值，并且不断地验证，最终找到可排放位置的过程，但过程中不可避免地出现反复定位。

例如，经过若干次扫描区间定位算法，过程中会得到图2(b)所示虚线位置。由于新位置只能保证多边形部分扫描区间与原料扫描区间无重叠，因而该位置并不一定是最终可行位置，再次调用扫描区间定位算法，从下到上比较待排多边形每行扫描区间，发现多边形对应位置扫描区间与原料中扫描区间（A，B）重叠，通过计算获得新的offset值，如图2(c)所示，并且再次使用定位扫描算法，判断新位置的定位情况。如此反复必然会造成时间复杂度的提高。

最坏的情况是经过一系列的比较后判定该y值下没有可选位置排放待排多边形，那么此y值下复杂的比较过程实质上是不必要的。如图2(d)所示，待排多边形多次比较后移动到图形2所在位置，发现超出原料边界，因而返回最左位置，并且y方向上移动到图形3所在位置，重新计算新的offset。特别是当待排多边形复杂度较高，扫描区间数的增多，重复且不必要的比较过程会越来越多，严重降低算法的时间效率。

(2) 缺少初始定位策略。若当前y值下无法找到可行位置，对多边形在y方向上移动1个位置，进行横向可排放位置的搜索。而现实情况中，为了找到最终可行y值，可能要在y方向上移动多次，而且在每个y值下都要遍历所有扫描区间，进行重复且无用的扫描区间比较过程，如图2(e)所示。缺少y值定位策略的缺陷，增加了大量的算法过程中重复且无用的扫描区间比较过程，造成时间上不必要的浪费。

上述两个问题在过程中互相影响，也受y方向移动次数的增多等方面的影响，算法消耗的时间会越来越多，如图2(f)所示。

2 改进的快速扫描区间定位算法

2.1 算法设计

经过上述分析，提出两个优化上述问题的针对性方法。这里改变原料多边形扫描区间的内容，只记录原料空闲扫描区间，因而不存在脏位标记。

(1) 候选平移位置矩阵。包含多边形中所有扫描区间的可行移动距离。假设原料多边形为矩形，并且设定其宽度为W。待排多边形包围盒的长和宽分别为l和w；声明二维矩阵Span[l][w]，并初始化矩阵中所有值为 0，矩阵纵下标表示可移动距离，行下标表示当前行值，某位置的值表示该行满足该移动距离的扫描区间数。如 Span[i][j]=m表示第 i行有m个扫描区间可移动距离j；通过对矩阵列的累加值计算，可快速计算出x方向上最小可行移动距离。

统计待排多边形所有扫描区间数。在(1)方法确定y位置下，进行如下操作：

①计算候选平移位置矩阵：对多边形所有扫描区间查找可行移动距离，并更新可行矩阵对于位置的值，取其中某一扫描区间，其余同理。如图3所示（其中X1，X2，G1等标注代表该位置x值）。图中表示多边形扫描区间在原料对应行的可行移动距离区间有 3个，分别为（G1-X1，G2-X2）、（G3-X1，G4-X2）、（G5-X1，G6-X2）。则可将Span矩阵对应行的上述 3个区间所有位置的值加1，表示该位置可放下此多边形区间，同理对所有扫描区间进行上述计算过程。

②寻找最小可行移动距离：候选平移位置矩阵，从第一列开始，从上到下累加该列所有行的值，如果遇到某位置为 0，则表示该行没有扫描区间可以移动该距离，则该列无可行位置，从下一列开始重新累加。如果过程中未遇到 0，则比较最终的累加值和多边形总区间数是否相等，如果相等，则表示移动了该距离后，多边形所有区间都在原料空闲区间内；同时，计算时从左向右计算，找到的移动距离必然是最小可行移动距离。

(2) 最大跨度比较法。排放之前，分别求出待排多边形和原料多边形每行扫描区间的最大值，并且保存。多边形从原点出发，比较对应行最大区间值，若出现多边形中行最大值大于原料对应行空闲区间最大值，则该位置确定不可行，对y进行加1操作。此操作是一个粗定位过程，目的是过滤明显不符合排放条件的位置，经过这个操作，虽然无法保证剩下的位置一定可以满足排放条件，但是确实可以大量剔除掉一些不合理的位置，从而达到减少不必要的比较次数的效果，可有效避免图 2(d)和图2(e)的现象。

图3 可行移动距离区间

依据这些方面的算法改进思想，在原有算法的基础上，提出了一种更快速，更方便的算法，即基于扫描区间表示的不规则多边形快速定位算法，算法流程图如图4所示。

图4 快速扫描区间定位算法流程图

2.2 过程对比

为了更直观地展现快速扫描区间定位算法的优点，图5～6对同一待排多边形在不同算法下的轨迹作对比。要找到待排件2所在位置(如图5所示)，扫描区间定位算法沿着箭头反复进行扫描区间的比较和纵向移动的操作，其过程在时间上无疑是一种浪费。快速扫描区间定位算法依据行最大区间值比较排除法，尽快找到待排件2的所在位置，同时依据快速可行矩阵定位法，一次性计算出要到达正确位置2所要移动的距离(如图6所示)。过程显然优于扫描区间定位算法，在实际性能上也必然有所提高。

图5 扫描区间定位算法轨迹

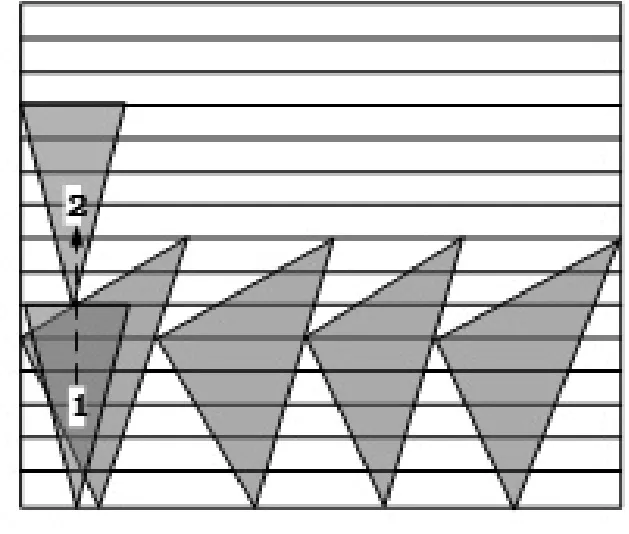
图6 快速扫描区间定位算法轨迹

3 实验与应用

本文算法已经在Microsoft Visual Studio 2008使用C++语言开发实现，并应用于作者所在小组与合肥汇锦数控设备制造有限公司联合开发的服装排料软件。本节的相关实验数据均是由合肥汇锦数控设备制造有限公司提供的实际数据，实验机器的配置如下：2.80 GHz Intel I5CPU，4.0 G内存。

相邻扫描线之间的距离对本文算法的精度和速度有重要影响，本文用每厘米中扫描线的数目(lines per centimeter, LPC)，表示刻画扫描线的疏密程度，那么布料的宽度、长度及衣片多边形的顶点坐标可按下式进行离散化：

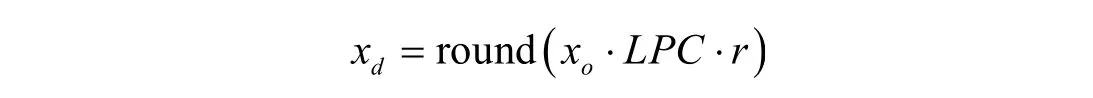
其中 xo表示原始宽度、长度或坐标，r表示原始长度单位与厘米之间的换算比率， round（·）表示四舍五入。本文算法采用离散化后的坐标 xd进行排料。

LPC越大则扫描线越精细，排料结果越精确，但因为需要进行更多的扫描线比较，则计算速度下降。本文中所有实验数据均为 PLT格式保存的衣片多边形文件，因为 PLT文件已经对衣片多边形等进行离散化，所以可直接采用测试文件的离散化结果，LPC的对应取值为400。本文分别选用含有 20、50、70、100个衣片模型的数据进行实验，使用本文方法和文献[12]的方法摆放衣片，摆放结果如图 7所示，原料利用率和时间消耗结果如表1所示。

实验结果表明本文算法对时间性能有明显改善，且衣片越多，效果越明显，这是因为衣片越多，原料上的空闲区域越复杂，本文的算法更有可能过滤更多的无效区域，从而更好地改善时间性能。每组实验结果是在相同的多边形序列，相同的原料宽度下，采用不同的算法进行。虽然排放序列的最终位置和材料利用率相同，但是时间消耗却大不相同。特别是在多边形个数增多的情况下，快速扫描区间定位算法能够在很大程度上提高时间效率。

图7 排料结果

表1 利用率及时间消耗表

4 结 论

排料问题在很多领域有广泛应用，但迄今为止还没有完全解决。二维不规则形状定位算法是排料问题的重要组成部分，本文通过深入分析获得广泛应用的基于扫描区间的二维不规则形状定位算法，从两个方面对其进行改进，从而实现了一种快速基于扫描区间的二维不规则形状定位算法，实验表明本文算法时间性能更优。

目前，本文仅基于最大跨度比较法排除一些不可能解，未来研究基于多边形面积等排除算法，以排除更多不可能解，从而进一步提高算法的效率。

[1] Hopper E, Turton B. A genetic algorithm for a 2D industrial packing problem [J]. Computers & Industrial Engineering, 1999, 37(1): 375-378.

[2] Baker B S, Coffman Jr E G, Rivest R L. Orthogonal packings in two dimensions [J]. SIAM Journal on Computing, 1980, 9(4): 846-855.

[3] 韩 珂. 智能优化排料方法研究[D]. 南京: 南京理工大学, 2009.

[4] 黄兆龙. 用启发算法和神经网络法解决二维不规则零件排样问题[J]. 微计算机信息, 2004, 20(7): 118-119.

[5] 贾志欣, 殷国富, 罗 阳. 二维不规则零件排样问题的遗传算法求解[J]. 计算机辅助设计与图形学学报, 2002, 14(5): 467-470.

[6] 陈 勇, 唐 敏, 童若锋, 董金祥. 基于遗传模拟退火算法的不规则多边形排样[J]. 计算机辅助设计与图形学学报, 2003, 15(5): 598-603.

[7] 李 明, 宋成芳, 周泽魁. 二维不规则零件排样问题的粒子群算法求解[J]. 江南大学学报(自然科学版), 2005, 4(3): 266-269.

[8] Li Aiping, Zhang Feng, Liu Xuemei. Range box-based algorithm for optimal blank layout [J]. Computer Engineering and Applications, 2007, 43(1): 198-200.

[9] 李 明, 张光新, 周泽魁. 基于改进遗传算法的二维不规则零件优化排样[J]. 湖南大学学报(自然科学版), 2006, 33(2): 48-50.

[10] Art R C. An approach to the dimensional irregular cutting-stock problem [R]. IBM Cambridge Scientific Center report 36-Y08, Cambridge: IBM Cambridge Scientific Center, 1966.

[11] Adamowicz M, Albano A. Nesting two-dimensional shapes in rectangular modules [J]. Computer-Aided Design, 1976, 8(1): 27-33.

[12] 陈 勇. 二维不规则形优化排样技术研究[D]. 杭州:浙江大学, 2003.

Scan Region Representation Based Fast Irregular Polygon Position Algorithm and Its Application

Luo Yuetong, Lv Shi, Jiang Yuqing
(VCC Division, School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China)

Irregular polygon position algorithm is an important part of nesting algorithm, and it has great influence on nesting algorithm′s performance. Scan region representation based fast irregular polygon position algorithm is widely applied for it can process complex polygon, but it has shortcoming of huge computation. By intensively analyzing the algorithm, the paper improves it in two ways: the paper firstly presents the concept of candidate position matrix to realize fast position scan algorithm; and impossible rows are fast picked out through maximum span cooperation, so that the algorithm is further accelerated by avoid calling position scan algorithm for impossible rows. The algorithm has been applied in self-developed cloth nesting software, several real cloth designs are used to test the algorithm, and the result demonstrates the algorithm′s effectiveness and efficiency.

nesting; scan region representation; irregular polygon; position algorithm

TP 391

A

2095-302X(2014)06-0815-06

2014-05-29；定稿日期：2014-07-25

国家自然科学基金资助项目(11305205；61370167；61305093)

罗月童(1978-)，男，安徽青阳人，副教授，博士。主要研究方向为科学计算可视化、计算机图形学和计算机辅助设计。E-mail：ytluo@hfut.edu.cn