基于序列模型的三维矩形布局算法

王金敏， 朱丽苹

（1. 天津市高速切削与精密加工重点实验室，天津 300222；2. 天津职业技术师范大学机械工程学院，天津 300222）

基于序列模型的三维矩形布局算法

王金敏1,2， 朱丽苹2

（1. 天津市高速切削与精密加工重点实验室，天津 300222；2. 天津职业技术师范大学机械工程学院，天津 300222）

针对三维矩形布局问题进行了研究。在三元序列的基础上，结合布局物体的几何可行域，提出了三元序列结合几何可行域的布局算法。并且利用遗传算法对布局算法进行优化，得到了三元序列结合可行域布局遗传算法。分析和实例证明，三元序列结合几何可行域的改进算法有效地提高了布局效率。

布局问题；三元序列；可行域；遗传算法

布局问题(packing problem)[1-2]是指给定一个布局空间和若干待布物体，将待布物体合理地摆放在空间中满足必要的约束，并达到某种最优指标。布局问题的求解非常困难，唐晓君等[3]详细阐述了布局问题的复杂性。即使是最简单的一维布局问题也被证明是 NP完全问题(non-deterministic polynomial, NP)。因此，布局问题吸引了大批的学者对其进行研究。Hashimshony和 Roth[4]介绍了ALG模型，该模型在给定的约束条件下，利用图论来产生可行的布局方案。袁苗龙等[5]利用图法则分析了三维布局模型生成方法对车身内进行了布置，但文章并没有过多地对布局结果进行分析。晏敏等[6]给出了用于表达矩形物体平面布局空间关系的方图模型，并提出了方图矩阵及其运算规则。该模型侧重平面布局问题的求解，对空间布局问题的求解有一定的困难。吴慧中等[7-8]利用空间布局的约束图方法对房间布局进行了初步试验，证明约束图在处理布局问题时比其他模型更简便、高效，文章只是停留在试验阶段，对该方法解决问题的能力有待进一步阐述。

此外，许多学者利用启发式优化算法求解布局问题，取得了不错的结果。Lai和Chan[9-10]利用模拟退火算法和遗传算法对布局问题进行求解。解空间是待布物体的排列，一个解表示一个布局。但是文章只给出了有限的几个解。Beasley[11]在遗传算法的基础上提出了一个能有效解决4000块待布物体的启发式算法。但是对已知最优解的小算例该算法却不能取得最优解。Egeblad和Pisinger[12]提出了一个整数规划方程式，并在此基础上仿照Murata等[13]提出解决二维布局问题序列的方法，给出了一个由三元序列表示三维装箱问题的布局算法，并用模拟退火算法优化三元序列。但是文章没有对由三元序列表示的布局结果进行进一步改善处理。本文在三元序列的基础上，结合可行域，对原布局算法进行了改善，之后再用遗传算法对此布局算法进行优化。

1 三元序列模型

文献[12]介绍了利用三元序列模型求解布局问题，此模型属于图论模型的范畴。大部分的布局可以用这个方法表示，其中具有代表性的是“机器人码垛”，根据“机器人码垛”的定义，总会有一个布局物体被放置在布局空间的最左、最下和最后的角点。“机器人码垛”是从空间的左下后角点开始，依次布入布局物体，这样，每布入一个布局物体都会在前一个已步入的布局物体的右面、上面、前面。

1.1 三元序列

lij(left)、rij(right)、uij(under)、oij(over)、bij(behind)和fij(front)分别表示布局物体i在j(i＜ j)的左面、右面、下面、上面、后面和前面。为了确保布局物体i和j不发生干涉，应满足如下不等式：

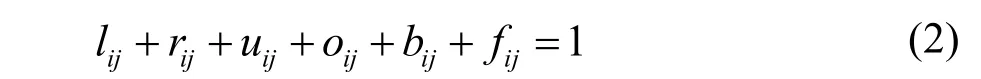
当 si= sj=1, lij, rij, uij, oij, bij, fij要满足如下的不等式：

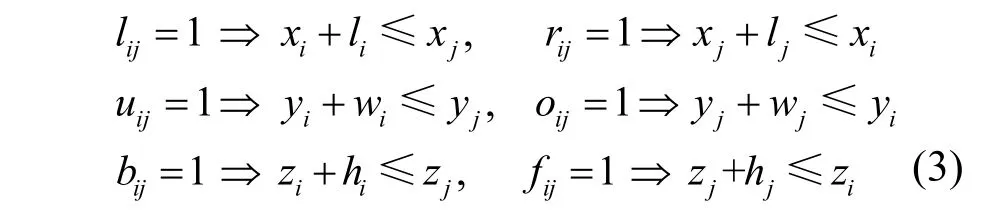
对于三维布局问题，可用一个三元序列A，B和C来表示，每一个序列都是n个布局物体的排列。对于每一个序列X，Xij表示：在序列X里，布局物体i在j之前。

为了方便起见，令 - Xij⇔ Xji。

也就是说 Aij表示布局物体i在布局物体j的左面、上面或前面。

也就是说 Bij表示布局物体i在布局物体j的左面、下面或后面。

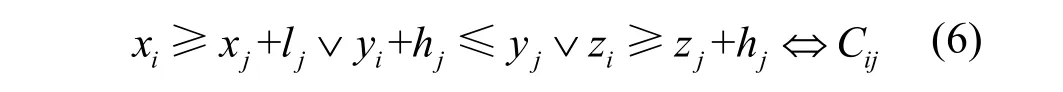
也就是说 Cij表示布局物体i在布局物体j的右面、下面或前面。

1.2布局算法

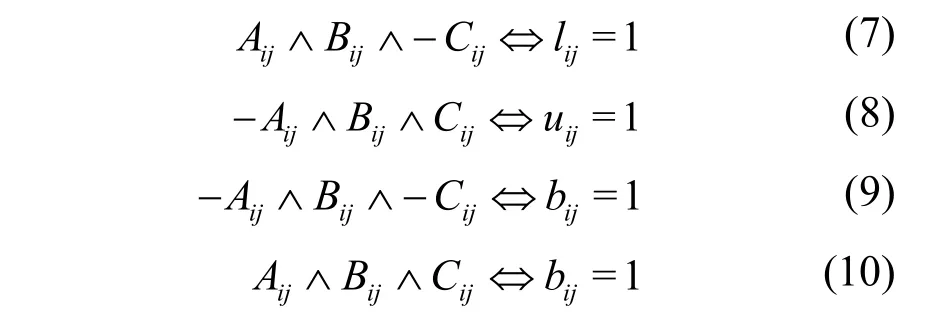
三元序列到布局，要建立3个约束图。第一幅图中，i到j的边表示布局物体i在j的左边，即第二幅图中，i到j的边表示布局物体i在j的下边，即第三幅图中，i到j的边表示布局物体i在布局物体j的后边，即

在每一幅约束图当中，Bij都是i在j之前的必要条件。因此，可以按照序列 B的顺序布局。序列B中的第一块待布物体放置在(0,0,0)，依次按照B序列中的排序布局。为了便于记录，在布局过程中建立一个集合P，令P包含所有已布入的布局物体。子集 Px⊆ P， Px中的布局物体满足约束子集中的布局物体满足；子集中的布局物体满足若对布局物体 i进行布局，为了确定i的布局位置，要把i依次和P中布局物体比较。布局物体i的坐标(xi, yi,zi)可由如下方程求解：

一旦布局物体i被放置在布局空间中，它就加入到集合P中。文献[12]给出一个布局算例，其布局物体长、宽、高尺寸如表1所示。

由三元序列A = (9, 4, 8, 5, 1, 6, 2, 7, 3)，B = (7, 8, 6, 9, 1, 3, 5, 2, 4)，C = (2, 3, 6, 7, 1, 4, 5, 9, 8) 得到的布局结果（见表2），布局结果如图1所示。

表1 布局物体的长宽高

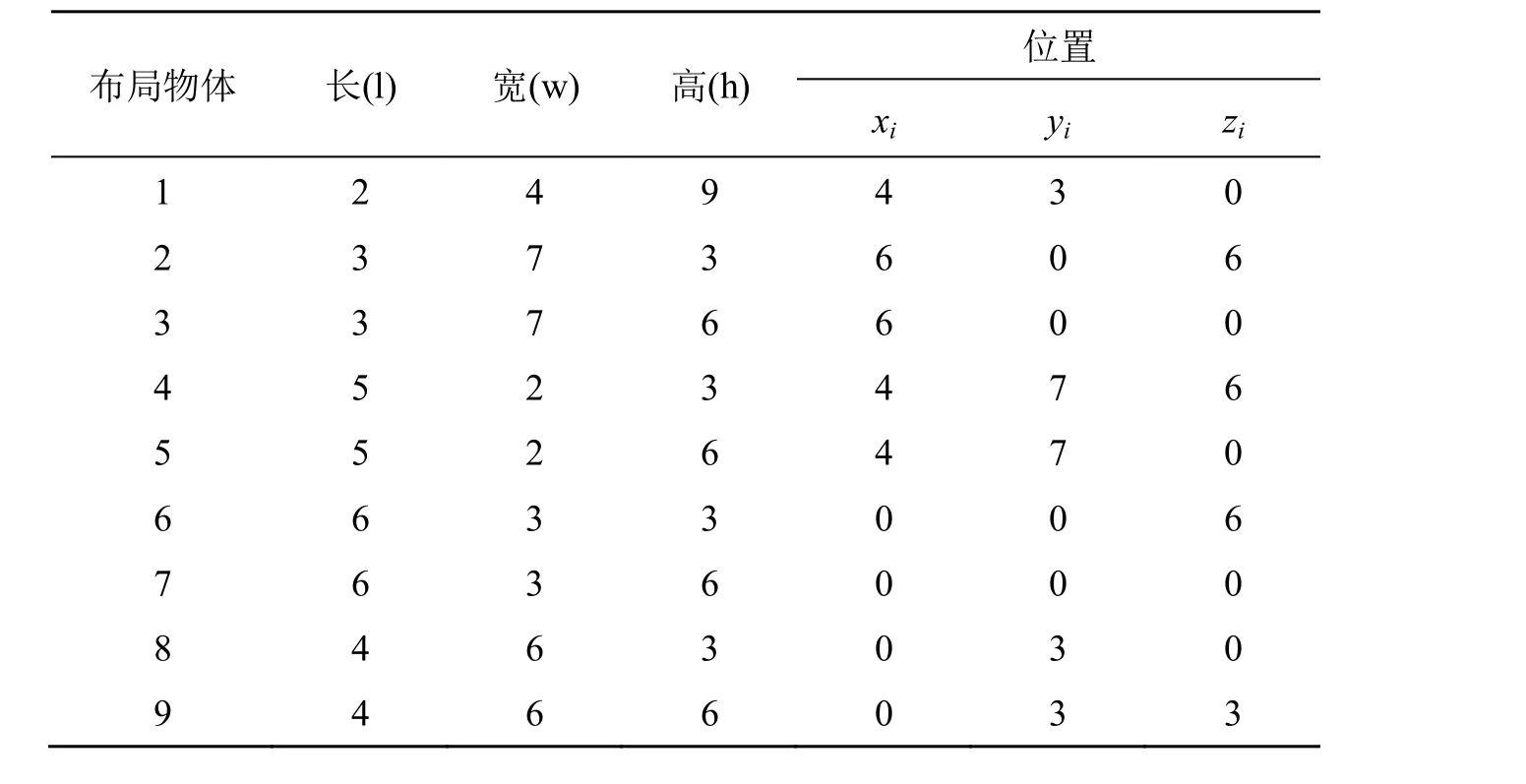
表2 布局物体的长宽高及布置位置

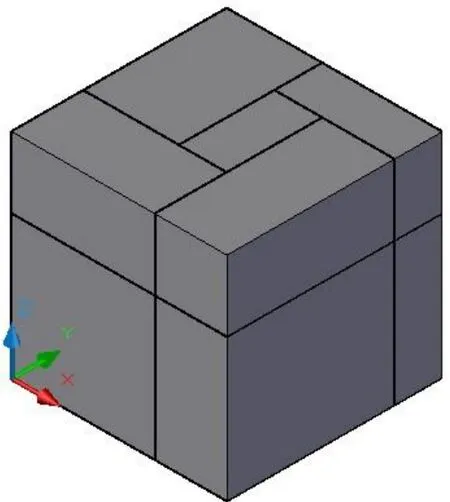
图1 文献[12]给出的布局结果

1.3 分析

对文献[12]进行分析可知：

(1) 文献[12]指出lij+ rij+ uij+ oij+ bij+ fij= 1，但根据实际的布局情况，如果布局物体i既在布局物体j的前面，同时又在j的左面和上面，则有lij+rij+uij+oij+bij+fij= 3。本文将其改为：

(2) 文献[12]指出 + + x xl y yh z

i ji i ji i≤ ˇ≤ ˇ≤zh ⇔B

j i ij +，本文将其改为：

(3) 由三元序列A = (9, 4, 8, 5, 1, 6, 2, 7, 3)， B = (7, 8, 6, 9, 1, 3, 5, 2, 4)，C = (2, 3, 6, 7, 1, 4, 5, 9, 8)得出的布局结果如图2所示，图1所示的三元序列应为A = (9, 4, 8, 5, 1, 6, 2, 7, 3)，B = (7, 6, 8, 9, 1, 3, 2, 5, 4)，C = (2, 3, 6, 7, 1, 4, 5, 9, 8)。

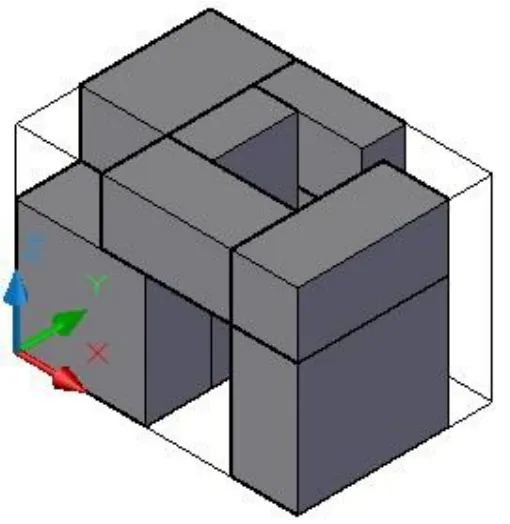
图2 实际的布局结果

2 三元序列结合可行域改进算法

文献[12]的算法虽然能达到一定的布局效果，但是由算例结果来看，布局效果并不是非常理想。因此，本文在此算法的基础上做出了改进，每一个待布局物体由三元序列确定了一个布局位置（一个点）之后，再把可行域内的其他点与三元序列确定的点进行比较，比较这些点与上一个已布入的布局物体的距离，选择距离最小的点作为待布局物体的布局位置。可行域的求法见文献[14]。原算法和改进的布局算法基本流程图分别如图3和图4所示。

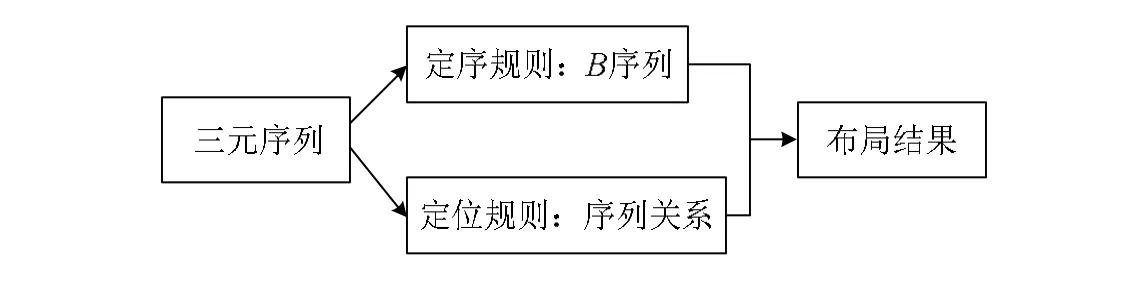
图3 原布局算法的基本流程

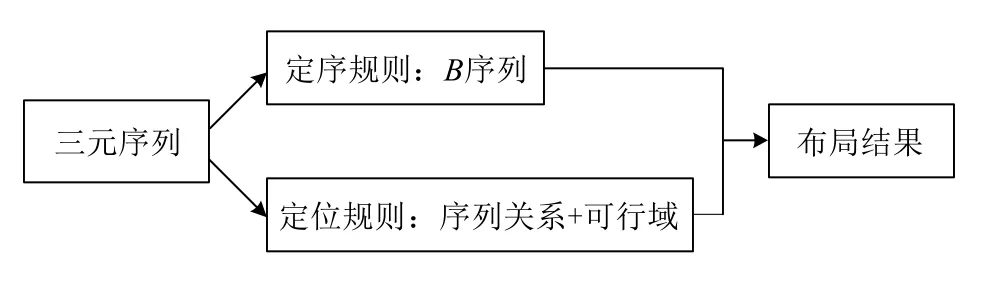
图4 改进布局算法的基本流程

本文利用遗传算法对三元序列进行优化。

2.1 编码策略

本文直接对优化变量采用实数编码。每个染色体由A、B、C 三个序列构成，基因0～n-1（包括0和n-1）表示序列A，基因n～2n-1（包括n和2n-1）表示序列B，基因2n～3n-1（包括2n和3n-1）表示序列C。因此每个染色体都有3n个基因，基因的个数随着待布局物体的个数变化而变化。

2.2 适应度函数及初始种群的产生

本文中的初始候选解由计算机随机产生，每个候选解就是一个个体，这些个体构成了初始种群。适应度函数f是评价各解优劣的标准。本文适应度函数选为布局空间的体积利用率，即：

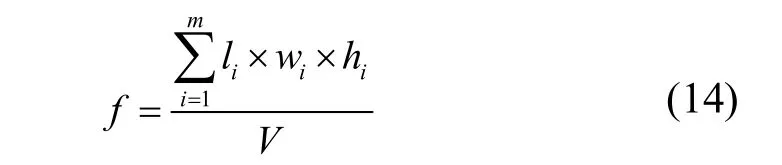
2.3 选择算子

选择操作就是从种群中选择两个候选解，以便进一步操作。本文使用蜜蜂进化选择算子，其具体实现如下：

2.4 交叉算子

(1) 将父代染色体的序列 B的基因（基因n+1～2n）全部交换。

将父染色体A和C序列的基因直接复制到子代解1的A和C序列部分，子代解1的B序列由母染色体的B序列填充；

将母染色体A和C序列的基因直接复制到子代解2的A和C序列部分，子代解2的B序列由父染色体的B序列填充。

(2) 将父代染色体的序列B的基因部分交换，进行单点交叉。

随机产生一个n+1～2n的交叉点，父染色体B序列在交叉点左侧的代码直接复制到子代解 1的左侧，子代解 1交叉点右侧的代码依次从母染色体选择未在子代解 1中使用的代码。父染色体 A序列和C序列直接复制到子代解1的A序列和C序列。交叉过程如图5所示。

(3) 将父代染色体的序列A的基因部分交换，进行两点交叉。

随机产生两个1～n的交叉点p1和p2，父染色体A序列在交叉点p1左侧的代码和p2右侧的代码直接复制到子代解 1的左侧和右侧，子代解 1的两交叉点中间的代码依次从母染色体中选择未在子代解1中使用的代码。父染色体B序列和C序列直接复制到子代解1的B序列和C序列。交叉过程如图6所示。

图5 序列B单点交叉

图6 序列A两点交叉

2.5 变异算子

(1) 随机交换染色体A序列和B序列中两个代码的位置。

随机产生一个[1, n]的数k1，一个[n+1, 2n]的数k2，交换k1和k2所对应的代码。将A序列中与交换后的代码相同的基因位处，用 A序列未使用过的代码替换；如果k1和k2所对的代码相同，则重新产生随机数直到k1和k2所对应的代码不相同为止。变异过程如图7所示。

(2) 随机交换染色体B序列和C序列中两个代码的位置。方法同(1)。

3 算例及分析

算例1.采用文献[12]中的三维算例ep-3d。此类算例共包括60个三维装箱问题。布局物体的个数分别为20，40，60。表3将文献[12]算法和本文算法求出的布局结果进行了比较。

图7 序列A和序列B之间的变异

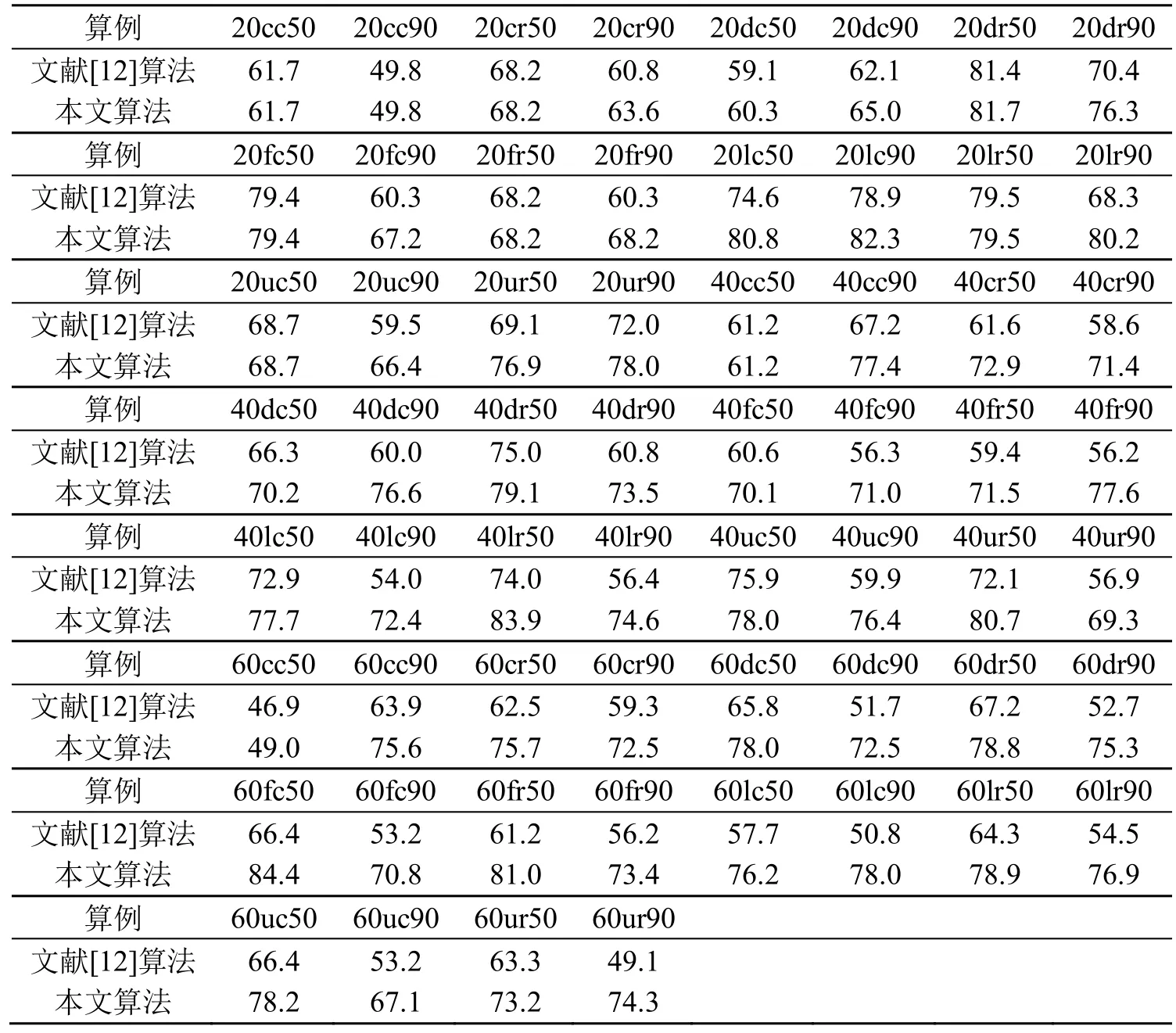
表3 文献[12]算法与本文算法布局结果比较(%)

由表3可以看出，本文算法较文献[12]算法有了很大地提高，利用率平均提高了10.24%。最差的结果也保持与文献[12]算法的结果相等，而对于提升幅度最高的算例60lc90利用率则提高了27.2%。对于算例60lc90两种算法的布局效果如图8所示。图 8中文献[12]算法中布局物体之间的空隙比较大。这是由三元序列本身原因造成的，所以本文对由三元序列布局的结果进行处理，即与布局物体几何可行域结合，寻找待布局物体最优的布局位置。算例20lc90、40ur50、60uc50的布局结果与Jens的布局结果比较如图9～11所示。可以看出本文算法有效地提高了布局空间的利用率。

算例2.此算例由二维C类算例改进而来，在原有的算例基础上，对布局空间和布局物体都增加了同样的高。C1～C7算例中布局物体数量逐渐增多。C11～C13算例当中总共有16块布局物体，C71～C73当中总共有196块布局物体。表4将本文算法求出的布局结果和文献[12]算法求解的结果进行了比较。两种算法对 C类算例的计算结果的对比如图12。

图8 文献[12]算法(左)与本文算法(右)的布局结果

图9 算例20lc90本文算法(左)与文献[12]算法(右)的布局结果

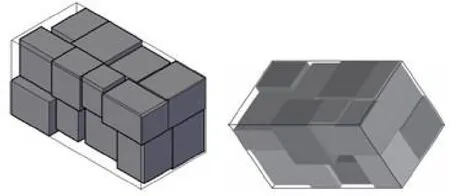
图10 算例40ur50本文算法(左)与文献[12]算法(右)的布局结果

图11 算例60uc50本文算法(左)与文献[12]算法(右)的布局结果

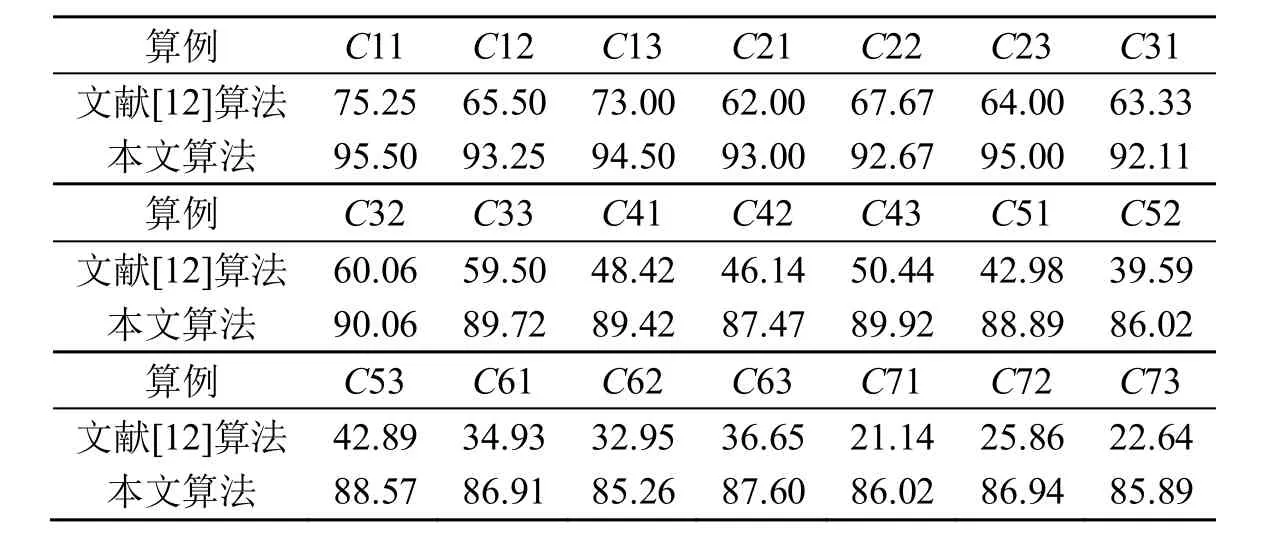
表4 文献[12]算法与本文算法对C类算例布局结果比较(%)

图12 两种算法对C类算例的计算结果

由表4的数据可以看出，对于C11算例布局空间利用率提高了 20.25%，C71算例提高了64.88%，所有算例平均提高了40.47%。

由图12可以看出，随着布局物体数量的增多，本文算法的利用率有所下降，文献[12]算法的利用率则呈现显著下降的趋势。这是因为随着布局物体的增多，布局物体之间的空隙也就越来越多，从而造成布局空间体积的浪费。这说明，文献[12]算法只适用于布局物体数量较少的算例，而本文算法在布局物体数量较多的算例中同样能表现出较好的性能。

4 结 束 语

本文对文献[12]提出的三元序列进行了分析，提出了一种以三元序列为基础，结合几何可行域的改进布局算法，并用遗传算法来优化布局物体的布局顺序。最后分别用文献[12]算法和本文布局算法对两组算例进行了计算、比较，实例证明，三元序列结合几何可行域的改进算法有效地提高了布局效率。

[1] Sweeny P E, Paternoster E R. Cutting and packing problems: a categorized, application-orientated research [J]. Journal of Operation Research Society, 1992, 43(7): 691-706.

[2] Dowsland K A, Dowsland W B. Packing problems [J]. European Journal of Operational Research, 1992, 56(1): 2-14.

[3] 唐晓君, 査建中, 陆一平. 布局问题的复杂性和建模方法[J]. 北方交通大学学报, 2003, 27(1): 12-15.

[4] Hashimshony R, Roth J. ALG: a model for generating alternative layout graphs under architectural constraints [J]. Computer Aided Design, 1986, 18(8): 431-436.

[5] 袁苗龙, 胡于进, 付莉红. 基于图法则分析的三维布局模型生成方法[J]. 华中理工大学学报, 1998, 26(10): 38-41.

[6] 晏 敏, 张昌期, 刘育骐. 平面布局的一个拓扑模型:方图[J]. 小型微型计算机系统, 1989, 10(2): 23-32.

[7] 吴慧中, 王英林. 一种立体空间布局模型及布局算法[J]. 计算机学报, 1994, 17(11): 835-840.

[8] 王英林, 吴慧中, 田宜风. 求解布局模型的并行矩阵算法研究[J]. 计算机辅助设计与图形学学报, 1998, 10(4): 341-348.

[9] Lai K K, Chan J W M. Developing a simulated annealing algorithm for the cutting stock problem [J]. Computers and Industrial Engineering, 1997, 32(1): 115-127.

[10] Lai K K, Chan J W M. A evolutionary algorithm for the rectangular cutting stock problem [J]. International Journal on Industrial Engineering, 1997, 4(1): 130-139.

[11] Beasley J E. A population heuristic for constrained two-dimensional non-guillotine cutting [J]. European Journal of Operational Research, 2004, 156(3): 601-627.

[12] Egeblad J, Pisinger D. Heuristic approaches for the two and three dimensional knapsack packing problem [J]. Computers & Operations Research, 2009, 36(4): 1026-1049.

[13] Murata H, Fujiyoshi K, Nakatake S, Kajitani Y. VLSI module packing based on rectangle-packing by the sequence pair [J]. IEEE Transaction on Computer Aided Design of Integrated Circuits and Systems, 1996, 15(12): 1518-1524.

[14] 朱丽苹, 王金敏. 基于空间分割的求解布局几何可行域的算法[J]. 天津职业技术师范大学学报, 2012, 22(2): 30-33.

An Improved Algorithm for 3D Rectangular Packing Sequence Model

Wang Jinmin1,2, Zhu Liping2
(1. Tianjin Key Laboratory of High Speed Cutting & Precision Machining, Tianjin 300222, China; 2. School of Mechanical Engineering, Tianjin University of Technology and Education, Tianjin 300222, China)

This paper studies the three dimensional rectangular packing problem. On the basis of sequence triple, combined with geometry feasible region of packing items, the sequence triple and feasible region packing algorithm is proposed. Then the packing algorithm is optimized by genetic algorithm, the sequence triple and feasible region packing genetic algorithm is formed. Analysis and examples prove that the improved sequence triple and feasible region packing algorithm can effectively increase packing efficiency.

packing problem; sequence triple; feasible region; genetic algorithm

TP 391

A

2095-302X(2014)06-0821-07

2013-04-19；定稿日期：2013-05-29

国家自然科学基金资助项目(60975046)；天津职业技术师范大学科研发展基金资助项目(KJ14-64)

王金敏(1963-)，男，河南舞阳人，教授，博士。主要研究方向为智能布局、计算机辅助设计及图形学。E-mail：wang_jin_min@163.com