Cournot-Bertrand双寡头动态博弈模型的复杂性分析

何岩岩，张 芳

（天津工业大学理学院，天津 300387）

Cournot-Bertrand双寡头动态博弈模型的复杂性分析

何岩岩，张 芳

（天津工业大学理学院，天津 300387）

提出了一个主从的Cournot-Bertrand双寡头混合博弈模型.寡头都是在有限理性期望下进行的博弈，并且上级寡头考虑产量，下级寡头考虑价格.分析了该模型的纳什均衡点和它的局部稳定性.通过数值模拟，利用稳定域图、分岔图、最大Lyapunov指数图以及奇异吸引子图研究了该模型的复杂动力学性质，且通过分析两寡头的利润分岔图，得出了均衡态是二者都满意状态的结论.

主从；Cournot-Bertrand；有限理性；复杂动力学；动态博弈模型

寡头市场是一个市场被少数几个企业垄断的市场结构.研究寡头竞争的模型一般有考虑产量竞争的Cournot模型和考虑价格竞争的Bertrand模型，目前，已经有很多专家和学者对此进行了大量的研究，参见文献[1-6].Puu[1]把两寡头Cournot模型推进到了三寡头的情形，发现了比两寡头博弈更多样的分岔现象.也有一部分学者对同时考虑寡头产量和价格的Cournot-Bertrand混合模型进行了研究.Ma等[7]通过对双寡头Cournot-Bertrand混合模型动力学性质的研究，发现产量调整速度和价格调整速度过快都可以引起市场进入对两寡头都不利的混沌状态.以上文献都是致力于研究横向水平的寡头竞争，而对于纵向水平寡头竞争的研究较少，并且这类寡头竞争在经济市场中普遍存在.Xin等[8]以自来水与纯净水厂商为例，建立了一个主从的Bertrand双寡头博弈模型.他们把自来水公司作为上级寡头，纯净水公司为下级寡头，制定了具有同样期望的动态价格决策.通过数值模拟及分析，证明了系统存在分岔和混沌等复杂动力学性质，并且说明了价格的波动会带来一定的价格风险，然而并没有对公司的利润作出分析.本文在该模型的基础上，研究了主从的混合Cournot-Bertrand双寡头模型.在该模型中，上级寡头考虑产量，下级寡头考虑价格.通过对该模型的动力学性质的分析及对这两寡头整体利润的研究，可以对这类寡头市场的运行提供引导的作用.

1 模型

假设市场上有2个异质寡头，公司i生产商品xi，i=1，2.代表上级寡头的公司1在产量方面进行竞争，代表下级寡头的公司2在价格方面进行竞争.在主从寡头博弈中，由于上级公司的产量是下级公司产量决策的主要因素，而作为上级公司产品的一个较小的消费个体，下级公司对上级公司的产量影响很小，可以忽略不计.在该假设下，公司1和2的需求函数可设为

式中：p1（t）、p2（t）分别表示公司1、2在t期的价格；d表示产品的差异化指数或产品替代率；且a，b，a2，b2，d>0.根据第一个等式，公司1的价格可以表示成

考虑这2个公司的成本函数为线性：

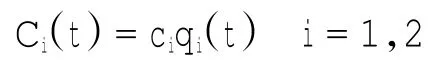
这里ci表示公司i的边际成本，且ci>0.则这2个寡头公司的利润为

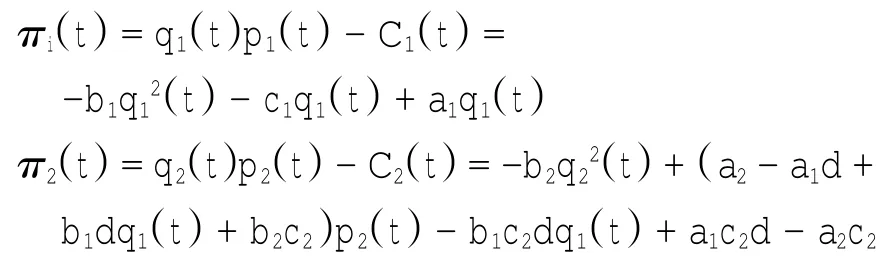
设这2个公司对市场和对手只能获得有限的信息处理能力.在博弈中，两寡头按照有限理性的期望进行调整并根据边际利润制定决策.即如果边际利润为正（负）时，它们将分别增加（减少）下期的产量和价格.这两个公司的边际利润如下：

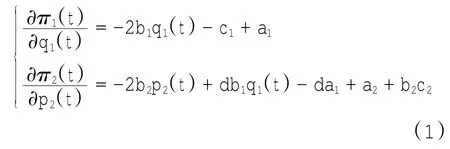
在上述假设下，这个主从博弈的动态模型为

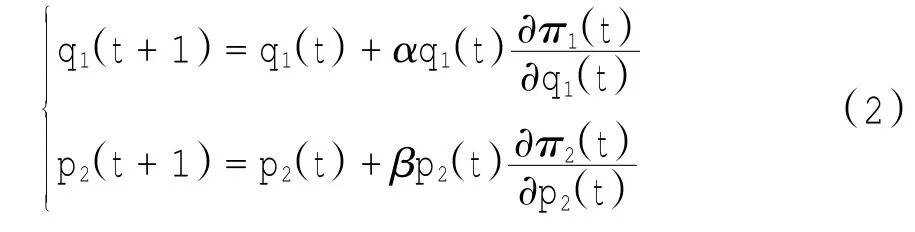
将方程组（1）代入到方程组（2）中，则该模型有如下形式：

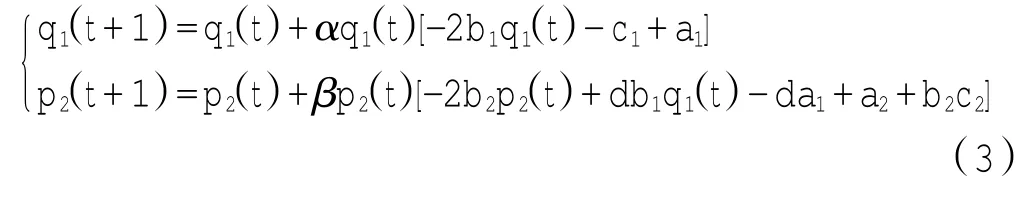
2 均衡点和稳定性

系统（3）有4个非负均衡点：E0=（0，0），E1=（0，其中且为了讨论系统（3）关于状态变量（q1，p2）的稳定性，给出这4个均衡点的Jacobian矩阵J.

则E0的Jacobian矩阵为

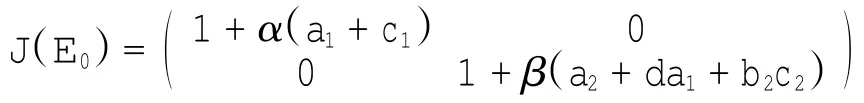
它的特征值λ1=1+α（a1-c1），λ2=1+β（a2-da1+b2c2）.要使E0稳定必须有|λ|<1，由于显然λ1>1，λ2>1，均衡点E0是不稳定的结点.

E1的Jacobian矩阵J为

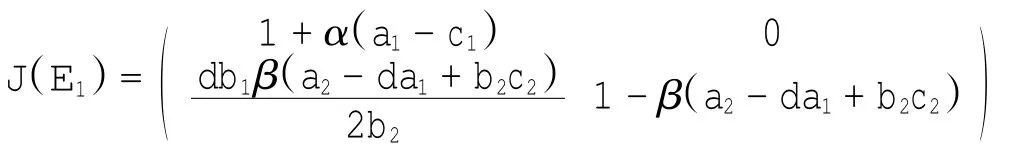
则λ1=1+α（a1-c1），λ2=1+β（a2-da1+b2c2）.在所有均衡点非负的前提下，得到λ1>1.故均衡点E1不稳定.类似地，可证均衡点E2不稳定.

E*为纳什均衡点，它的Jacobian矩阵为

J（E*）的特征方程为P（λ）=λ2-Tr（J（E*））λ+Det（J（E*））=0，其中Tr（J（E*））和Det（J（E*））分别表示J（E*）的迹和行列式.

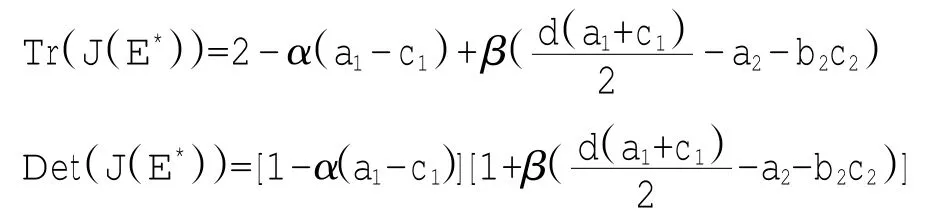
用研究离散的二位系统稳定性条件的方法来讨论系统（3）的纳什均衡点的稳定性，该条件被称为Jury条件，参见文献[9-10]：

以上不等式组确定了纳什均衡点E*的局部稳定域.通过求解以上3个不等式，得到，当且a2>或者，局部稳定域为

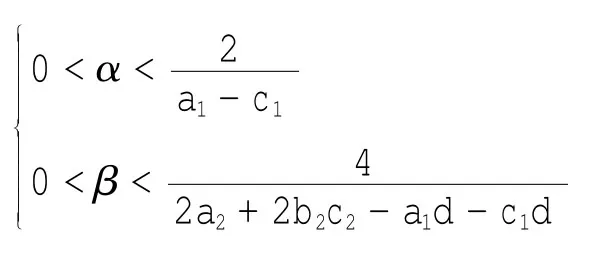
3 数值模拟

在这部分用稳定域、分岔图、最大Lyapunov指数、奇异吸引子来探索系统（3）的动力学行为.为了研究纳什均衡点的局部稳定性，取下面的参数值：a1=1，a2=1，b1=1，b2=1，c1=0.1，c2=0.1，d=0.2，初始值取（q1（0），p2（0））=（0.2，0.1）.

图1为参数取以上值时，纳什均衡点E*的稳定域.从图1可以看出，使得E*稳定的区域是矩形域0≤α<2.222，0≤β<0.02.

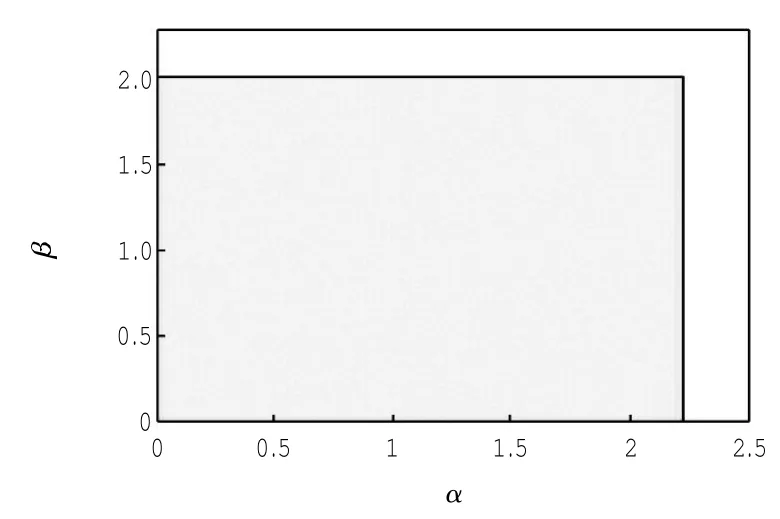
图1 纳什均衡点稳定域Fig.1 Nash equilibrium region of stability

图2给出了β=1时，公司1的产量及公司2的价格关于α演化的分岔图.其中，q1表示公司1的产量变化图，P2表示公司2的价格变化图.在给定以上参数值得情况下，发现当α>0时，Jury条件的（ii）和（iii）显然满足，随着α的增加，系统（3）会跳出条件（i）确定的范围，故该系统会产生flip分岔，见文献[12].在图2中，当α<2.222时，系统（3）中的点稳定在纳什均衡点Ε*=（0.45，0.495）.随着α增加，两寡头的行为变得不稳定并且复杂动力学行为产生.可以看出二倍周期分岔产生在α=2.222，随后两寡头行为进一步复杂，在α>2.855时，系统（3）进入混沌.图3给出了当其他参数不变，α=1时，公司1的产量及公司2的价格关于β演化的分岔图.从图3可以看出，公司1始终处于稳定状态，公司2在β=2.02时，产生分岔行为，在β= 2.596时，进入混沌.

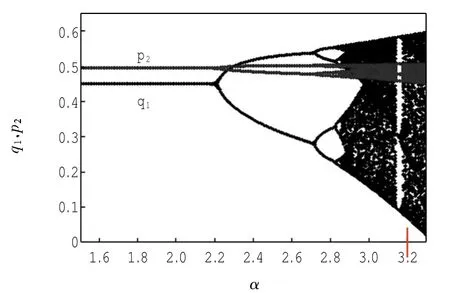
图2 q1、p2随α演化的分岔图Fig.2 Bifurcation diagrams of q1and p2with respect to α

图3 q1、p2随β演化的分岔图Fig.3 Bifurcation diagrams of q1and p2with respect to β

比较图2和图3，公司1产量的调整速度对两公司行为均有影响，公司2的价格调整速度对公司1没有影响，并且公司2对β的表现出较强的敏感性.从而可以得到以下结论：①较之于上级寡头公司产量的变动，该系统对下级寡头的价格的变动较为敏感；②上级寡头产量的变动对系统整体的影响较为明显.

为了分析倍周期及混沌产生时的参数，给出了系统关于α变化的最大Lyapunov指数及奇异吸引子图，如图4所示.

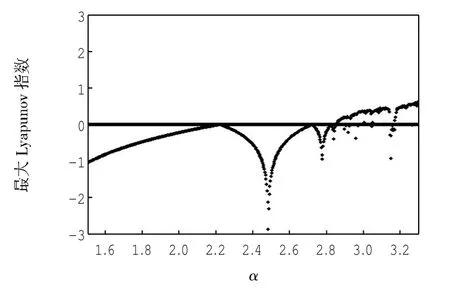
图4 最大Lyapunov指数Fig.4 The largest Lyapunov exponent

从图4可以看出，在α=2.222时，最大Lyapunov指数为0，此时系统进入二倍周期分岔.而在α=2.855时，指数为正，说明系统开始进入混沌.图5为当其他参数不变，α=3.1，β=1时系统（3）的奇异吸引子图，再次展示了该系统的分形结构.

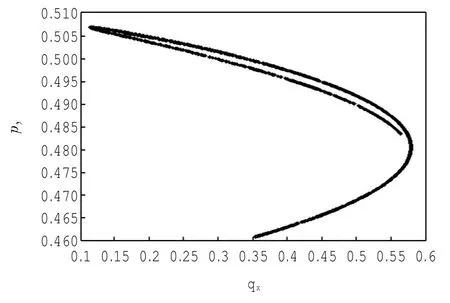
图5 α=3.1，β=1时的奇异吸引子结构Fig.5 Strange attractor for α=3.1，β=1

为了更好地分析该模型的实际意义，图6给出了两寡头随α变化的利润分岔图.

图6 关于α的利润分岔图Fig.6 Bifurcation diagrams of the profit with respect to α

图6中：π1表示的是公司1的利润；π2表示的是公司2的利润.该分岔图和图2相对应.显然公司1的利润在整体上大于公司2的利润，这说明作为上级寡头的公司比下级寡头公司在竞争中更有优势.当α= 2.222时，即在稳定域内，公司1的利润高于其进入周期分岔及混沌区域的利润，并且进入混沌后，利润变得无法估计，显然均衡态是其满意状态.而公司2在进入混沌后，不能明显看出它是在均衡态还是在混沌状态更有优势，然而由于混沌状态具有很多不确定性，且公司2在混沌状态时的利润整体没有高于它在均衡态的利润，所以参与者一般对均衡态的表现较为满意.总之，均衡态是这2个寡头都较为满意的状态.

4 结束语

本文对主从的Cournot-Bertrand双寡头竞争模型进行了分析，研究了该模型的稳定和分岔情况，并且分析了表明系统进入混沌的最大Lyapunov指数及奇异吸引子，最后给出了两寡头的利润随调整参数的演化图，得出了均衡态是两寡头都满意状态的结论.

[1]PUU T.Complex dynamics with three oligopolists[J].Chaos，Solitons&Fractals，1996，7：2075-2081.

[2]AGIZA H N.On the analysis of stability，bifurcation，chaos and control of Kopel map[J].Chaos，Solitons&Fractals，1999，10：1909-1916.

[3]BISCHI G I，NAIMZADA A.Global analysis of a dynamic duopoly gamewith bounded rationality[C]//Advances in Dynamic Games and Application.Basel：Birkhauser，2000：361-385.

[4]AGIZA H N，HEGAZI A S，ELSADANY A A.Complex dynamics and synchronization of duopoly game with bounded rationality[J].Mathematics and Computers in Simulation，2002，58：133-146.

[5]TRAMONTANA F.Heterogeneous duopoly with isoelastic demand function[J].Economic Modelling，2010，27：350-357.

[6]AGIZA H N，ELSADANY A A.Chaotic dynamics in nonlinear duopoly game with heterogeneous Players[J].Applied Mathematics and Computation，2004，149：843-860.

[7]MA Junhai，PU Xiaosong.The research on Cournot-Bertrand duopoly model with heterogeneous goods and its complex characteristics[J].Nonlinear Dyn，2013，72：895-903.

[8]XIN Baohui，CHEN Tong.On a master-slave Bertrand game model[J].Economic Modelling，2011，28：1864-1870.

[9]PUU T.Attractors，Bifurcations&Chaos：Nonlinear Phenomena in Economics[M].New York：Springer，2003.

[10]DU Jianguo，FAN Yueqian.Dynamics analysis and chaos control of a duopoly game with heterogeneous players and output limiter[J].Economic Modelling，2013，33：507-516.

Complexity analysis of a master-slave Cournot-Bertrand duopoly dynamic game model

HE Yan-yan，ZHANG Fang
（School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

A master-slave Cournot-Bertrand duopoly game model is presented.The two monopolists carry out the game with the expectation of bounded rationality and the upstream monopolist considers its output while the downstream monopolist considers its price.The existence of Nash equilibrium point and its local stability of the game are investigated.The complex dynamics，such as the graph of stability region，bifurcation diagrams，the maximal Lyapunov exponents diagram and strange attractor figure are displayed.It is found that equilibrium state is satisfaction to them both by analyzing the profits bifurcation diagram of the two oligarchs.

master-slave；Cournot-Bertrand；bounded rationality；complex dynamics；dynamic game model

O225

A

1671-024X（2014）03-0080-04

2013-10-24

国家自然科学基金资助项目（11071279）

何岩岩（1989—），女，硕士研究生.

张 芳（1974—），女，博士，副教授，硕士生导师.E-mail：zhangfangsx@163.com