基于遗传算法的可逆逻辑综基合于方法及其CUDA并行化实现
2014-03-15陈丽萍王子丹赵曙光白莉娟
陈丽萍,王子丹,赵曙光,白莉娟
(1.东华大学图书馆,上海 201620;2.东华大学信息科学与技术学院,上海 201620;3.华南理工大学自动化科学与信息学院,广州 510640)
基于遗传算法的可逆逻辑综基合于方法及其CUDA并行化实现
陈丽萍1,王子丹2,赵曙光2,白莉娟3
(1.东华大学图书馆,上海 201620;2.东华大学信息科学与技术学院,上海 201620;3.华南理工大学自动化科学与信息学院,广州 510640)
提出和实现了一种基于遗传算法和CUDA(Compute Unified Device Architecture)技术的可逆逻辑并行综合方法.其特点是预先求出并存储可逆逻辑门的组态编码和真值表,通过可逆逻辑门的“定轨级联”构成染色体暨可逆逻辑电路,在迭代中按照预期的逻辑功能和优化目标等部分并行地评估适应度,再利用选择、交叉、变异等部分并行化遗传操作,逐步找到功能正确、性能优化的可逆逻辑电路.实验结果证明了该方法的可行性、有效性,及其与同类传统方法相比在运算速度、求解能力等方面的显著改进.
可逆逻辑电路;综合;可逆逻辑门;遗传算法;GPU并行计算;CUDA
可逆逻辑是研究和实现量子计算(机)、超低功耗集成电路的基础和关键.可逆逻辑综合是根据预期逻辑功能,按照可逆网络无扇出、无反馈等约束条件和限制,利用可逆逻辑门构成相应的可逆逻辑电路并使之尽可能优化,包括门数最少、量子代价最小等.目前研究者已提出多种可逆逻辑电路综合方法.其中一类是先设法生成电路,而后在不改变电路功能的前提下,通过重组、替换等方式对其进行优化.另一类常用方法则将可逆逻辑电路的生成过程与优化过程合二为一,基于遗传算法的可逆逻辑综合方法便属于该类方法[1],且具有灵活、普适等优点,但其较大的算法复杂度限制了其可胜任的电路规模和复杂程度.基于GPU的并行计算架构正是为计算密集型、高强度并行计算而开发,特别适用于基于遗传算法的可逆逻辑综合这类算法复杂度较高且可(部分)表达为并行计算的问题.NVIDIA公司基于其系列GPU和C语言而研发推出的CUDA编程模型[2],为GPU通用计算提供了便捷的开发平台,使得并行化程序的开发难度大大减小.本文研究基于遗传算法的可逆逻辑综合方法及其基于CUDA平台的并行实现,旨在显著提高其运算速度、求解能力,即能够胜任的电路规模和复杂程度.文中给出的进化设计实验结果证明了该方法的可行性、有效性,以及CUDA并行实现所带来的运算速度、求解能力等方面的显著改进.
1 可逆逻辑电路遗传算法模型的建立
1.1 可逆逻辑门的编码
本文不失一般性,以Toffoli门为例来说明可逆逻辑门的编码原理和方法.其他种类的可逆逻辑门的具体编码会有所不同,但编码原理和方法与之类似.
通用Toffoli门是最常用的可逆逻辑门,用TOF(C;t)表示,设输入变量集合为In={x1,x2,…,xn},控制端集合为C={xi1,xi2,…,xik},ik⊂{1,2,…,n},受控端集合t={xj},将输出变量集合映射为:{x1,x2,…,xj-1,xj⊕xi1,xi2,…,xik,xj+1,…,xn}[3-5].
由Toffoli门的性质可知,它只能有一个受控位,但可以有多个控制位和垃圾位.根据控制位、垃圾位的位置和数目的不同,以及受控位位置的不同,Toffoli门有多种不同的组态.对于N位Toffoli门,受控位的位置有CN1种选择,控制位和垃圾位的不同排列一共有2N-1种,故N位Toffoli门的组态总数为CN1×2N-1.
4位Toffoli门的组态总数为C41×24-1=32.为了区分不同的Toffoli门,须为每种Toffoli门组态分配一个不同的编号,32种组态共需要5位二进制数进行编码.但在限定可逆逻辑电路所包含的可逆逻辑门的最大个数的情况下,考虑电路简化等的需要,须允许空门(全线直通)的存在并预留相应的编码.因此,所有的四位Toffoli门加上空门,至少需要C41×24-1+1=33个编号,所以改用6位二进制编码,其中编号000000-011111对应于4位Toffoli门的32种组态,编号100000-111111代表空门.4位Toffoli门编码如图1所示.

图1 4位Toffoli门编码图Fig.1 Code map of 4-bits toffoli gate
1.2 Toffoli门真值表生成
为了评估个体(即可逆逻辑电路)的适应度,需要根据真值表,从外部输入到最终输出,逐个计算其中所含各可逆逻辑门的输出值.为生成某种组态的N位Toffoli门的真值表,须针对其输入组合值0~2N-1,逐个计算其输出值,共计2N次.N位Toffoli门共有CN1×2N-1种组态,所以共需计算CN1×2N-1×2N次.当量子规模较小时,手工完成这些计算还算方便.但随着Toffoli门位数(N)的增加,真值表的规模显著增加,再依靠手工计算既麻烦也容易出错,因此需要编制程序自动生成真值表.其思路是,先找出所有的可逆逻辑门组态,再逐个计算各组态可逆逻辑门的真值表,最后将其写入文件备用.这样可以避免重复计算,提高适应度评估的速度.
对于N位Toffoli门,每根量子线都有3种可能状态:受控位、控制位或垃圾位.受控位的个数只能为1,控制位和垃圾位的个数则为0~N-1.本文对量子线的编码为:0代表受控位,1代表控制位,2代表垃圾位.例如1012代表一个4位Toffoli门,4根量子线依次为控制位、受控位、控制位和垃圾位.据此可寻找所有的Toffoli门组态,并按上述方式编码,具体算法为:先不考虑受控位所在的量子线,将其余的量子线(1或者2)进行全排列,得到控制位与垃圾位的所有组合;再将受控位(0)插入上述组合中的不同位置,即可得到所有的Toffoli门编码.
对于N位Toffoli门,首先不考虑受控位所在量子线,剩下的N-1条量子线都可能为控制位或者垃圾位.对N-1条量子线进行全排列,则有2N-1种排列,其排列算法为:设定N-1个数组,数组长度为2N-1,第1个数组存放的数字为121212…12121212,第2个数组存放11221122…11221122,第3个数组存放11112222…11112222,第k个数组存放(2k-1个1)(2k-1个2)…(2k-1个1)(2k-1个2).然后在每个数组中的相同位置取一个元素,即可得到2N-1个全排列.全排列完毕后,将0依次插入各个量子线之间的可能位置,即可得到所有的N位Toffoli门组态编码.
在此基础上计算Toffoli门各组态的真值表.根据Toffoli门的性质,只有受控位对应的输出是变化的,控制位与垃圾位均为直通.受控位对应的输出值受控制位的影响:若没有控制位,则受控位对应的输出值取反;若有控制位,则受控位对应的输出值等于所有控制位输入值的乘积与受控位输入值的异或,即:当所有控制位输入值的乘积为1时,受控位对应的输出值将取反;当所有控制位输入值的乘积为0时,受控位对应的输出值不变.真值表计算流程如图2所示.
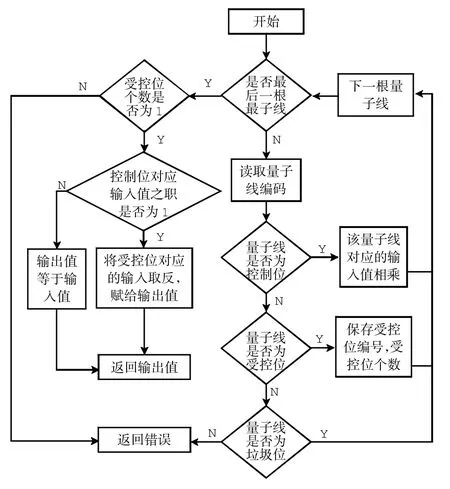
图2 真值表计算流程图Fig.2 Flow chart of truth table calculation
通过上述计算,即可得到所有的Toffoli门组态对应的真值表,并将其写入一个头文件中,使用时在C语言程序中直接包含该头文件即可.同时为便于查看,每算出一种Toffoli门组态的真值表后,都将其Toffoli门编码和对应的真值表写入另一个文件中,一种Toffoli门组态占用其中一行.
1.3 遗传算法模型的建立
1.3.1 基本元素
基因:一个基因代表一个可逆逻辑门,以4位Toffoli门为例,用一个6位二进制数表示一个基因,基因种类共64种.
染色体:一个染色体代表一个可逆逻辑电路,由若干个基因组成.
种群:一个种群代表一个可逆逻辑电路的集合,由若干个染色体组成,在种群中可能包含符合条件的可逆逻辑电路.
适应度:适应度是反应染色体优劣的度量函数.在本文中代表可逆逻辑电路的功能符合度、优化程度的总评分.
1.3.2 适应度评估
以N位可逆逻辑电路为例,染色体的适应度评分规则如下.
规则1:将输入值迭代加载到染色体的各个基因(可逆逻辑门),即每个基因都以其之前(左侧)的基因的输出作为其输入(第一个基因以初始输入值作为其输入),根据相应的真值表求出其输出.最后一个基因的输出为电路的最终输出,若其等于预期输出则适应度增加1.
规则2:若按规则得出的适应度小于2N,说明当前染色体(电路)的最终输出与预期输出不能完全匹配,即可逆逻辑电路的逻辑功能不完全正确,则以该适应度作为最终的染色体适应度.
规则3:在按规则求出的染色体适应度等于2N,即当前染色体(电路)的最终输出与预期输出完全匹配的前提下,按以下方法化简电路并得到最终的染色体适应度.
①若染色体中所含空门的个数为a,则适应度增加a.并且去掉所有空门,继续计算染色体适应度.②若存在相邻且组态相同的可逆逻辑门,则这2个可逆逻辑门可以消去.故可将其等价为2个空门,将适应度增加2,继续计算染色体适应度.③不符合以上2种情况时,以当前适应度作为最终的染色体适应度.评估流程如图3所示.

图3 染色体适应度评估流程Fig.3 Flow chart of chromosome fitness evaluation
2 CUDA并行化实现
2.1 遗传算法的并行化模型
对于计算能力为1.0的显卡,CUDA允许每个线程块中最多开辟512个线程;对于计算能力为2.0的显卡,则允许最多开辟1 024个.当种群中的个体(染色体)过多时,必须启动多个线程块同时运行.鉴于各线程块之间无法进行数据通信,而遗传算法中选择、交叉和变异操作均涉及数据交换,本文将种群分为多个子种群,由线程块完成子种群的进化任务,而后再将子种群中的最优个体迁移到相邻的子种群中去,取代其中的最差个体(只能单方向迁移).对于各子种群,每代的最优个体都与上一代的最优个体相比较,若前者的适应度低于后者,则以后者(即上一代的最优个体)取代前者,从而避免最优个体在进化过程中被淘汰[6].
设种群大小为512×128=65 536,子种群大小为512.相应地在每个线程块中开辟512个线程,共开启128个线程块.每个线程块负责一个子种群的进化任务.进化完成后,由CPU串行代码完成最优染色体的迁移任务.相应的种群结构模型如图4所示.
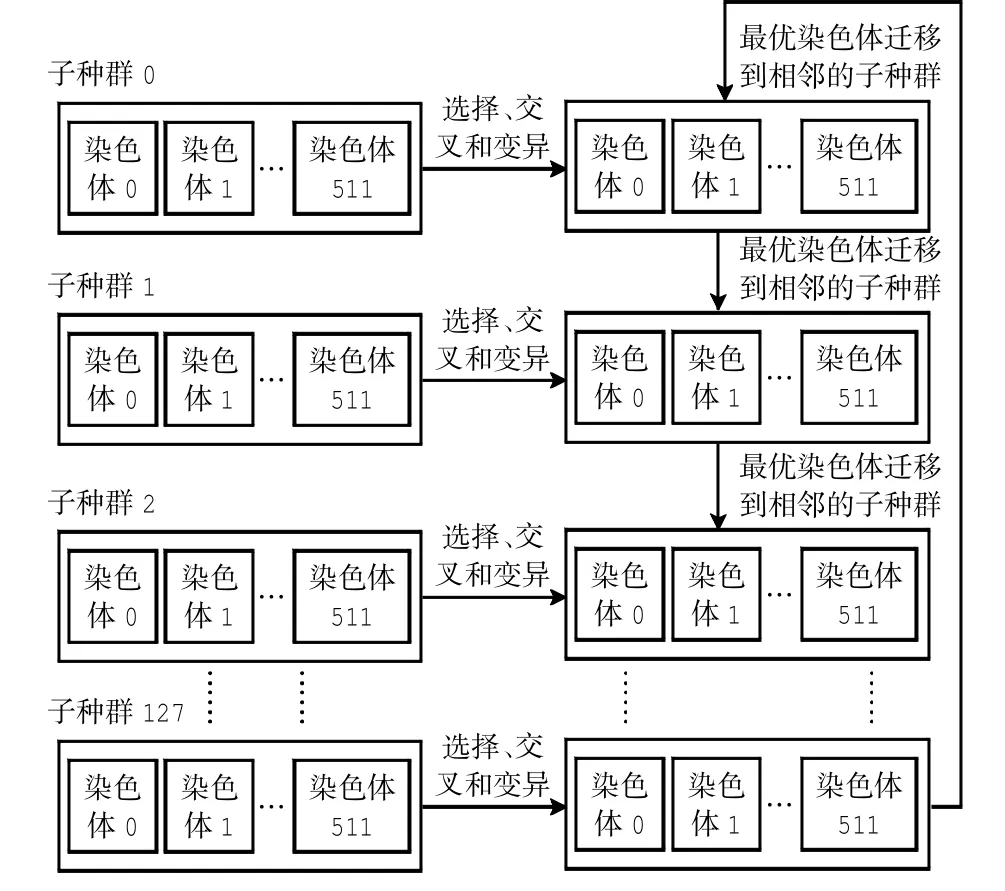
图4 种群结构模型Fig.4 Structure model of population
2.2 遗传算子的并行化实现
2.2.1 并行选择算子
本文选用轮盘赌选择法,其中有2个步骤可以并行化实现,具体操作流程如图5所示.
首先是求适应度的总和,可以利用归约算法并行实现.当子种群规模为512时,其串行实现需要执行511次加法操作,花费时间为511次加法运算的时间总和.若利用并行算法实现,只需9次循环求解即可,因此理论上,其计算速度是串行实现的511/9倍.现举例说明规约求和的具体过程:设c[512]为GPU内的共享内存,保存着每个个体的适应度.按需开启多个线程进行并行计算,第1次开启256个线程,在第n(1≤n≤256)个线程中实现c[n-1]=c[n-1]+c[n-1+256],第1次求和结果存放在c[n-1]中;第2次开启128个线程,在第n(1≤n≤128)个线程中实现c[n-1]= c[n-1]+c[n-1+128],第二次求和结果存放在c[n-1]中;依此类推,第m次开启256/2m-1个线程,在第n(1≤n≤256/2m-1)个线程中实现c[n-1]=c[n-1]+ c[n-1+256/2m-1],第m次求和结果存放在c[n-1]中;最终m=9时开启1个线程,计算c[0]=c[0]+c[1],即得到存放于c[0]中的适应度总和.

图5 并行化选择操作流程图Fig.5 Flow chart of parallel selecting operation
其次是求个体的相对适应度.对于含512个个体的子种群,开启512个线程同时运行,因而仅需一次运算即可得到全体个体的相对适应度.从理论上讲,其计算速度是串行计算的512倍.
2.2.2 并行交叉算子
交叉操作的CUDA并行实现的具体步骤是:首先利用随机数,将子种群中的512个染色体打乱顺序;然后产生随机数并与交叉率Pc相比较,以判断是否需要进行交叉操作.当需要时,在线程块中开启256个线程分别进行交叉操作.让第1个染色体和第256个染色体交叉,第2个染色体和第257个染色体交叉,依此类推,一次即可完成整个种群的交叉操作.理论上,其速度是串行化实现的256倍.具体操作流程如图6.
2.2.3 并行变异算子
变异是对种群中的染色体的某些基因的基因值作变动的操作.本文采用二进制编码和对应的二进制变异.在具体的CUDA并行实现上,利用多个线程同时、分别完成一个个体的变异操作.首先产生随机数并与变异概率Pm做比较,若其值较小则表示某个基因的某一位达到了变异条件,因而立即对该位取反;否则保持不变.对于规模为512的子种群,开启512个线程同时进行上述变异操作.理论上,其执行速度是串行实现的512倍.具体流程如图7所示.
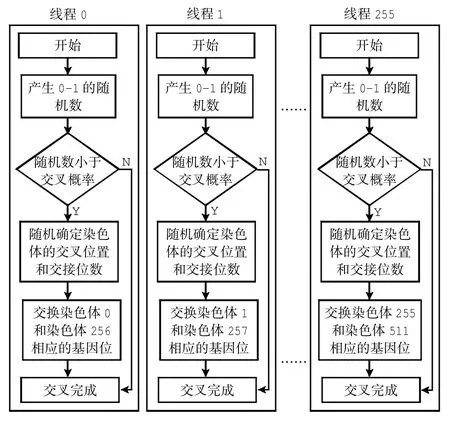
图6 并行化交叉操作流程图Fig.6 Flow chart of parallel cross operation

图7 并行化变异操作流程图Fig.7 Flow chart of parallel mutation operation
3 实验结果及分析
本文利用CUDA C语言,在VS2010平台上编程实现了上述算法,并针对一组可逆逻辑测试基准问题进行了实验.下面给出二个实验结果并稍加分析,其中,种群规模均选定为128×512=65 536,染色体长度均选定为20个基因(即电路中最多包含20个可逆逻辑门).所用显卡为NVIDIA公司的GeForce GT610,其核心频率为810 MHz,显存容量为1 024 MB,显存频率为1 800 MHz,显存带宽为14.4 Gbit/s.
3.1 量子电路4_49设计实验
该电路为四输入四输出,故选用4位Toffoli门,其基因长度为6位,相应的染色体长度为120.预先按照2.3节所述方法,生成4位Toffoli门的真值表及其组态编号.编译并运行程序后,得到的最优染色体为:011101,101100,011111,111101,101011,000011,000 001,011110,000101,000101,111100,010100,001010,011001,101111,000001,100100,011111,010110,001110.对应的十进制数为:29,44,31,61,43,3,1,30,5,5,60,20,10,25,47,1,36,31,22,14.将其中编号32以上的空门消去,化简为29,31,3,1,30,5,5,20,10,25,1,31,22,14.再将其中组态相同且相邻的门消去,化简为29,31,3,1,30,20,10,25,1,31,22,14.根据图1所示的4位Toffoli门编码图,转换得到的可逆逻辑电路如图8所示.

图8 4_49量子电路设计结果Fig.8 4_49 quantum circuit designed
3.2 Decod24-enable设计实验
该电路为六输入六输出,故选用6位Toffoli门,如2.2节所述,6位Toffoli门的受控位位置有C61种变化,控制位和垃圾位的位置共有26-1种变化,故6位Toffoli门的组态总数为C61×26-1=192,其基因长度需选为8,相应的染色体长度为160位(20门).
预先按照2.3节所述方法,生成六位Toffoli门的真值表及其组态编号.编译并运行程序后,得到的最优染色体为:01110101,11000111,00100110,01010110,00000110,00001111,00001111,00010101,01010110,01101011,11010001,00011011,01100110,00011011,00010101,00010101,00110011,01110101,01001011,01101011.对应的十进制数为:117,199,38,86,6,15,15,21,86,107,209,27,102,27,21,21,51,117,75,107.将其中编号192以上的空门消去后,得到117,38,86,6,15,15,21,86,107,27,102,27,21,21,51,117,75,107.再将其中组态相同且相邻的Toffoli门消去,得到117,38,86,6,21,86,107,27,102,27,51,117,75,107.其对应的Toffoli门组态分别为210212,112201,212021,112210,212120,212021,120122,221220,110221,221220,211202,210212,121 022,120122.因为如前所述,0、1、2分别代表受控位、控制位和垃圾位,据此还原各Toffoli门的组态,最终得到的可逆逻辑电路如图9所示.
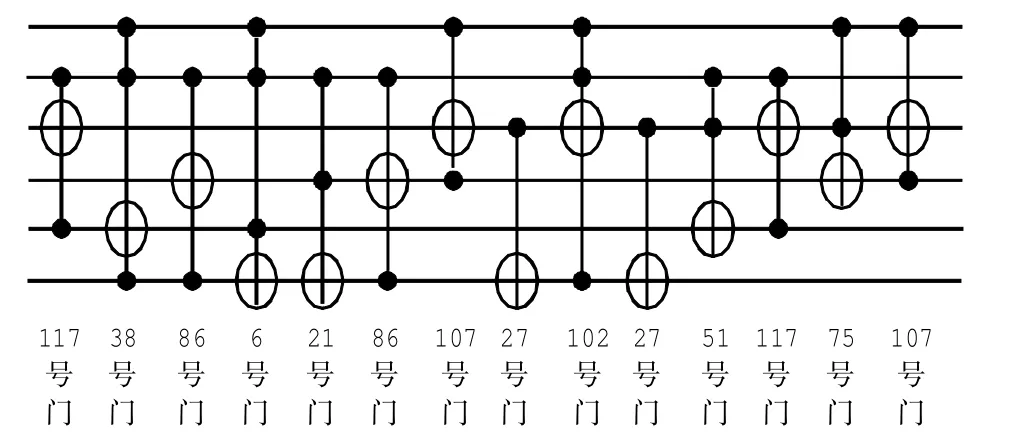
图9 Decod24-enable量子电路设计结果Fig.9 Decod24-enable quantum circuit designed
3.3 CUDA并行实现效率分析
在实验中,针对4位Tottoli门构成电路开发了CPU串行实现程序,该程序完全由C语言实现,仅在CPU上运行,其功能和参数与CUDA并行实现程序完全一致.针对相同的种群规模,分别运行CPU串行程序和CUDA并行程序并记录它们的单次进化任务所用时间,如图10所示.
从图10可以看出,CUDA并行化实现的执行效率大大优于CPU串行实现,且其优势随着种群规模的增大而愈加显著,可以达到上百倍的加速比.因此对于相同的进化次数,CUDA并行实现所花费的时间显著减少,所以有可能完成较大规模、较复杂可逆逻辑电路的进化设计.

图10 CPU串化实现与CUDA并行实现的运行效率对比图Fig.10 Efficiency comparison between CPU realization and CUDA parallel realization
4 结束语
本文研究了一种基于遗传算法的可逆逻辑综合方法,并利用CUDA技术对其进行了并行化改造和编程实现,获得了基于遗传算法和CUDA技术的可逆逻辑并行综合算法和程序.进化设计实验结果表明该算法具有可行性和有效性,且求解的速度和能力均有显著改进.从原理上讲该算法适用于各种可逆逻辑门及其构成的电路,因而具有一定的参考和推广价值.
[1]张舒,褚艳丽.GPU高性能运算之CUDA[M].北京:北京水利水电出版社,2009.
[2] 管致锦.可逆逻辑综合[M].北京:科学出版社,2011.
[3]MASLOV D,DUECK G W,MILLER D M.Toffoli network synthesis with templates[J].IEEE Transactions on CAD,2005,24(6):807-817.
[4]MASLOV D,DUECK G W,MILLER D M.Techiques for the synthesis of reversible Toffoli networks[J].ACM Trans Des Autom Electron Sys,2007,68(12):42-46.
[5]MILLER D M,MASLOV D,DUECK G G.A transformation based algorithm for reversible logic synthesis[C]//Design Autom Conf.2003:318-323.
[6]谭彩凤,马安国,邢座程.基于CUDA平台的遗传算法并行实现研究[J].计算机工程与科学,2009,31(A1):68-72.
Reversible logic synthesis method based on genetic algorithm and its
CUDA parallel implementation CHEN Li-ping1,WANG Zi-dan2,ZHAO Shu-guang2,BAI Li-juan3
(1.Library,Donghua University,Shanghai 201620,China;2.College of Information Science and Technology,Donghua University,Shanghai 201620,China;3.School of Automation Science and Engineering,South China University of Technology,Guangzhou 510640,China)
A parallel synthesis method for reversible logic based on the genetic algorithm and the CUDA technique is discussed.It features the configuration encodings and truth tables prepared and stored in advance for reversible logic gates,chromosomes comprised of encodings of reversible logic gates contained in individuals(reversible logic circuits),partly parallel fitness evaluation according to logic expected logic functions and optimization objectives,and partly parallel genetic operations such as selection,crossover,and mutation.With these steps assembled together and executed iteratively,functionally correct and performance optimal reversible logic circuits can be probably obtained.The experimental results show feasibility and effectiveness of the method proposed,and its advantages over existing non-parallel methods in operation speed and solving ability.
reversible logic circuits;synthesis;reversible logic gates;genetic algorithm;GPU parallel computing;CUDA
TP312.8;TP331.1
A
1671-024X(2014)03-0069-06
2013-12-2
国家自然科学基金面上项目(61271114);上海市教委科研创新重点项目(14ZZ068)
陈丽萍(1965—),女,硕士,工程师.
赵曙光(1965—),男,教授.E-mail:sgzhao@dhu.edu.cn
