基于滑模变结构的感应电机效率优化技术
2014-03-15崔春艳苗敬利
崔春艳,李 奎,李 兵,苗敬利,付 超
(1.河北工业大学电磁场与电器可靠性省部共建重点实验室,天津 300130;2.河北工程大学信息与电气工程学院,河北 邯郸 056038)
基于滑模变结构的感应电机效率优化技术
崔春艳1,2,李 奎1,李 兵2,苗敬利2,付 超1
(1.河北工业大学电磁场与电器可靠性省部共建重点实验室,天津 300130;2.河北工程大学信息与电气工程学院,河北 邯郸 056038)
针对常用的电机矢量控制系统中不考虑铁损的问题,为优化电机运行效率,提出一种基于滑模变结构的感应电机效率优化控制技术.在感应电机两相静止坐标系中建立了并联电阻型电机损耗模型;设计了基于二阶滑模的控制器,并利用超螺旋控制算法解决了相关度为1的滑模控制中抖动问题;利用李亚普诺夫稳定定理,证明了该控制系统的稳定性,同时推导出相应控制器的增益参数.Matlab Simulink仿真结果表明:基于滑模的效率优化控制方法不仅能够降低电机损耗,提高电机运行效率,而且具有很好的动态调速性能,抗干扰性好,鲁棒性强.
滑模变结构;铁损模型;效率优化;感应电机
为了解决矢量控制系统中的感应电机轻载低效问题,国内外许多学者提出了多种效率优化控制方法,根据优化原理可以分为基于最小输入功率控制和基于损耗模型控制二大类[1].最小输入功率控制的原理是在输出功率不变的前提下使输入功率最小.它的优点是不依赖于数学模型,缺点是要求输入功率的检测精度高并且在线搜索时间长,因此不适用负载变化快的调速系统.基于损耗模型的效率优化技术是基于建立的异步电机损耗模型,利用数学中函数求极值的方法,求出电机损耗最小时对应的最优磁链.该技术早期文献[2-4]说明了通过选择最优磁链来降低损耗的可能性,在标量和矢量控制系统中,分别建立了数学模型,求出了最优磁链方程.文献[5]在两相旋转坐标系中,建立了电机考虑铁损的损耗模型,提出了一种矢量控制变频调速的效率优化控制方法,解决了动态响应速度慢的问题.文献[6]进一步讨论了铁损变化时,对矢量控制的异步电机效率优化控制的影响,并给出了在动态和稳态的2种补偿方法,以减弱铁损电阻变化的影响.文献[7]将遗传算法应用于感应电机的效率优化控制,保证电机在输出功率不变的情况下,使电机始终运行在最小损耗状态.文献[8]利用观测器在线辨识感应电机模型参数,以避免对损耗模型参数波动的影响.文献[9]分析了电机损耗与转矩、转速和定子磁链之间的关系,给出了电机稳态运行时效率最优的定子磁链幅值计算公式,实现了感应电机无差拍直接转矩控制变频调速系统的效率最优控制.文献[10]通过分析电机损耗与转矩、转速和定子磁链的关系,导出了不同运行工况条件下效率最优的定子磁链幅值计算式,实现了感应电机直接转矩控制变频调速系统的效率最优控制.文献[11]通过电机损耗模型选取最优励磁电流搜索初值,采用自寻优方法在已经缩小的范围内搜索系统的最大效率运行点.文献 [12]通过研究定子电流和电机损耗的关系,提出了基于电机损耗模型的效率优化方案.文献 [13]通过研究转子铁损耗在整个铁损耗中所占比例和同步角频率的关系,利用拉格朗日优化算法,推导出感应电机在矢量控制下稳态运行时效率最高的控制条件.本文通过分析基于损耗模型的感应电机效率优化的研究现状,可知基于损耗模型的效率优化方法主要存在如下两个问题:一是当前研究的感应电机损耗模型均是基于旋转坐标系建立的.由于在旋转坐标系中,转子速度和磁链是解耦的,因此认为输出转矩与励磁电流有关,进而简化控制.但是这种解耦结论的前提条件是假设转子磁链已经达到稳态值[14].二是这种效率优化控制方法需要建立一个可靠正确的损耗模型,对模型参数的依赖性强[15].因此为了提高基于损耗模型的电机效率优化性能,本文基于两相静止坐标系下的电机损耗模型,运用滑模变结构控制技术,避免了磁链稳定的假设,提高了系统的鲁棒性.最后利用李亚普诺夫稳定定理证明了滑模控制器的稳定性.
1 考虑铁损的感应电机模型
考虑铁损时,感应电机在两相同步静止坐标系下等效电路图如图1所示.
根据等效电路图,利用结点电流法和回路电压法,可以列出方程(1).
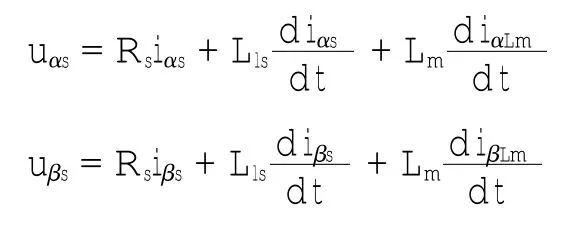
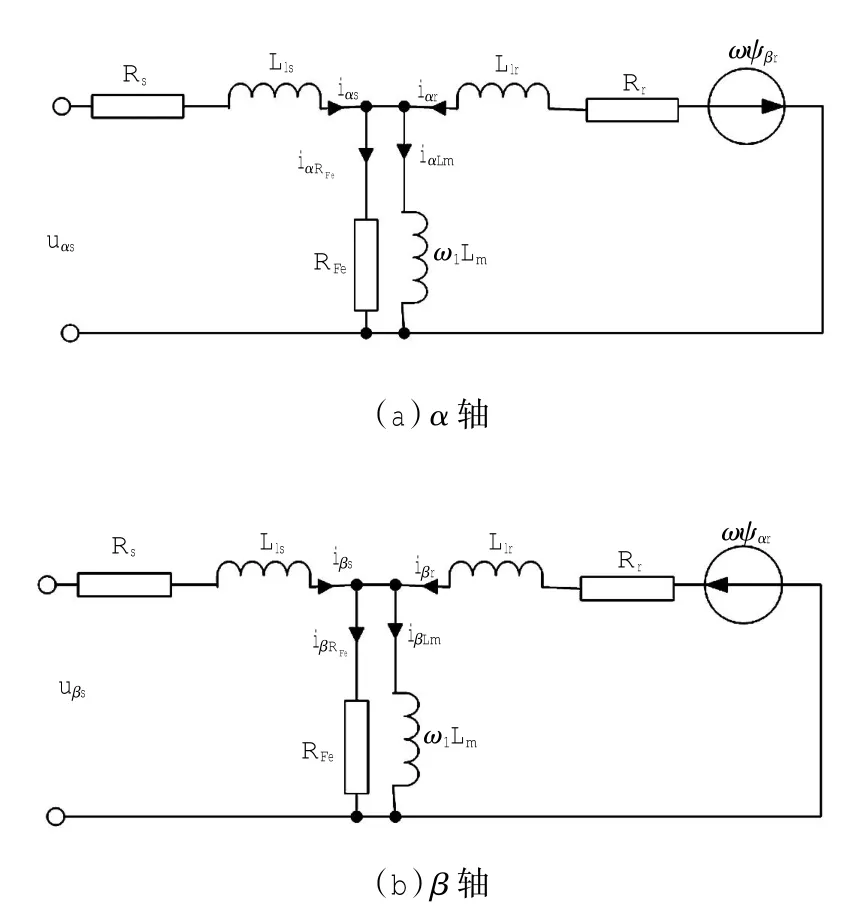
图1 两相静止坐标系下感应电机等效电路Fig.1 IM equivalent circuit in two phase stationary frame

在静止参考坐标系中转子磁链可由转子电流和励磁电流表示为式(2).

由于转子电感Lr是转子漏感Llr和互感Lm之和,即Lr=Llr+Lm,所以由式(2)可以得到转子电流的表达式为式(3).

由于考虑铁损时的机械方程和不考虑铁损时一样,同时为了后面推导滑模控制器书写方便,根据方程式(1)、(2)、(3)将考虑铁损的三相异步感应电机在两相静止参考坐标系中的数学模型整理如下:
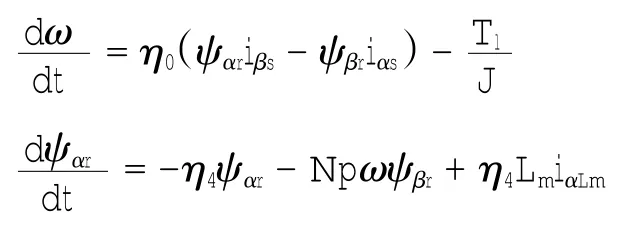
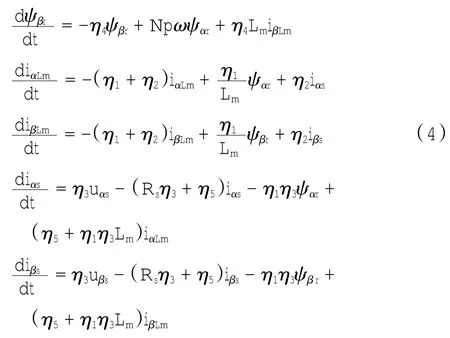
式(4)中引入的各个η参数,是为了后续推导时方便,各参数和原有参数的关系分别如下:
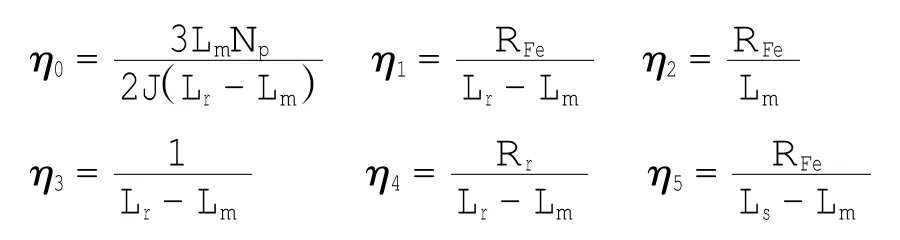
式中:ω为转子角速度;uαs、uβs均为定子电压;iαs、iβs均为定子电流;iαLm、iβLm均代表励磁电流;ψαr、ψβr均为转子磁链;Tl为负载转矩;Np为极对数;J为转动惯量;Lr、Ls、Lm、Llr和Lls分别为转子电感、定子电感、励磁电感、转子漏感和定子漏感;Rr、Rs和RFe分别为转子电阻、定子电组和铁心电阻.
2 最优磁链计算
由电机的效率方程(5)可知,要想提高电机效率,可通过降低电机损耗功率来获得,即保证输出功率不变的前提下,通过降低损耗功率来实现,目前的感应电机效率优化控制基本上均是基于这个思路来实现.而电机损耗中的可控损耗部分与电机相应的转定子电阻和电流有关,可由方程式(6)表示.
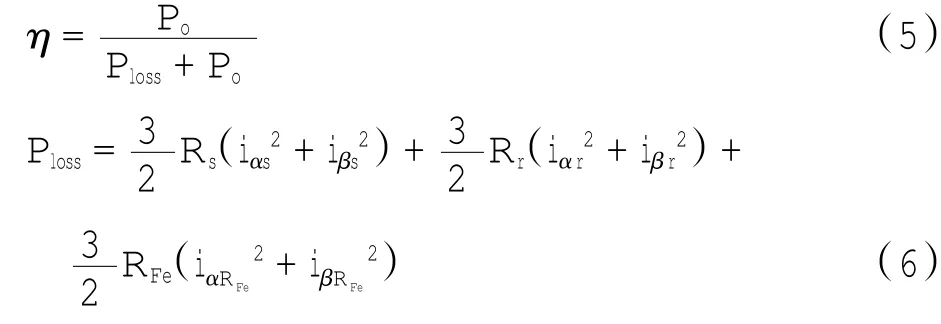
式中:iαRFe、iβRFe均代表通过铁芯的电流.由式(6)可以看出,电机损耗Ploss方程是一个正定函数,所以一个会存在一个期望的转子磁链使损耗极小.引入一个转子磁链矢量ψr=(ψαrψβr),用ψro=(ψαoψβo)代表最优转子磁链矢量.利用函数求极值的方法,电机损耗函数求导数,并令导数为零时,可以求出对应损耗极小时对应的转子磁疗,即最优磁链.
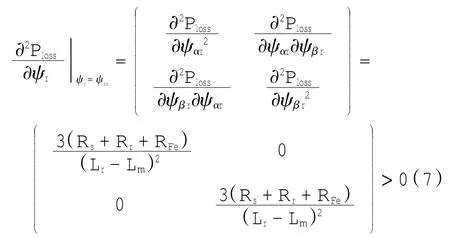
由方程式(7)可知,Hessian矩阵在极小值处是正定的,因此令方程式(6)的一阶导数为零,即可推导出最优磁链的表达式(8).

3 考虑铁损的超螺旋滑模控制器设计
由于滑模变结构控制技术对于系统参数的依赖性低,呈现出较强的鲁棒性,因此近年来在解决不确定非线性系统的控制问题上得到了广泛应用,但是当前的研究主要集中在滑模观测器和滑模控制器方面,在感应电机效率优化方面的文献报道较少.本文根据电机损耗数学模型,采用滑模变结构控制器,克服了损耗模型对参数的依赖性强的问题,同时利用超螺旋控制律减弱滑模控制方法中的抖动现象.
3.1 控制器设计
电机控制的主要目的不仅是效率优化,还要保证转子角速度和转子磁链能够分别跟随设计值变化.因此,设动态跟踪的误差信号为z1=ω-ωr和z2=ψmψmr.考虑到效率最优的问题,这里ψmr=ψαo2+ψβo2,当动态跟踪的误差信号为0时,则从动态调速和效率优化2个方面保证控制系统的性能.由方程式(4)的第1、第2和第3个式子,可以得到误差的动态表达式(9).
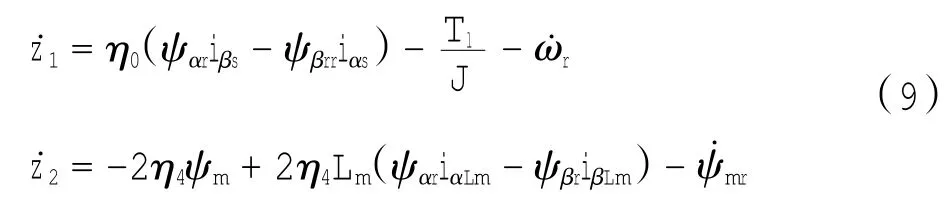
式(9)中2个方程对于输出z1和z2相对阶分别为2和3,因此这里用传统的滑模控制无法实现.将z2的动态方程改写为z˙2=k2z2+z3(其中k2为<0的常数),所以新变量z3可以表示为:

利用上述的z1和z3定义一个新的矢量ζ1=(ζ1,1,ζ2,1)T=(z1,z3)T,因此结合方程式(4)可得:
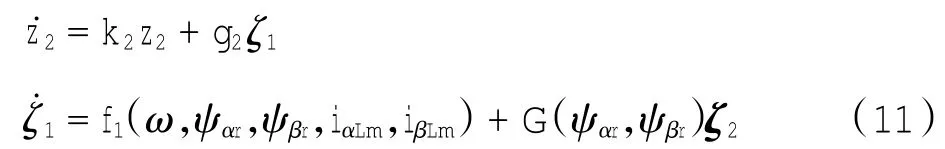
式(11)中新增加的变量和函数分别为:

为了保证式(11)的稳定性,构造一个Hurwitz矩阵K1,并假设矢量ζ1的动态方程式为式(12).
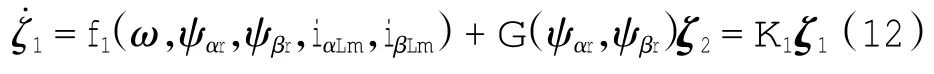
由式(12)可知,由于矩阵G的行列式det(G)=-2η0η2η4Lmψm,因此只要假设ψm≠0,则G-1存在.因此可以从式(12)中计算出定子电流矢量的参考值ζ2*= G-1(·)(K1ζ1-f1(·)),其中ζ2*=(iαs*,iβs*),所以只要通过电机定子的电流能够跟随上述参考值,则动态跟踪的误差信号z1和z2将渐近衰减为0.因此为了使得定子实际电流能够跟踪参考电流,定义定子电流误差矢量ζ3=(ζ3,1,ζ3,2)T=ζ2-ζ2*.定子电流的误差矢量的动态方程,可以由式(13)导出.

式中新增加的函数和变量分别为:
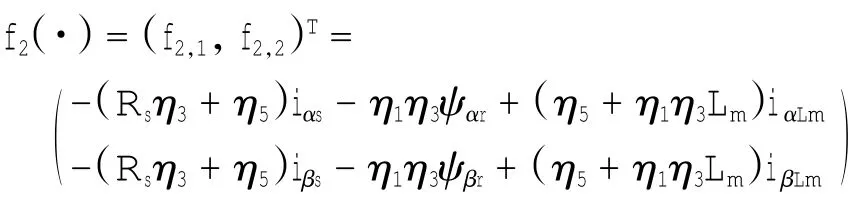
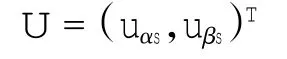
因此,将ζ3,1和ζ3,2看做滑模函数.由于超螺旋控制算法仅仅需要滑模量的信息,不需要知道其导数的信息就可以解决相关度为1的滑模控制中抖动问题,因此构造uαs,uβs的超螺旋滑模控制器,控制律如式(14)所示.
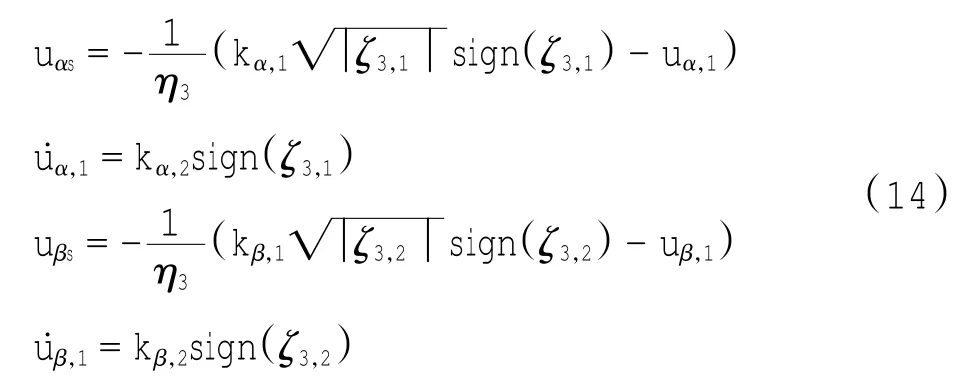
式中:kα,1、kα,2、kβ,1和kβ,2为控制器的增益参数,它们通过下面的稳定性分析来确定.
由式(11)中f12(·)的方程式可知,mr和mr与输入信号和输入信号的导数有关,这里采用鲁棒性强的精确微分器来计算,微分器结构如下.
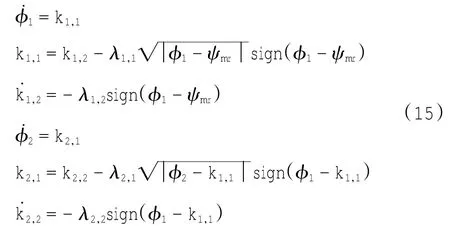
式中:λ1,1,λ1,2,λ2,1,λ2,2>0,输入信号微分后为ψmr,
3.2 控制器稳定性分析
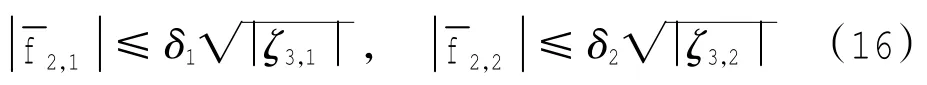
式中:δ1>0;δ2>0.
由方程式(13)的最后一个式子,并结合式(14)的超螺旋控制律,可以得到式(17).
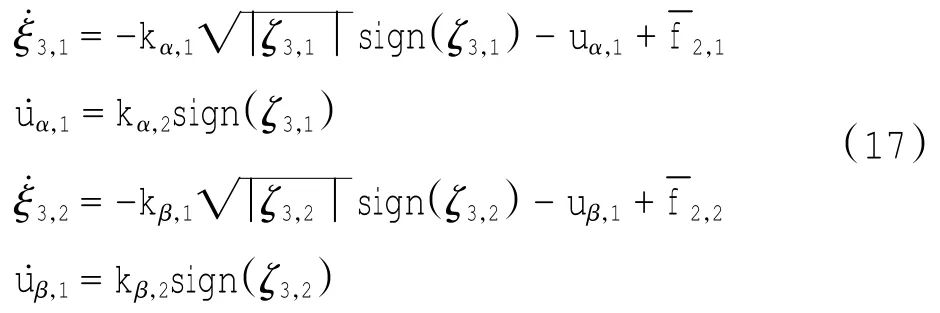
根据李亚普诺夫稳定,定义李亚普诺夫函数为


式中新引入的矢量分别为:
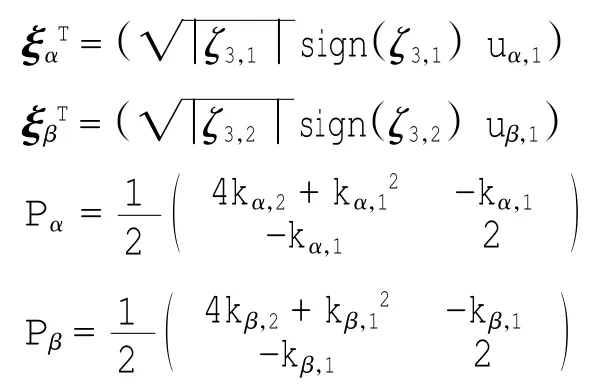
对式(18)求微分,来证明李亚普诺夫函数是负定的.证明过程如下:

在式(19)中考虑式(16)限定的扰动信号的边界,则式(19)可以简化为:
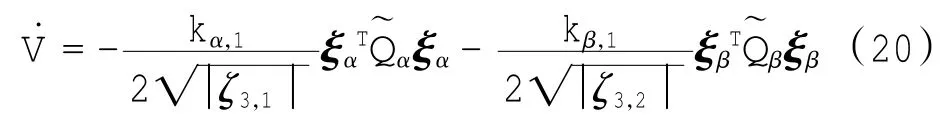
式中新引入的矢量为:
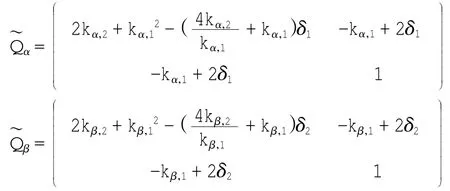
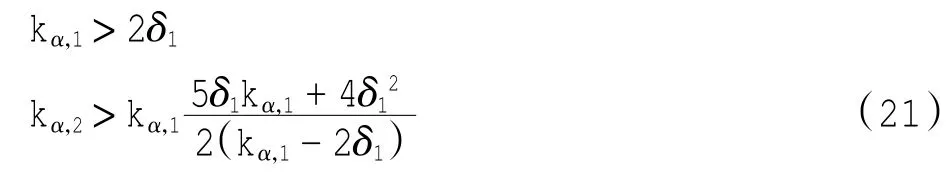

4 Matlab仿真分析
本文利用Matlab仿真软件,对考虑铁损的异步电机感应电机进行效率优化的控制技术进行仿真,仿真用感应电机参数及系统中用到的控制增益参数参如表1所示.
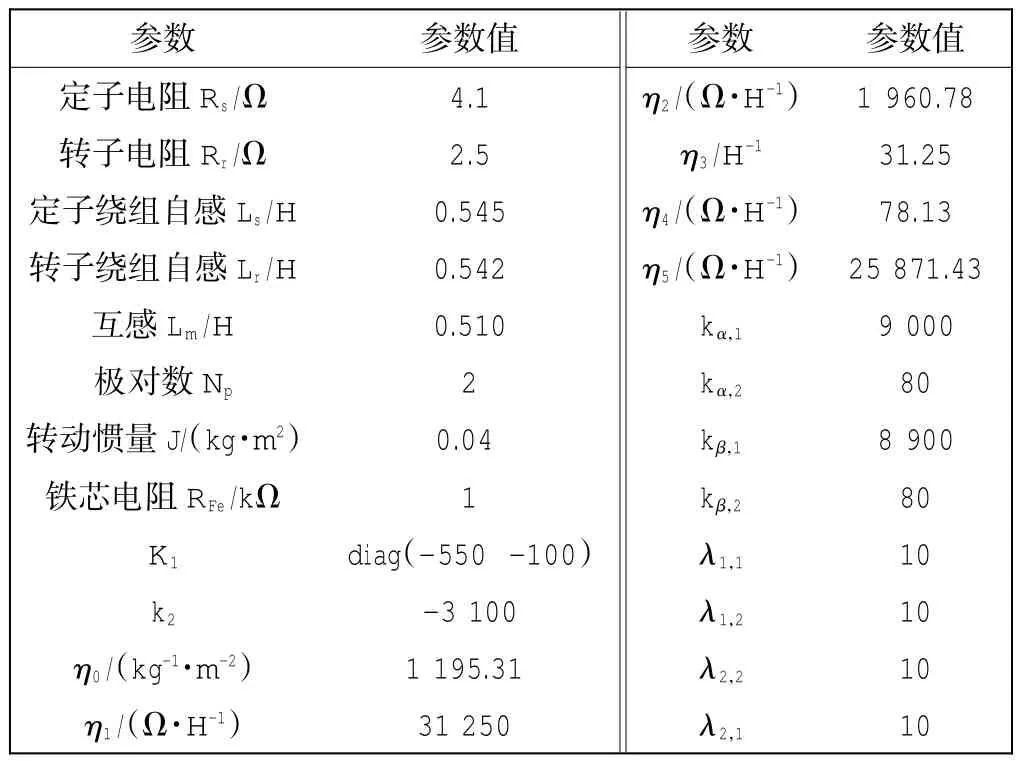
表1 电机参数和控制器增益参数Tab.1 Motor parameters and gain parameters of controller
仿真用负载转矩如图2所示.
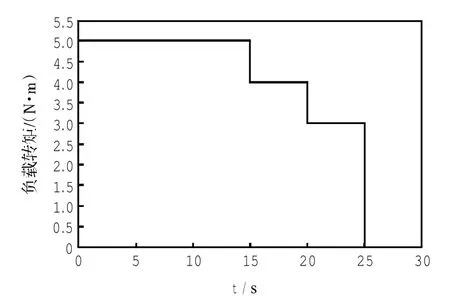
图2 负载转矩Fig.2 Load torque
在0~15 s内,负载转矩为5 N·m;在第15 s,减少1 N·m,变为4 N·m;然后一直保持到第20 s,又继续减少1 N·m,变为3 N·m;接着一直保持到第25 s,然后负载转矩变为0.转子参考速度在前10 s,一直从0增加到190 rad/s,然后一直保持不变.
在开环控制时,考虑和不考虑铁损时转子的跟随特性以及磁链幅值的平方,如图3和4所示.
由图3可以看出,对于同样的参考速度,稳态的转子速度是相同的,但是瞬态响应特性不同.考虑铁芯电阻时的响应时间比不考虑时要快.这是由于在按照指数快速增加的励磁电流导致定子启动电流迅速增加,因此使得响应速度变快.由图4可知,获得的转子磁链幅值的平方分别为1.6 Wb2和0.16 Wb2,这也和当前各种文献中的磁链参考值相符合,而且显然考虑铁芯时的磁链建立速度快,这也进一步说明了考虑铁损时的转子速度瞬态响应时间快的原因.

图3 开环控制时的转子速度比较Fig.3 Comparison of rotor velocity for open loop control
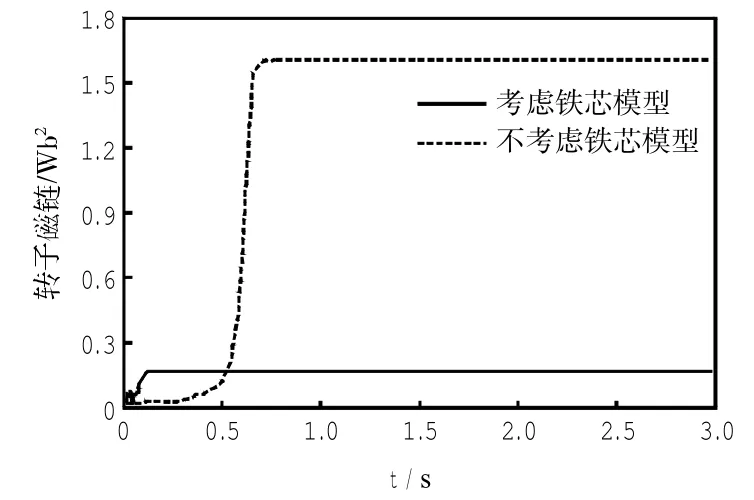
图4 开环控制时转子磁链比较Fig.4 Comparison of rotor flux for open loop control
在闭环控制时,无论是否考虑铁芯,转子速度均具有很好的跟随特性.但是在闭环控制时,计算的最优磁链却不同,具体的轨迹曲线如图5所示.

图5 闭环控制时最优转子磁链比较Fig.5 Comparison of optimal rotor flux for close loop control
从图5可以看出,考虑铁芯时,计算出的最优磁链值低于不考虑铁损时的值,而且考虑铁损时的最优磁链的变化趋势类似于负载转矩的变化.如图2中负载转矩分别在第15 s、第20 s和第25 s时减少,而图5中的转子磁链也是分别在第15 s、第20 s和第25 s时减少.同时由于不考虑铁损时的最优转子磁链大,这就意味着这些超出的额外磁链将使得电机电流增加,这也就必然意味着电机损耗的增加,从而降低了电机效率.在这2种情况下,电机的损耗如图6所示.
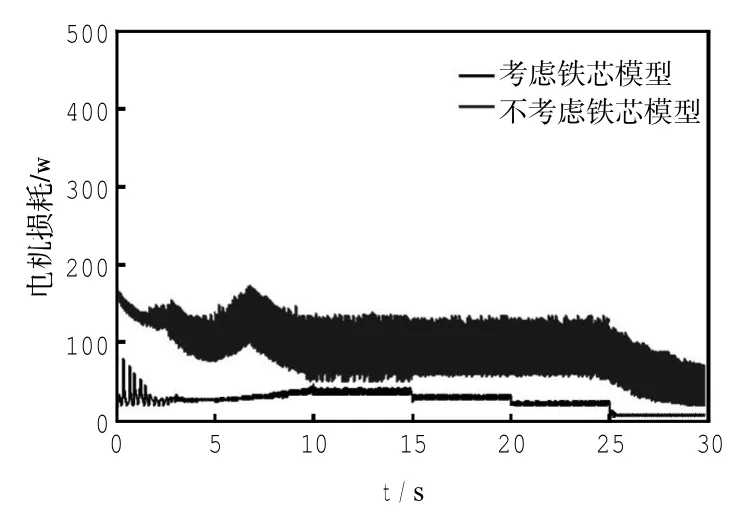
图6 电机损耗比较Fig.6 Comparison of power loss
由于电机参数随着温度升高,并不是恒定的,特别是定子电阻和转子电阻.因此最后讨论参数变化时,所引起转子速度和最优磁链波动的情况.ΔRs和ΔRr分别表示定子电阻和转子电阻变化的百分比;Δωr和Δψmr分别表示转子速度和最优磁链波动的百分比(设稳态时最优磁链为0.047 Wb2).
参数扰动下的电机性能如表2所示.
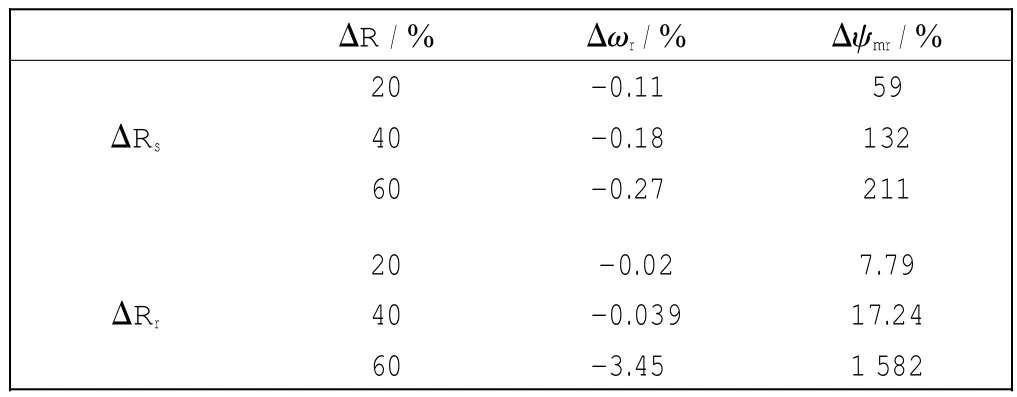
表2 参数扰动下的电机性能Tab.2 Motor performance under parameters variation
从表2可以看出,转子速度的抗扰性能比较好,但是最优磁链随着电机参数的波动变化比较大.但是如果和开环控制时相比较,采用这种算法的抗扰性仍然提高很多.开环控制时,通常假设磁链参考值为1.6 Wb2,则变化百分比为
5 结束语
本文在两相静止坐标系中,基于并联电阻三相异步感应电机等效电路图,建立了含有铁损的感应电机数学模型,计算了基于损耗最小的最优磁链.由于普通滑模的高频抖动问题,因此文中设计了采用超螺旋算法的二阶滑模控制器,以削弱滑模控制中的抖动.利用李亚普诺夫稳定定理证明了控制系统的稳定性,通过Matlab Simulink仿真显示了上述考虑铁损的感应电机效率优化控制方案,不仅能够具有很好的调速性能,并且能够降低电机损耗,提高电机运行效率,且控制系统抗干扰性好,鲁棒性强.
[1] 林显军,程小华,龙洪宇.异步电动机效率优化控制策略综述[J].微电机,2011,44(7):81-84.
[2]LORENZ R D,YANG S M.Efficieney optimized flux trajectories for closed cycle operation of field orientation induetion maehinedrives[J].IEEE Transactions on Industry Applications,1992,28(3):574-58.
[3]GARCIA G O,LUIS J C M,STEPHAN R M.An efficient controller for an adjustable speed Induction motor drive[J].IEEE Transactions on Industrial Electronics,1994,4(5):533-539.
[4]KIOSKERIDIS I,MARGARIS N.Loss minimization in induction motor adjustable speed drives[J].IEEE Transactions on Industrial Electronics,1996,43(l):226-231.
[5] 崔纳新,张承慧,孙丰涛.异步电动机的效率优化快速响应控制研究[J].中国电机工程学报,2005,25(11):118-123.
[6] 李坷,张承慧,崔纳新.考虑铁损的电动汽车用感应电机矢量控制及其能量优化策略[J].控制理论与应用,2007,24(6):959-968.
[7] 马秀娟,刘金凤,李宏宇,等.基于遗传算法的感应电机效率优化控制研究[J].微电机,2013,46(10):36-40.
[8] 刘艳,徐春.电动汽车电机驱动系统效率优化控制研究[J].微电机,2013,46(3):46-49.
[9] 聂晶,张兴华,孙振兴.效率最优的感应电机无差拍直接转矩控制[J].电气传动,2013,43(10):23-27.
[10]张兴华,孙振兴,王德明.电动汽车用感应电机直接转矩控制系统的效率最优控制[J].电工技术学报,2013,28(4):255-260.
[11]李子昀.一种考虑铁耗的感应电机最大效率控制系统[J].大电机技术,2011(3):17-20.
[12]金梅,侯楚林.基于损耗模型的感应电机效率优化控制研究[J].电测与仪表,2011,47(12):27-30.
[13]徐占国,邵诚.感应电机最大效率控制时损耗模型研究[J].大连理工大学学报,2010(5):762-766.
[14]阮毅,陈伯时.电力拖动自动控制系统-运动控制系统[M].北京:机械工业出版社,2010:179-189.
[15]崔纳新,张承慧,杜春水.变频调速异步电动机效率优化控制的研究[J].电工技术学报,2004,19(5):36-42.
Efficiency optimization of induction motor technology based on sliding mode variable structure
CUI Chun-yan1,2,LI Kui1,LI Bing2,MIAO Jing-li2,FU Chao1
(1.Province-Ministry Joint Key Lab of Electromagnetic Field and Electrical Apparatus Reliability,Hebei University of Technology,Tianjin 300130,China;2.School of Informantion and Electric Engineering,Hebei University of Engineering,Handan 056038,China)
For the optimization of motor efficiency,a kind of control efficiency optimization of induction motor based on sliding mode variable structure is presented to solve the problem without considering the iron loss of motor vector control system.The parallel resistance motor loss model in the two-phase stationary coordinate is set up.The controller is designed based on the two order sliding mode,and solves the problem of chattering of sliding mode control for the correlation degree 1 by the super twisting algorithm.The stability of the control system is proved by Lyapunov stability theorem,and the gain parameter of controller is deduced.Matlab Simulink simulation shows that the efficiency optimization control method based on the sliding mode can reduce the motor loss,improve the operating efficiency of the motor,has good dynamic speed performance and good anti-interference performance and strong robustness.
sliding mode variable structure;iron loss model;efficiency optimization;induction motor
TM346.2
A
1671-024X(2014)03-0059-07
2013-12-31
国家自然科学基金项目(11272112);河北省科技支撑项目(12213912D)
崔春艳(1976—),女,博士研究生,讲师.E-mail:swallow_ccy@163.com
