HTPB/IPDI弹性体的粘-超弹性本构模型研究①

胡少青，鞠玉涛，韦 震，周长省

(南京理工大学 机械工程学院，南京 210094)

0 引言

HTPB弹性体是端羟基聚丁二烯与环氧类、有机二元酸或二异氰酸酯等固化剂反应生成的一种聚氨酯，以其良好的力学及工艺性能，广泛用于复合推进剂的粘合剂，固体推进剂耐烧蚀包覆材料[1]等。此外，还用于隔振材料、密封材料等方面。掌握其力学性能及本构模型是深入研究和应用这类复合材料的基础。

近年来，一些学者对聚氨酯材料的本构模型有了一定的研究。Shu L H[2]及刘柏峰等[3]在研究聚氨酯隔振器的静态力学响应时，忽略了聚氨酯材料的粘性特征，将其假设为超弹性材料，用含应变能的超弹性模型来表示材料的力学特性，但该模型不能适应动态状况下聚氨酯材料的力学性能的描述。Yang L M[4-7]等相继提出的适应于橡胶材料的粘-超弹本构模型，这类本构模型多用于描述材料在高应变率下的动态力学性能；Pawlikowski M[8]成功地将粘-超弹本构模型成功的应用于聚氨酯纳米复合的研究中。HTPB弹性体是较为常用的聚氨酯材料，在低应变率下不仅具有超弹性，而且其粘弹性特征也较显著。目前，关于HTPB弹性体静态及准静态下的粘-超弹本构模型研究较少。因此，本文开展了HTPB弹性体在静态及准静态下的粘-超弹性本构模型的研究，以期为这类材料设计及研究提供依据。

1 HTPB弹性体粘-超弹性本构模型建立

HTPB弹性体属于橡胶类材料，在建立这类材料粘-超弹本构模型时常用超弹性模型与粘弹性模型组合的方法。因此，合理选择粘弹性和超弹性模型及建立准确的模型参数求解方法，是保证模型准确性的关键。

1.1 超弹性本构模型

聚氨酯弹性体同其他橡胶类材料一样可认为不可压材料。常用的超弹模型有Neo-Hookean模型、Mooney-Rivlin模型、Yeoh模型、Ogden模型等。Yeoh模型的剪切模量是随应变的变化而变化，简单变形可用于预测其他变形形式的力学性能，模型适应较宽泛的变形范围，同时模型只考虑不变量I1对应变能函数的影响[9]，形式简单，有利于有限元的应用。因此，本文的超弹性本构模型选用Yeoh模型。

在单轴加载下，设加载方向上的伸长比为λ，由于材料不可压，故三向主伸长比为λ1=λ，λ2=λ3=λ-1/2。则变形梯度张量F及左Cauchy应变张量为

(1)

B的第一不变量：

I1=tr(B)=λ2+2λ-1

(2)

因此，在单轴加载条件下，HTPB弹性体超弹性特征本文采用式(3)，基于Yeoh应变能函数的不可压各向同性弹性固体的超弹性本构模型表达[9]:

(3)

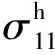
1.2 粘弹性本构模型

粘弹性材料的显著特点是应力应变的率相关性与加载历史相关性，对于各向同性不可压材料的粘弹性本构可表示为[3-4]

(4)

式中σv为Cauchy应力张量；pv为不可压作为一种约束产生的静水压力；C为右Cauchy变形张量C=FT·F；Ω为描述应变历史对应力影响的张量泛函，是坐标系无关量，可写为

(5)

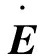
(6)

式中θi为松弛时间；N为Prony级数的阶数，N越大，模型就越逼近真实的材料特性。

松弛时间与微观结构相关，一个试验中的材料松弛时间取决于加载时间与加载速率。Yang L M认为，上述粘弹性模型中的一个松弛时间可准确描述2个数量级的应变率[4]。对于HTPB弹性体，在静态及准静态下主要表现为超弹性，粘弹性对其力学性能影响较一般粘弹性材料小。若直接像一般粘弹性本构中取N=6～10，则会造成模型的复杂程度增加，不利于模型的拟合，也不利于工程数值仿真的应用，且对于模型精度的提高并不显著。为了简化模型，本文在构建HTPB弹性体粘弹性本构模型时，取N=1。

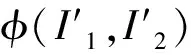
(7)

由式(5)～(7)，不考虑加载前的效应，可得

(8)

则HTPB弹性体粘弹性特征可用式(9)表达：

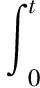
(9)

1.3 粘-超弹性本构模型的建立

在建立HTPB弹性体粘-超弹性本构模型时，同样认为材料由超弹性单元和粘弹性单元并联组合而成，故其总的应力：

σ=σh+σv

(10)

轴向应力：

(11)

将式(3)、式(9)代入式(11)，得一维状况下的HTPB粘-超弹本构模型：

σ11=2(λ2-λ-1)[C10+2C20(I1-3)+3C30(I1-3)2]-

(12)

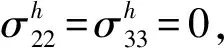
(13)

代入式(12)，可得

σ11= 2(λ2-λ-1)[C10+2C20(I1-3)+3C30(I1-3)2]+

(14)

σ11为Cauchy(真实)应力，单轴加载情况下：

σ11=λP11

(15)

式中P11为工程应力；λ=1+ε11，ε11为加载方向上工程应变。

在单轴拉伸时，本构的两部分均有响应，理论上可用拉伸曲线拟合全部参数。但本构中参数较多，数学方程复杂，可能会出现多解状况，而造成参数或模型失去物理意义。由于这一本构模型在松弛试验应变保持阶段，模型中的超弹部分应力不变，松弛特性只与粘弹部分有关。所以，可用松弛实验结果拟合模型中的与粘弹特性相关的参数A1、A2、θ，再利用单轴等速拉伸实验结果拟合模型中与超弹特性相关的参数C10、C20、C30。这样，可保证模型参数获取的精度及物理意义。

2 材料制备及实验方法

HTPB的弹性体的配方及工艺过程对材料的力学性能影响较大。本文采用的配方为：工业级HTPB、分析纯异弗尔酮二异氰酸酯(IPDI)；固化参数R(—OCH/—OH)=1.05。固化工艺为：准确称量后，先将IPDI和HTPB加入烧瓶中预混，再放入(40±1)℃的恒温水浴中真空状况下搅拌30 min，然后浇注到预先涂硅橡胶及二甲基硅油为脱模剂的模具中，模具尺寸为100 mm×20 mm×8 mm，放入70 ℃干燥保温箱中，保持真空度0.1 MPa，固化168 h。

HTPB/IPDI弹性体较软，直接进行夹持实验，会造成试件两端产生较大的挤压变形，影响实验结果。松弛实验中，在应变保持阶段，试件两端会发生一定的流动，导致“伪松弛现象”，即实验测得应力松弛有一部分是由于流动引起的应变减小导致的，同时使松弛时间增大。这种流动在试验中很难避免，只能改善实验方法减小流动。增加试件的长度可以有效减小流动的影响。改善夹持方法也可提高实验的准确性，本文采用木板框架的粘接夹持方法，如图1所示。

图1 试件示意图及胶片实物图

HTPB弹性体由A、B两种板材组合粘接夹持，试验机夹具夹持A面及相对面，B板可起到支撑作用，防止试件在加持力的作用下，产生较大变形。

采用微机控制电子万能材料试验机在室温30 ℃、湿度34%的环境下，以12.5、25、100 mm/min的拉伸速率，分别对试件进行单轴等速拉伸实验；在拉伸速率为100 mm/min的速率下，拉伸到应变为1时，应变保持600 s，得到材料的松弛特性。实验结果为5个试件的平均值。

3 试验结果及分析

3.1 松弛实验结果分析

理想的松弛实验要求在t=0时给试件加载阶跃应变，但实际试验中，瞬间达到ε0是不可能的，如图2所示。

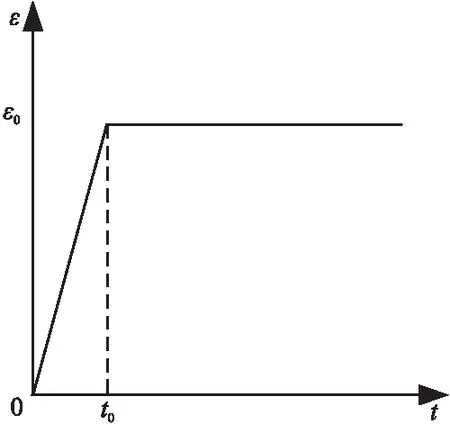
图2 松弛试验应变实际加载过程

实际加载过程数学模型：

(16)

对于模量较大粘弹性材料，在松弛试验中，由于实验加载上升段的时间t0很小，因而可忽略加载段对松弛试验结果的影响，而假设t0=0，对于HTPB材料而言，其模量较低，粘弹性特征在低应变率下没有典型粘弹性材料显著，减小松弛试验的ε0，可减小t0的影响，但会使试验中松弛响应测量结果误差较大。增大ε0，势必造成t0的增大，使加载段影响松弛结果，而不能用松弛函数直接拟合。为了解决实际加载过程中加载段对松弛模量引起的误差。本文利用所提出的本构方程，可求得材料在上述加载条件下的应力响应，进而将这一影响消除。

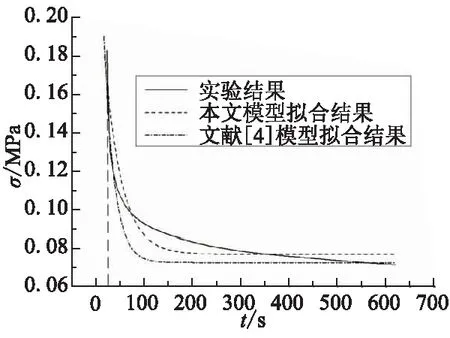
在加载段，t

σ11= 2(λ2-λ-1)[C10I1+2C20(I1-3)+3C30(I1-3)2]+

(17)

当t≥t0时，可得松弛阶段应力响应函数为

(18)

式中σ∞为材料在单轴等速拉伸到ε0的超弹响应，λ0=1+ε0。

利用式(18)可对松弛试验结果进行拟合，进而获取本构模型参数A1、A2、θ及σ∞，参数拟合结果见表1，拟合结果与实验结果如图3所示。

图3 松弛曲线试验及理论结果

由图3可看出，HTPB/IPDI弹性体在应变保持阶段初期松弛较快，但随着时间的增加，松弛速度逐渐降低，到600 s时应力已趋于平稳。本构模型拟合结果基本反映了材料的松弛特性，实验曲线的偏差主要表现在松弛曲线由快速松弛向趋于稳定的过渡阶段。这是由于松弛函数阶数较少导致的，但其拟合精度较文献[4]所用本构模型拟合精度有了大幅提高，同时并未增加模型的复杂程度。总之，通过对上述松弛模型和拟合方法的改进，保证了在静态和准静态条件下材料粘弹性特征的描述精度，确保了本构模型中参数的物理意义。

3.2 拉伸试验结果分析

本构中的参数C10、C20、C30可用单轴拉伸曲线拟合，拟合方程为式(17)，参数A1、A2、θ用松弛试验拟合的结果，对拉伸速率为12.5 mm/min的实验结果进行拟合，参数拟合结果见表1。

将表1中参数代入式(17)，可预测不同拉伸速率下HTPB/IPDI弹性体的应力应变关系。图4为拉伸速率为12.5、25、100 mm/min时的实验结果与本构模型所得结果的对比。由图4可看出，HTPB/IPDI弹性体的力学性能具有一定的率相关性，这与松弛特性所反应的粘弹特性是一致的；在初始阶段应力上升较快，随应变增加材料开始软化，模量减低。试验后发现，试验试件可完全恢复形貌，且完全恢复后，其几何尺寸没有显著变化，且粘弹性特征在小变形下不及大变形下明显。这也说明在小变形和短时间加载条件下HTPB/IPDI弹性体可直接用超弹性本构模型而忽略其粘弹性特征，但在大变形及长时间加载下其粘弹性特征是不能忽略的。所以，本文对HTPB/IPDI所做的粘-超弹性假设是合理的，预测结果与试验数据吻合较好,说明所建的本构模型能准确反映HTPB/IPDI弹性体在单轴加载下的粘-超弹性力学性能。

表1 本构中各参数拟合结果

图4 应力-工程应变曲线实验与预测结果

尽管如此，模型与实验数据存在着一定偏差，主要是由于2个原因造成的。一方面，在超弹本构模型中，应变能函数选用Yeoh模型，而Yeoh模型忽略了I2对应变能的影响，尽管有部分影响折算到I1中，但这种假设仍会造成模型的误差[9]。另一方面，如上所述，是松弛函数导致的。

4 结论

(1)实验结果显示，在静态及准静态加载下，HTPB/IPDI弹性体材料的率相关性及松弛特性明显，材料具有显著的粘弹性特征，加之材料的变形量较大，说明具有典型的粘-超弹性材料的特征。

(2)所建立的HTPB弹性体粘超弹性本构模型，由超弹与粘弹两部分组成；用松弛试验对粘弹部分的参数进行拟合，其他参数用速率为12.5 mm/min的拉伸曲线进行拟合，拟合结果与实验结果吻合较好。

(3)用拟合所得的参数，预测25 mm/min及100 mm/min下的单轴拉伸的实验结果，预测结果与实验结果吻合较好，说明本文所建立的模型能够较好地用于HTPB弹性体在有限变形下的力学性能描述中。

(4)所建立的本构模型较现有文献中应用的模型简单，用不同的实验结果拟合不同的参数，求解过程物理意义明确，适用于在该类材料研究及设计中的工程数值仿真应用。

参考文献：

[1] 邹德荣.双基推进剂用丁羟胶包覆层研究研制[J].含能材料,2004,12(1):52-55.

[2] Shu L H,He L,et al.Study on the finite element method for three-dimensional static property of polyurethane vibration isolators[J].Advanced Materials Research,2011,295:1586-1589.

[3] 刘柏峰,朱海潮,等.聚氨酯隔振器特性的有限元分析[J].噪声与振动控制,2010,1:131-135.

[4] Yang L M,Shim V P W,et al.A visco-hyperelastic approach to modeling the constitutive behavior of rubber[J].International Journal of Impact Engineering,2000,24(6-7):545-560.

[5] Shim V P W,Yang L M,et al.A visco-hyperelastic constitutive model to characterize both tensile and compressive behavior of rubber[J].Journal of Applied Polymer Science,2004:92(1):523-531.

[6] 周相荣,王强,王宝珍.一种基于Yeoh函数的非线性粘超弹本构模型及其在冲击仿真中的应用[J].振动与冲击,2007,26(5):33-38.

[7] Li C,J Lua.A hyper-viscoelastic constitutive model for polyurea[J].Materials Letters,2009,63(11):877-880.

[8] Pawlikowski M.Non-linear approach in visco-hyperelastic constitutive modeling of polyurethane nanocomposite[J].Mechanics of Time-Dependent Materials,2013:1-20.

[9] Yeoh O H.Some Forms of the strain energy function for rubber[J].Rubber Chemistry and Technology,1993,66(5):754-771.