大时宽带宽积雷达空间目标距离像估计
2014-03-13
(中国电子科技集团公司第三十八研究所,安徽合肥230088)
0 引言
随着空间活动的增多,与之俱来的空间碎片对在轨卫星构成巨大的安全威胁[1-2]。因此,为规避风险及满足未来空间作战需求,对空间目标进行探测、分类识别、定轨及编目等具有十分重要的现实意义[3-5]。空间目标成像为目标的分类识别提供了一种有效的解决方案[6]。而对目标进行高分辨一维距离成像,是对目标成像的前提条件之一[7]。为此,采用大时宽大带宽积信号,在满足探测威力的情况下亦能获得较高分辨的一维距离像,从而为空间目标探测及识别提供有效的技术支撑。
然而,由于空间目标的飞行速度通常高达十几甚至几十马赫,在信号时宽内,目标存在明显的跨距离单元的走动。此外,对于线性调频(LFM)信号,还存在严重的距离-多普勒耦合。这给目标一维距离像的提取带来难度。可利用速度和加速度的先验信息进行运动补偿。但是,在实际工作中,通常不便于获取目标的先验信息,或者获取的精度不满足运动补偿要求。文献[8]先发射点频信号获得目标径向速度;然后再发射大时宽大带宽积信号,利用前面估计的速度对当前回波信号进行运动补偿。通常由于空间目标具有较大的加速度,存在多普勒的变化。因此,需考虑速度变化对运动补偿的影响。为此,文献[9]对宽带信号回波采用基于立方相位函数法的参数估计,并考虑了径向速度的变化对距离像的影响。但是在运动补偿中,并未对一次相位项中的距离-多普勒耦合项进行解耦。
鉴于此,本文首先推导了具有大时宽带宽积的LFM信号下的空间目标回波模型,并讨论了采用传统脉压处理后的数学表达式,以给出不适合传统脉压处理的定量条件。然后,采用二次相位滤波的方法[10]获得目标径向速度和加速度,并进行包括距离-多普勒在内的运动补偿,获得较高分辨的空间目标一维距离像,为空间目标的分类识别、定轨和编目提供理论支持。结合理论分析,最后通过计算机仿真实验佐证方法的有效性。
1 空间目标回波特征分析
1.1 回波模型
设雷达发射信号为LFM信号,表示为
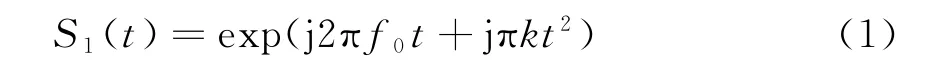
式中,f0为发射信号载频;k为LFM信号调频率;|t|≤T/2,T为发射信号脉冲宽度。设在时间T内,目标作加速度为a的匀加速直线运动,则目标回波接收时刻t与信号发射时刻t0之间的关系可表示为

式中,R0为目标和雷达间的初始斜距,v0为目标初始径向速度。
令ε=(c-v0)/(c+v0)。通常情况下由于|v0/c|≪1,则式(2)中
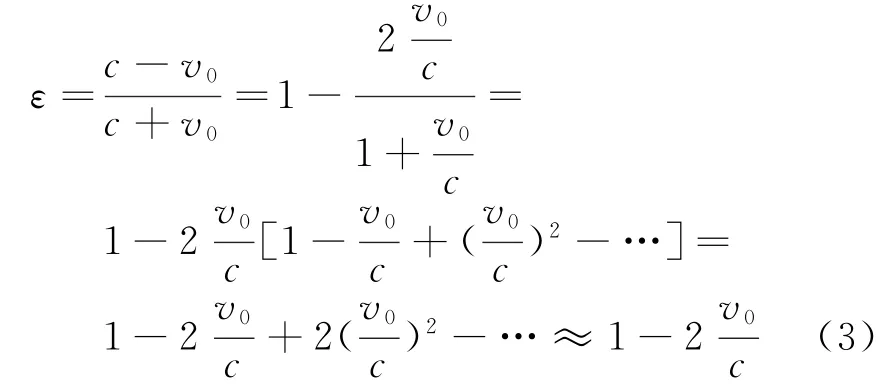
同理2R0/(c+v0)≈2R0/c。则式(2)可简化为

从而回波信号可表示为
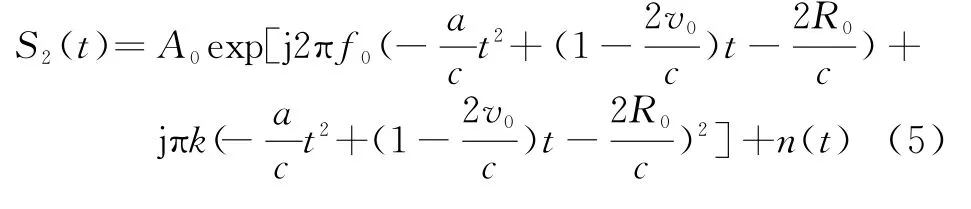
式中,A0为回波幅度常数;n(t)为加性复高斯白噪声。对式(5)所示的回波信号进行下变频处理并忽略4次及以上次方的相位项[9],最后可得
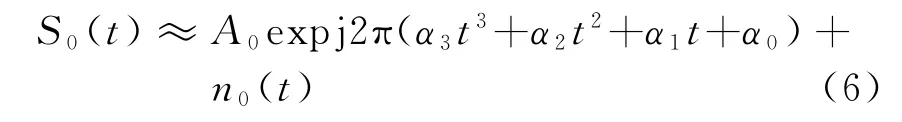
式中,n0(t)为混频后高斯白噪声,且相应系数及常数项如下:
1.2 脉压处理
为了讨论采用传统脉冲压缩方法处理大时宽带宽积信号下的空间目标回波,不失一般性,设在发射信号期间目标为匀速直线运动,则目标回波为[11]
式中,rect(·)为矩形函数;τ0=2R0/c。则由式(1)和式(8)可得采用传统匹配滤波器处理,可得[12]
式中,E{·}为{·}的期望运算;B为发射信号带宽;U为脉压后能量最大值;fd为多普勒偏移量。以便进一步讨论回波经传统匹配滤波器处理后一维距离像的影响,令式(9)中fd=0,可得


综合式(10)和式(11),可得大时宽带宽积回波信号采用传统匹配滤波器处理后的损失。由此可知,如需获得所期望的目标一维距离像,需估计出能满足精度要求的运动参数。
2 空间目标一维距离像获取
2.1 运动参数估计
从式(6)可知经下变频后的目标回波的相位近似为三次方项,因此,采用三次方相位项系数的估计方法获得目标运动参数。设信号表示为

式中,Zω(n)表示功率为σ2的复高斯白噪声;N为离散点数;{β0,β1,β2,β3}为待估计的参数。由文献[10]构造的三次方相位函数为

结合式(12),式(13)中zr(n+m)zr(n-m)可表示为[10]

其中第一项为信号函数分量,且其二次项系数2(β2+3β3n)为信号的瞬时频率变化率,表示为

由于信号频率变化率与二次项系数对应,则对信号频率变化率的估计等价于对信号二次项系数的估计,可通过二次相位滤波器组的方法提取二次相位项系数[10]。
由式(13)可知,选取两个不同的离散时间n1和n2,可计算分别在n1和n2下随Ω变化的峰值,从而
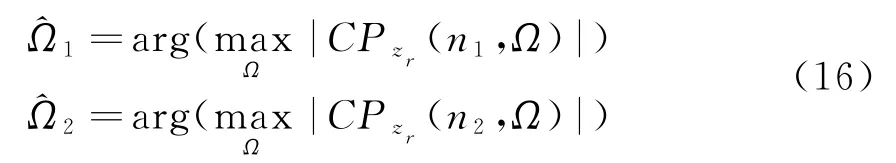
式中,arg(·)表示子集。由式(15)和式(16)可得二次和三次相位项系数估计值为
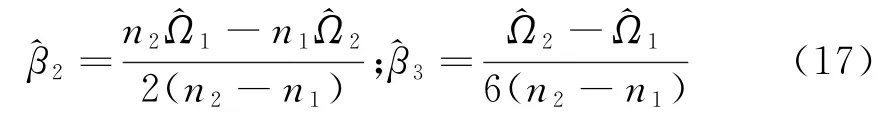
2.2 一维距离像
由文献[10]可知,式(17)中n1和n2分别取0和0.11N。利用式(17)中估计的系数,对式(8)中二次和三次项进行补偿,得如果进行如式(18)的补偿处理后直接进行FFT处理,获得的距离像存在距离-多普勒耦合,导致目标真实距离发生偏移,因此需进一步解距离-多普勒耦合。
由式(7)中α3=-ka(c-2v0)/c2=-ka/c+2kav0/c2≈-ka/c,以及,则根据式(17)可得目标加速度和径向速度估计值分别为
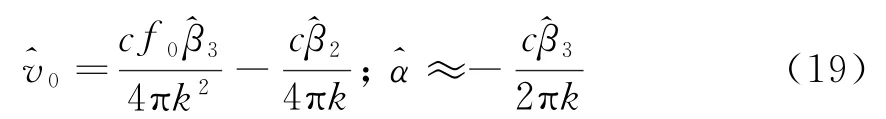
由式(19)中速度估计值0,可补偿式(18)中的距离-多普勒耦合项

由于式(20)中一次项系数两分量有|-2R0k/c|/|4v0k R0/c2|≫1,则式(20)可近似为
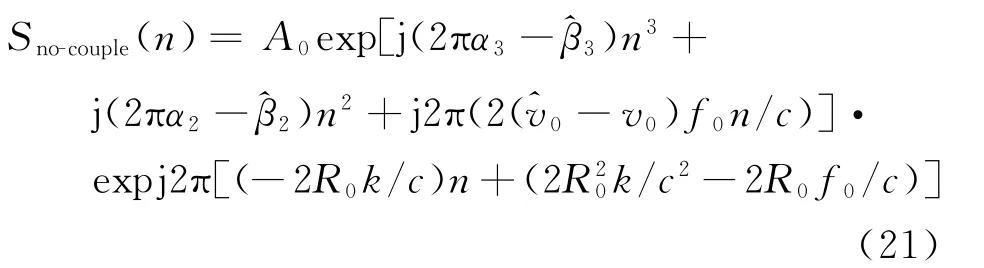
则由式(21)可得目标一维距离像

式中,

3 计算机仿真试验
3.1 传统脉压处理试验
分析采取传统的匹配滤波处理时对应的输出特性。由式(11)可知,目标回波对应的匹配滤波器输出的峰值与BT|2v/c|变化关系。
从图1可知,当BT|2v/c|在1附近或小于1时,匹配滤波器输出峰值基本保持在较平稳的状态。但当BT|2v/c|大于1且逐渐增大时,其峰值迅速下降,例如当BT|2v/c|为10时,峰值下降约10 d B。
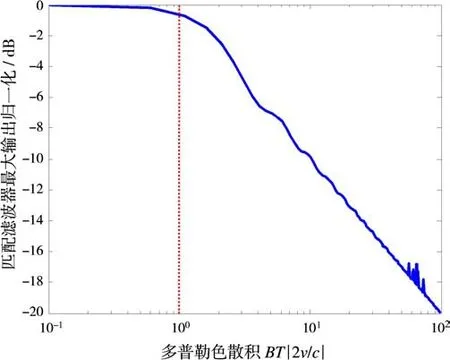
图1 匹配滤波器输出最大值(归一化)与多普勒色散积BT|2v/c|关系
然而,对于具有大时宽带宽积(BT)雷达而言,通常由于空间目标高速飞行,因此存在相对径向运动的目标极易获得比1大得多的BT|2v/c|值,例如:B,T和v分别为50 MHz、40 ms和5000 m/s时,对应BT|2v/c|约为67。此时,若仍采用传统脉压处理方法势必会导致包括目标距离像在内的相关性能急剧下降。
3.2 一维距离像的提取
设雷达发射信号带宽B为5 M Hz,脉冲宽度T为20 ms,则LFM信号调频率k为B/T=2.5×108Hz/s,载频f0为2.6 GHz;目标初始径向速度v0为8×103m/s,加速度a为50 m/s2。回波信噪比SNR为-10 dB。
现分析LFM回波信号分别在不进行运动补偿及对二次和三次相位项进行补偿两种情况,目标径向速度从0 m/s到1×104m/s变化时的脉压处理损失(速度为0时的脉压峰值与当前速度下脉压峰值之比,再取对数)如图2所示。
从图2可知,当不进行任何运动补偿,而直接对回波进行脉压处理时,脉压损失随目标径向速度增大而增大。当径向速度为8×103m/s时,脉压损失约为3 dB。而对回波的二次和三次相位项进行运动补偿后,脉压损失有所下降,但是当径向速度大于1×103m/s时,随径向速度增大,脉压损失增幅较缓慢。由此可知,对高径向速度的空间目标而言,在获取目标距离像之前需进行二次及以上次的相位项进行补偿,以减少脉压处理损失。
设分别位于800 km+10ΔR及800 km+30ΔR位置的两个目标,其中ΔR为距离分辨单元。未经运动补偿而直接进行脉压处理后获得的目标距离像如图3所示。
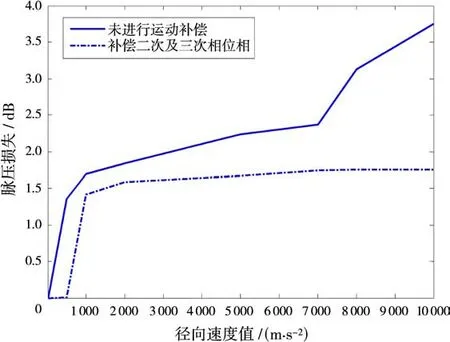
图2 不进行运动补偿及对二次和三次相位项进行补偿时脉压损失比较
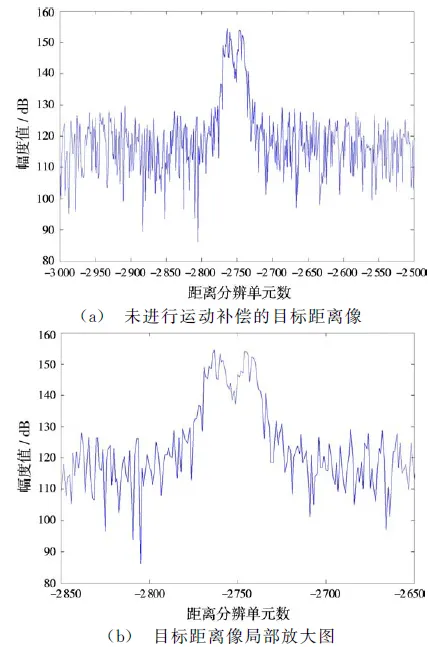
图3 未进行运动补偿的目标距离像
从图3可以看出,目标距离像发生了扩展及畸变,已失去了目标距离信息,在距离维不能分辨。因此,利用如式(19)所示的运动参数的估计值,对回波二次及三次相位项进行补偿后获得的距离像如图4所示。
从图4可知,进行补偿后可分辨出两个目标的距离像,没有如图3所示的距离像畸变。但是图4中距离像较目标初始距离发生了距离走动,因此需进一步补偿回波相位项中如式(18)所示的距离-多普勒耦合项。在图4基础上进一步对距离-多普勒耦合进行补偿后的距离像如图5所示。

图4 对二次和三次相位项进行补偿后的目标距离像
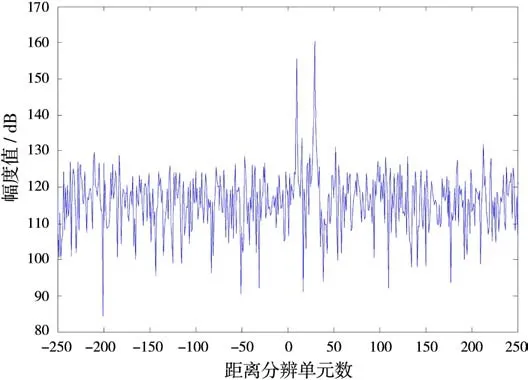
图5 进行运动补偿后的目标距离像
从利用如式(22)进行运动补偿后获得如图5所示的目标距离像可看出,能清晰分辨距离维不同距离单元的目标,且未出现如图4所示的距离走动。
由此,可看出采用式(19)所示的参数估计值进行运动补偿后可获得较高分辨的目标距离像。
4 结束语
本文推导了具有大时宽带宽积LFM信号的空间目标的回波模型。根据回波模型,采用二次相位滤波器方法提取回波信号的二次项及三次项相位系数,解算出目标的径向速度及加速度值。利用如上测量信息对回波进行包括距离-多普勒耦合在内的运动补偿,从而可获得目标距离像。通过计算机仿真试验中对脉压处理损失以及补偿前后距离像的比较分析,验证了本文估计空间目标一维距离像的有效性。
[1]LI Hongwei,HAN Jianwei,HUANG Jiangguo,et al.Primary Research of Small Space Debris Impact Inducing Discharge[J].IEEE Trans on Plasma Science,2013,41(12):3410-3415.
[2]FUKUSHIGE S,AKAHOSHI Y,WATANABE K,et al.Solar Array Arcing Due to Plasma Created by Space-Debris Impact[J].IEEE Trans on Plasma Science,2008,36(5):2434-2439.
[3]DU Lan,LIU Hongwei,BAO Zheng,et al.Radar HRRP Target Recognition Based on Higher Order Spectra[J].IEEE Trans on Signal Processing,2005,53(7):2359-2368.
[4]AKGUN T,ALTUNBASAK Y,MERSEREAU R M.Super-Resolution Reconstruction of Hyperspectral Images[J].IEEE Trans on Image Processing,2005,14(11):1860-1875.
[5]贾高伟,常文革.分布式雷达空间目标定位系统性能分析[J].雷达科学与技术,2010,8(3):199-203.
[6]XING Mengdao,WANG Qi,WANG Genyuan,et al.A Matched-Filter-Bank-Based 3-D Imaging Algorithm for Rapidly Spinning Targets[J].IEEE Trans on Geoscience and Remote Sensing,2009,47(7):2106-2113.
[7]KIM K T.Focusing of High Range Resolution Profiles of Moving Targets Using Stepped Frequency Waveforms[J].IET Radar,Sonar&Navigation,2010,4(4):564-575.
[8]王启智.大时宽带宽积信号匹配滤波研究[J].空军预警学院学报,2013,27(4):246-248.
[9]刘红超,纠博,刘宏伟,等.一种匀加速空间目标高分辨距离像补偿算法[J].西安电子科技大学学报(自然科学版),2012,39(4):81-86.
[10]O’SHEA P.A Fast Algorithm for Estimating the Parameters of a Quadratic FM Signal[J].IEEE Trans on Signal Processing,2004,52(2):385-393.
[11]WEISS L G.Wavelets and Wideband Correlation Processing[J].IEEE Signal Processing Magazine,1994,11(1):13-32.
[12]杨利民.超宽带雷达目标探测技术研究[D].南京:南京理工大学,2012.
