一种改进的JIPDA多目标跟踪算法

(空军预警学院,湖北武汉430019)

0 引言

采用二次差频测距方式的多频连续波雷达是在连续波双频测距的理论基础上发展起来的一种新体制雷达,该体制雷达可用于多目标的高精度测量与跟踪,并具有设备简单、运算量小、便于同时测速测距等优点,近年来越来越受到人们的重视[1-3]。

JIPDA[4]算法是杂波环境下对多目标进行数据互联的一种良好算法,其原理与JPDA[5-7]算法类似,该算法也是基于确认区域内的所有量测为其计算一个加权残差用于目标状态的更新。不同之处在于JPDA算法本身默认了目标一定存在,所以JPDA算法无法提供任何目标存在概率的信息,而JIPDA算法在形式上类似于IPDA[8-9]算法,其考虑了目标存在概率(包括存在并可检测的概率和存在但不可检测的概率),并且依据目标存在状态的变化是一个马尔科夫过程将JIPDA算法分为两类,分别是一类马尔科夫JIPDA算法和二类马尔科夫JIPDA算法。除此之外,根据虚假量测的空间密度是否已知,JIPDA滤波器有两种形式。其中非参数JIPDA滤波器利用一种有效的观测区域体积和落入该区域虚假量测数的估计方法来求取联合事件的后验概率,避免了非参数JPDA滤波器必须利用整个确认区域体积以及落入该区域的虚假量测总数进行计算。对于参数JIPDA滤波器也不必像参数JPDA滤波器需假设虚假量测的空间密度是恒定不变的,它允许空间的虚假量测密度是非均匀的[4],这使得算法的运用更加灵活。

本文利用多频连续波雷达能提供高精度径向速度参数的优势,提出了含径向速度量测的改进JIPDA滤波跟踪算法,通过Monte Carlo仿真验证了所提算法的有效性。

1 传统JIPDA算法

1.1 JIPDA算法分类

设Z(k)为k时刻落入各个目标跟踪波门的候选回波集合,Z k为直到k时刻的确认量测的累积集合,即

定义与航迹存在性相关的事件如下：

表示k时刻目标t存在;

表示k时刻目标t不存在。

若把这两个事件看作一个具有两个状态的马尔科夫链,即一类马尔科夫链,它们相应的概率表示为和,且定义状态转移概率矩阵P1为

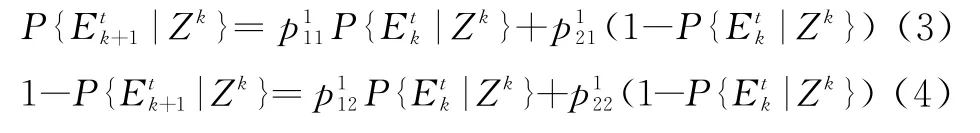
对于二类马尔科夫链的JIPDA算法,需要同时考虑目标存在性和可见性,则与目标存在性有关的事件定义如下：

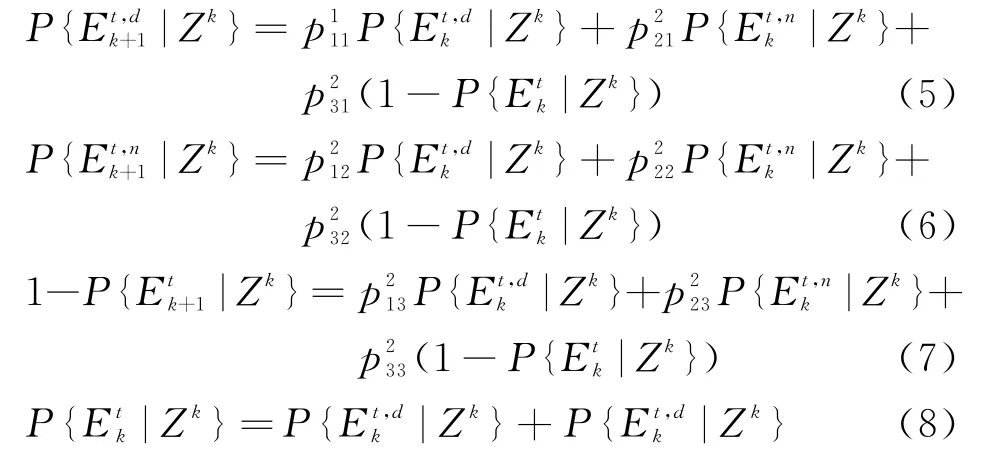
此时状态转移概率矩阵P2定义为

注意到,一类马尔科夫链JIPDA算法可看作是把二类马尔科夫链JIPDA算法中的用代替,用0代替,所以下文仅围绕二类马尔科夫链JIPDA算法进行介绍,一类马尔科夫链JIPDA算法可类似推导。

1.2 杂波估计

雷达目标跟踪中,某测量时刻k,在杂波环境中有T个空中目标,设落入目标t跟踪波门的虚假量测数表示为,并假设虚假量测是在以正确的量测为中心的正方形内均匀产生的,则落入确认区域内的虚假量测数近似服从泊松分布,当杂波密度λ已知时,有

式中,V k表示k时刻各目标跟踪波门的联合确认区域。

当杂波密度λ未知时,有

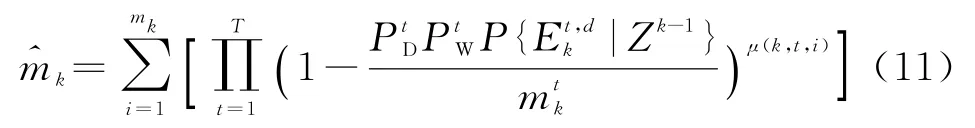
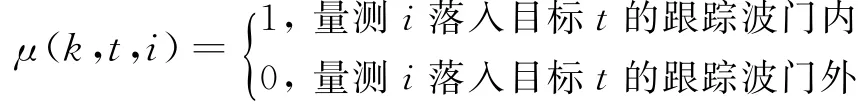
此时,各目标跟踪波门的联合确认区域V k可以近似表示为

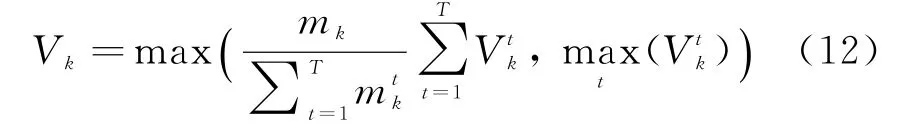
1.3 JIPDA算法数据互联

JIPDA算法数据互联的目的就是计算每一个量测与其可能的各种源目标相互联的概率。在有量测落入不同目标跟踪波门的重叠区域内的时候,则必须考虑各个量测的目标来源情况。首先产生联合事件,方法与JPDA算法相同,需依据以下两个基本原则：

(1)每个量测只能有一个源;

(2)每个目标最多只能对应一个量测。

假设E i表示第i个联合事件,X表示联合事件总数,并定义和分别表示联合事件E i中没有量测相对应和只有一个量测相对应的目标的集合。则非参数JIPDA算法的联合事件后验概率为

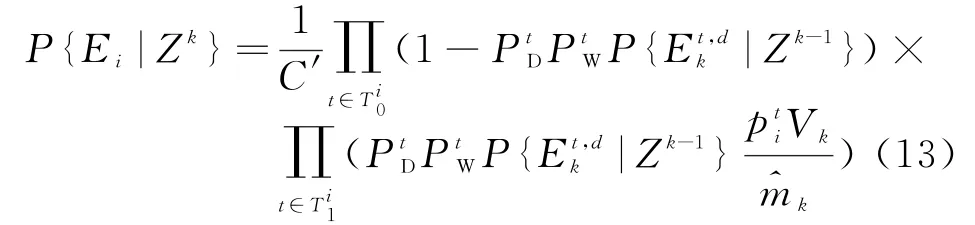
式中,C′是归一化常数,表示联合事件E i中与目标t互联的量测m(i,t)的位置先验概率密度,它近似服从截断高斯分布[10]。

参数JIPDA算法的联合事件后验概率为

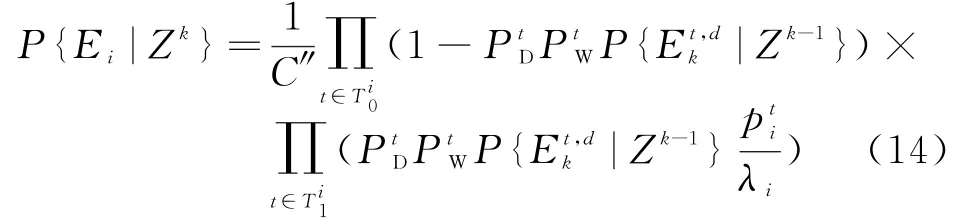
式中,C″亦为归一化常数,λi=λ(z m(i,t))表示量测m(i,t)所处空间的虚假量测密度。

在此基础上,可以通过符合条件的联合事件后验概率求和得到与目标t相关事件的后验概率,并定义Ξ(t,i)表示量测i源于目标t的联合事件,而联合事件Ξ(t,0)则表示没有量测源于目标t。

那么没有量测源于目标t的后验概率为

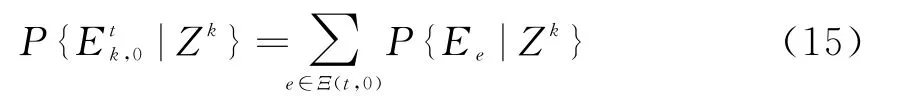
目标t存在但未被检测到的后验概率为

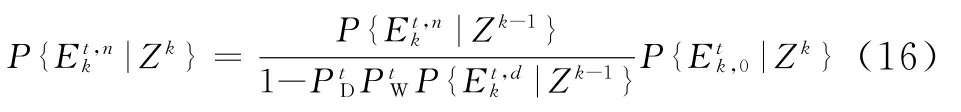
目标t存在并可以被检测到,但没有量测源于该目标的后验概率为

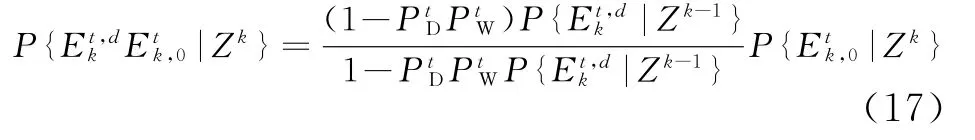
目标t存在并可以被检测到,且量测i源于该目标的后验概率为

目标t存在并可以被检测到的后验概率为

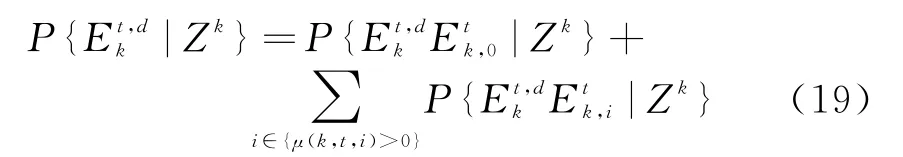
式中,{μ(k,t,i)＞0}表示k时刻落入目标t跟踪波门内的量测集合。

由式(8)和式(15)～(19)可得,不同量测与目标t的互联概率为

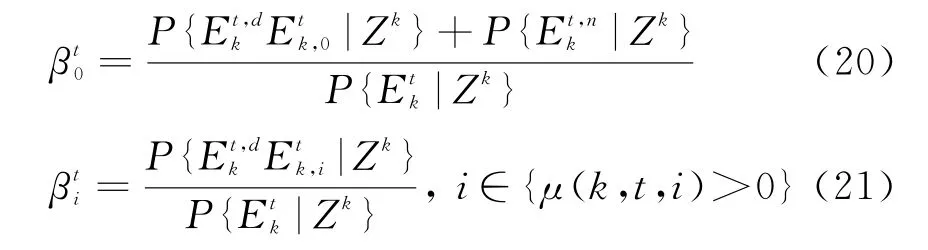
2 含径向速度的改进JIPDA算法

2.1 目标跟踪模型

设被跟踪目标在二维平面内作匀速直线运动,则基于改进JIPDA算法的目标t的状态方程可以表示为

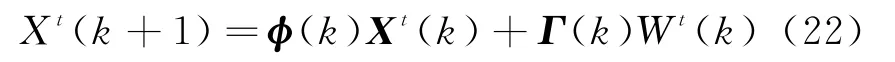
对于连续波雷达,雷达测量是在极坐标系下进行的,其位置量测(距离和方位角)、径向速度量测分别为r l,θl和,则k时刻目标t的量测方程为

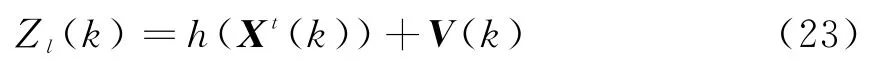
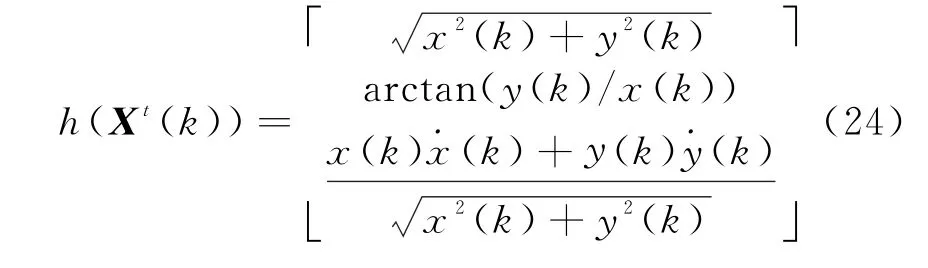
2.2 坐标变换

在传统的雷达目标跟踪中,常常在直角坐标系下描述目标的运动方程,而连续波雷达的量测值是在极坐标系下得到的,需用坐标变换的方法将极坐标系下的量测值转换到直角坐标系下。

文中利用的无偏量测转换技术[8]可方便地实现坐标变换。得到直角坐标系下含径向速度的量测向量z l(k)=[x l(k)y l(k)(k)]T。其中,

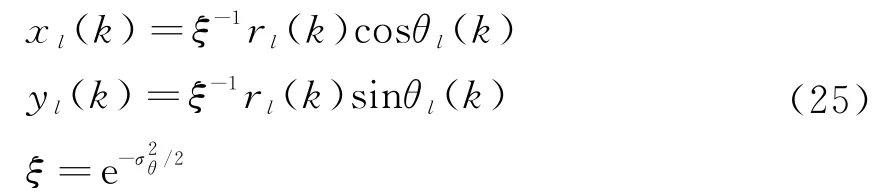
坐标变换后的观测矩阵其中

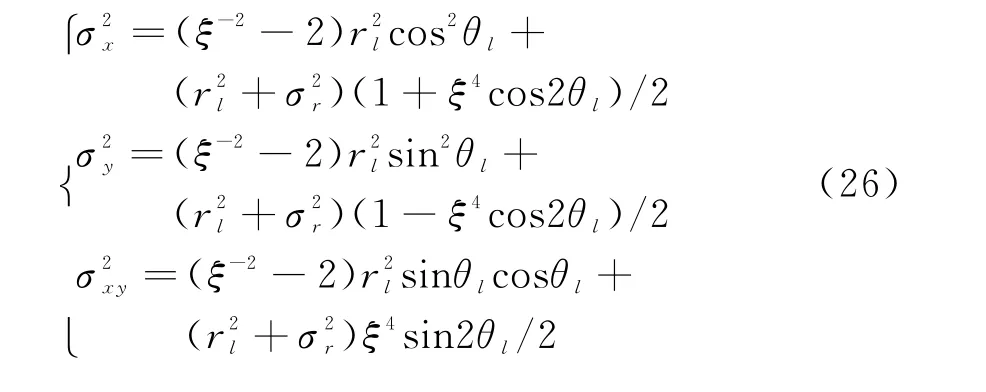
2.3 观测矩阵

经过坐标变换后,观测矩阵h c(X t(k))仍然是非线性的,需要进行线性化处理,通常的做法是将含径向速度的非线性函数h c(X t(k))在状态预测值X t(k|k-1)处用泰勒级数展开,忽略二阶以上的项,则可得到此时的观测矩阵

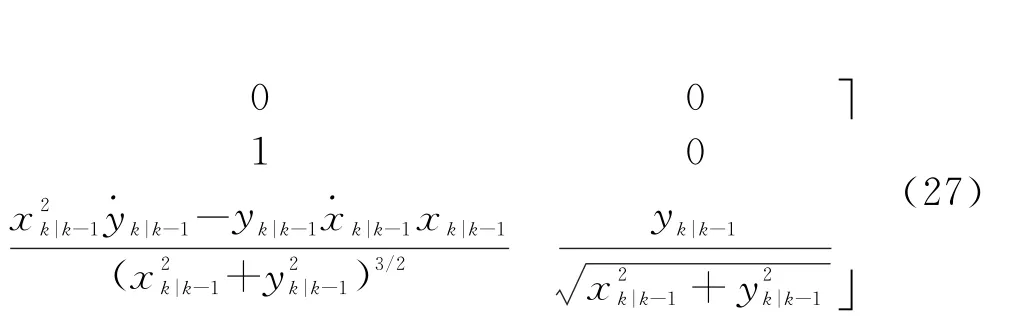
2.4 跟踪滤波

在得到不同量测与目标t的互联概率后,以其为权值开始滤波,主要有以下几个步骤组成。

(1)状态和误差协方差矩阵的预测

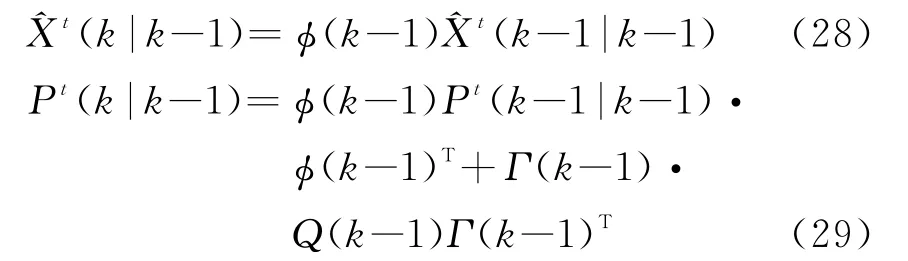
(2)建立跟踪波门

含径向速度量测的跟踪波门是在每个扫描时刻围绕目标的状态预测值建立的,它能够进一步限制有效量测的数量,进而减少航迹关联中候选关联的数量,表达式为

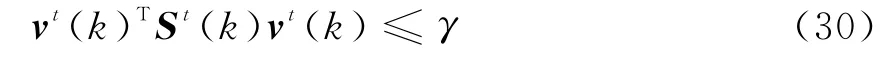
式中,跟踪门限γ服从自由度为3的卡方分布,v t(k)表示目标t的组合新息,S t(k)表示目标t的新息协方差矩阵,且满足

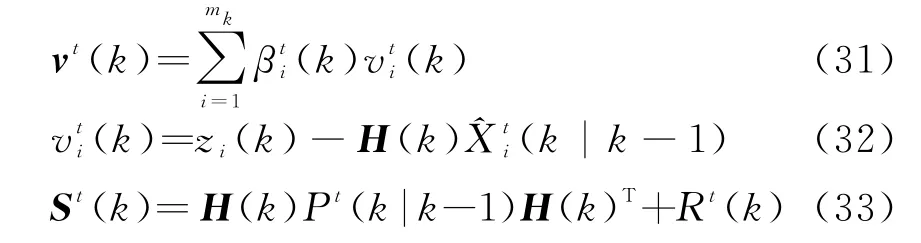
式中,H(k)为坐标变换后含径向速度量测的观测矩阵。

(3)滤波增益

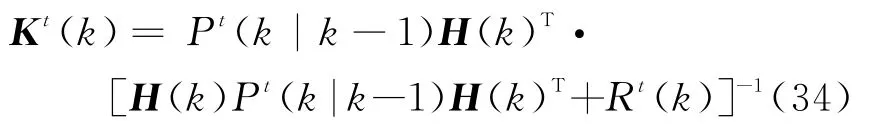
(4)状态和误差协方差矩阵的更新

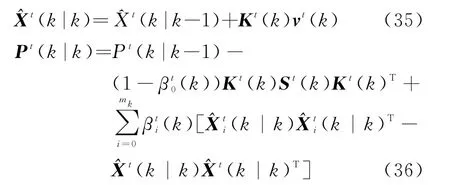
3 仿真分析

假设雷达跟踪两个交叉运动的目标,并选取CV模型描述目标的运动状态,目标的初始位置分别为：目标1(-29.5km,400m/s,34.5km,-400m/s);目标2(-26.25km,296m/s,34.5 km,-400m/s)。过程噪声标准差q1=q2=0.01;目标测距、测角及径向速度的量测标准差分别为σr=200 m,σθ=0.01 rad,;目标的检测概率PD=0.9,门概率PG=0.9999;采样间隔Ts=1 s。

在整个观测空间中设定了两块高杂波密度区域,分别为(xmin,xmax,ymin,ymax)=(-25 000,-23 500,28500,30000)m和(-24000,-23500,30 500,31 400)m,并假设这两块高杂波密度区域的单位面积虚假量测数为2×10-7,其他区域的单位面积虚假量测数为1×10-7。杂波的位置产生方法参见文献[8],径向速度为最大值40 m/s的均匀分布。实验中采用第一类马尔科夫链,并假设转移概率矩阵,目标初始存在概率,Monte Carlo仿真次数为100次。

图1(a)为目标的真实航迹与是否引入径向速度量测两种情况的JIPDA算法的滤波航迹对比,不难看出,在杂波环境下两种算法均可对复杂的目标进行良好的跟踪,图1(b)给出了航迹形成初始阶段的局部放大图,从图中可以看出,改进JIPDA算法在航迹形成初始阶段的跟踪性能上有了较大改善。

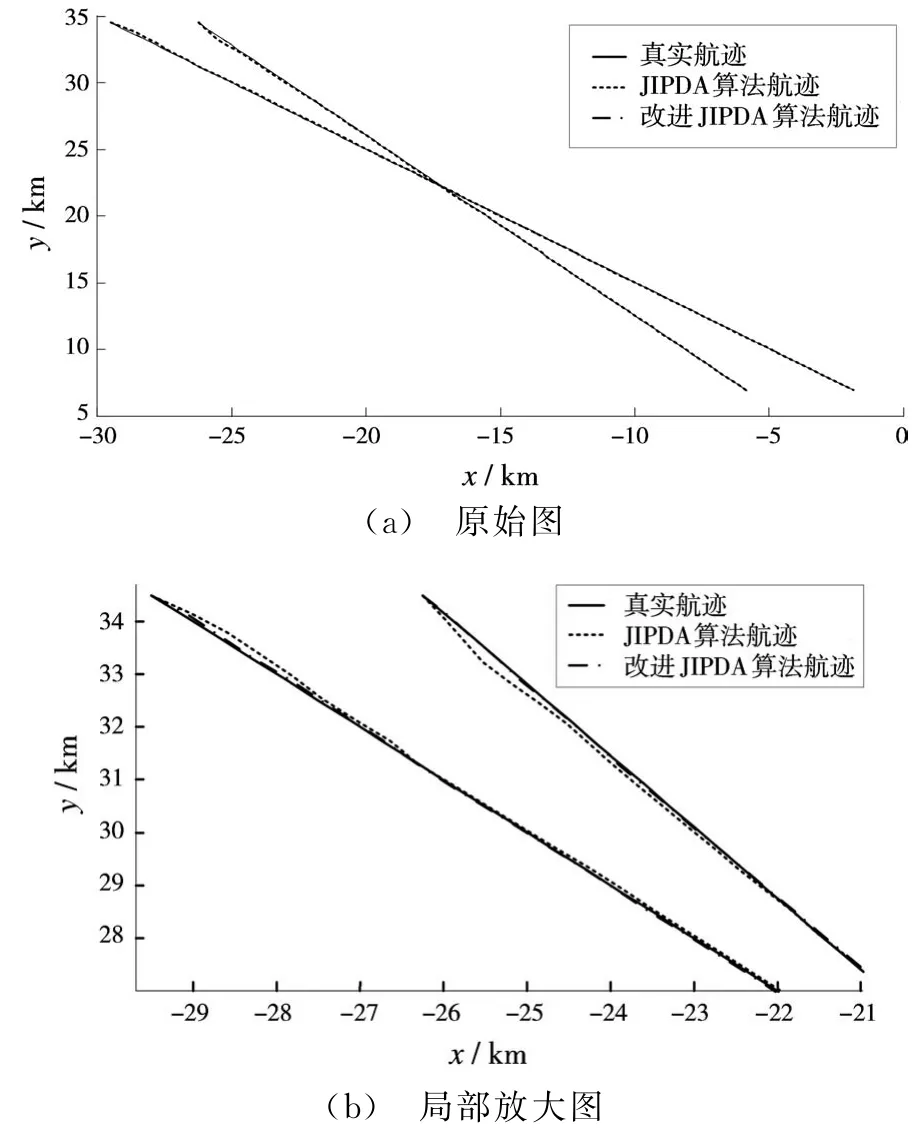
图1 滤波航迹对比

进一步比较JIPDA算法及改进JIPDA算法中位置和速度的滤波误差RMS,分别如图2～图5所示,可见当引入径向速度时,改进的JIPDA算法的滤波误差较小,跟踪性能较优,且引入径向速度时收敛速度要比不引入径向速度时快。除此之外,从图中可以明显地看出,改进JIPDA算法的均方根误差随着径向速度量测精度的提高而减小,即跟踪的准确性更高。

由于径向速度量测的利用,使得改进JIPDA算法在航迹关联中的候选关联数量减少,进而缩短了算法的计算时间,表1给出了是否引入径向速度量测两种情况的每扫描周期耗时平均值,通过比较,更加直观地反映了改进JIPDA算法在计算时间上有了较大进步。

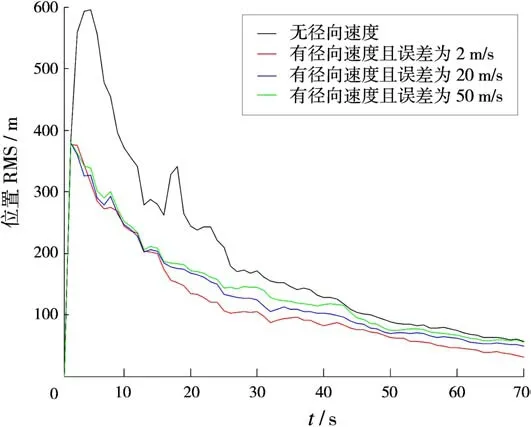
图2 目标1的位置均方根误差

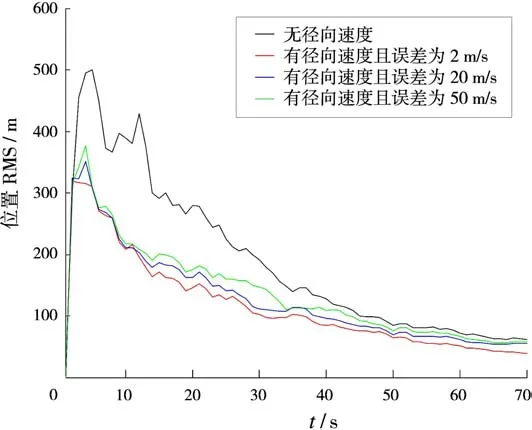
图3 目标2的位置均方根误差

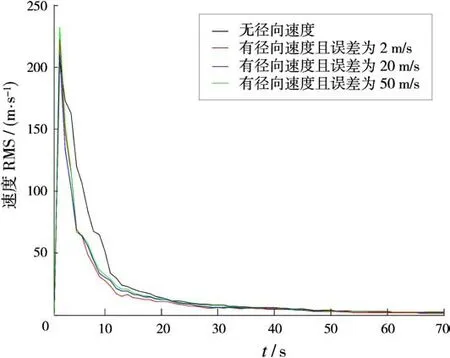
图4 目标1的速度均方根误差

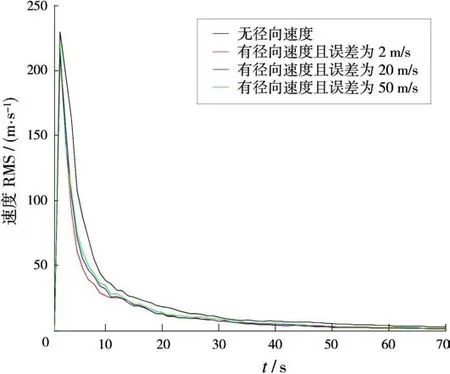
图5 目标2的速度均方根误差

表1 有无径向速度时每扫描周期平均计算耗时对比

4 结束语

本文针对多频连续波雷达的特点,提出了一种引入径向速度量测的改进JIPDA算法,并成功运用于杂波环境下的多目标跟踪。通过理论分析,并结合Monte Carlo仿真验证了算法的有效性。仿真结果表明,引入径向速度量测的JIPDA算法在跟踪精度上优于传统的JIPDA算法,且在计算耗时上有了较大改善。

[1]袁俊泉.连续波测距雷达信号分析器设计及相关理论与算法研究[D].长沙：国防科技大学,2004.

[2]黄燕群,黄勇,蔡睿洁,等.基于调频连续波雷达目标信号处理器研究[J].弹箭与制导学报,2012,32(5)：183-186.

[3]王怡然,常文革,田海山.RapidIO技术在高速信号处理系统中的应用[J].雷达科学与技术,2013,11(4)：390-394.WANG Yi-ran,CHANG Wen-ge,TIAN Hai-shan.Application of Rapid IO Technology in High Speed Signal Processing System[J].Radar Science and Technology,2013,11(4)：390-394.(in Chinese)

[4]MUSICKI D,EVANS R.Joint Integrated Probabilistic Data Association：JIPDA[J].IEEE Trans on Aerospace and Electronic Systems,2004,40(3)：1093-1099.

[5]尹帅,袁俊泉,吴顺华.一种利用径向速度信息的改进JPDA算法[J].空军预警学院学报,2013,27(5)：351-354.

[6]陈松.基于JPDA的多目标跟踪算法及其应用[J].电子测试,2012(8)：24-27.

[7]FORTMANN T E,BAR-SHALOM Y,SCHEFFE M.Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J].IEEE Journal of Oceanic Engineering,1983,8(3)：173-184.

[8]何友,修建娟,关欣,等.雷达数据处理及应用(第三版)[M].北京：电子工业出版社,2013：92-99,147-157.

[9]MUSICKI D,EVANS R,STANKOVIC S.Integrated Probabilistic Data Association[J].IEEE Trans on Automatic Control,1994,39(6)：1237-1241.

[10]BAR-SHALOM Y,TSE E.Tracking in a Cluttered Environment with Probabilistic Data Association[J].Automatica,1975,11(5)：451-460.