基于分段运动特性的空间目标检测算法

(国防科技大学自动目标识别国家重点实验室,湖南长沙410073)

0 引言

空间目标根据轨道高度的不同可分为低地球轨道、地球同步轨道、半同步轨道以及大椭圆轨道这四类目标[1]。不同区域的空间目标有着不同的用途。例如,气象、侦察、监视、资源、通信等卫星主要集中在卫星分布最密集的低轨道区域。又如,备受关注的美国的全球定位系统和俄罗斯的全球导航卫星系统都位于轨道高度约为20 000 km的半同步轨道。由于空间目标在军事和民用方面的广泛应用,使得对空探测问题越来越受到国内外学者的关注。

目前可实现空间目标检测的地基雷达系统分单基地和双(多)基地的情况[2]。对于双基地雷达,其收发异地,接收机静默工作的特点使得它在抗干扰和杂波抑制方面的性能明显优于单基地雷达。此外,双基地雷达在反隐身及生存能力方面与单基地雷达相比也存在一些突出优势。对用于卫星测控与通信的大型阵列天线而言,增加一个雷达站就可以构成双基地的空间目标探测系统,灵活地实现低成本的对空探测。因此利用双基地雷达实现对空探测越来越成为国内外的研究热点。

双基地雷达对空探测往往需要回波能量的积累才能使信噪比达到一定检测概率的要求。在此过程中有两个突出问题需要解决。第一,空间目标在雷达视场内相对雷达的运动规律不能用一阶或二阶模型统一表示,运动模型建立会相对复杂。第二,由于空间目标的快速运动,使得在长时间积累过程中很容易出现跨距离单元走动[3]和跨多普勒单元走动[4]的问题。

针对上述问题,本文以双基地雷达对空探测为研究内容,在分析了双基地雷达-空间目标三维模型的基础之上,利用空间目标经过雷达视场时的分段运动特性实现积累检测。本文将仰角较小的时间段定义为阶段一,近似为匀速直线运动。仰角较大时定义为阶段二,近似为匀加速直线运动[3]。介于两者之间为阶段三,该阶段内目标处于变加速运动状态。阶段一采用两级速度补偿的方法解决跨距离单元走动问题。阶段二因其时间短且回波信噪比较高,直接非相参积累即可检测到目标。阶段三采取帧分割,简化目标运动,帧内使用与阶段二类似的方法实现相参积累,重现目标轨迹。

1 空间目标的轨道特征及回波信号建模

1.1 空间目标的轨道特征

图1为双基地雷达-空间目标的空间三维图,坐标系选取ECF(Earth Centered Earth Fixed)坐标系。其中O为地球球心,T为发射站,R为接收站,S0为观测仰角最大时目标的位置,设该时刻为t0,此时星下点在E处。S为t时刻目标位置,其星下点在D处,星下点轨迹为图中弧形虚线。

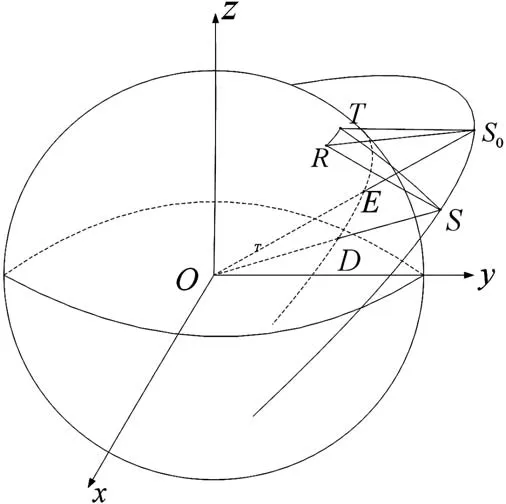
图1 双基地雷达-空间目标的几何关系图

图2中R为接收站位置,RE为地球半径,Rh为地球球心与目标的距离,θ(t),γ(t)和d(t)分别表示t时刻雷达仰角,目标相对接收站的地心角以及目标与接收站的距离。

图2 空间角度关系

图2左图中,由几何关系可得以下式子成立：

图2右图中,根据球面余弦定理有

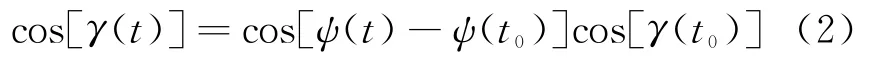
式(2)代入式(1)后求导得目标相对雷达接收站径向速度表达式[5]：

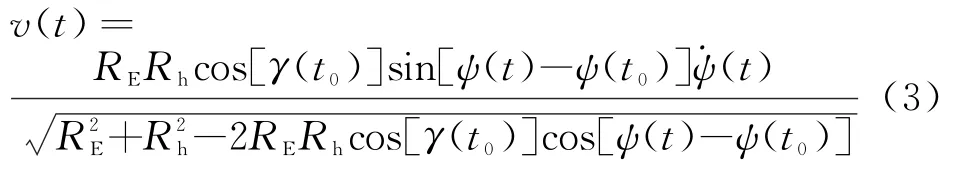
式中,(t)表示目标在ECF坐标系中的角速度,文献[6]中将其表达式近似为

ω′S为目标在ECI(Earth Centered Inertial)坐标系下的角速度,由轨道高度决定;ωE为地球自转角速度;I为轨道倾角。则目标在ECF坐标系下的角速度由轨道参数确定,不随时间变化。将(t)用ω′F代替后对式(3)求导便得目标相对雷达的径向加速度表达式[6]

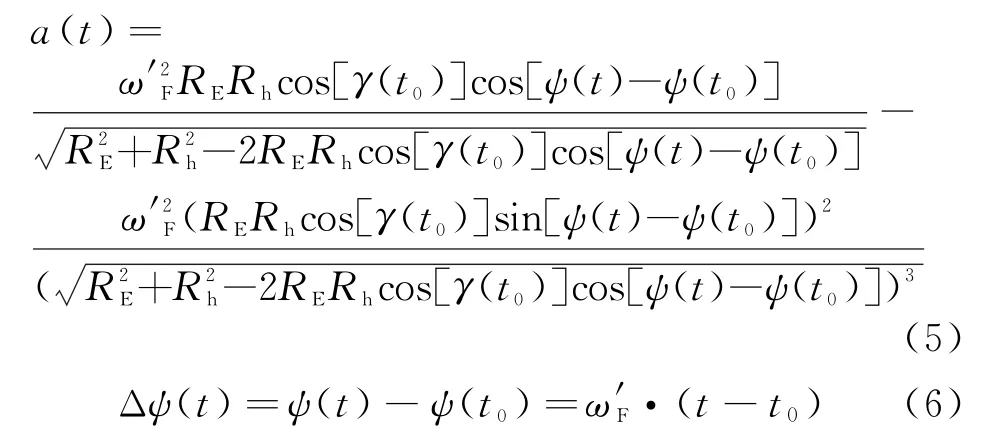
本文以ISS为例研究空间目标经过雷达视场的运动规律。根据式(4)、(5)和公开的ISS相关参数可描出ISS某次经过地面某接收站时相对接收站的径向速度、加速度随时间的变化曲线,如图3和图4所示。图中时间起点对应仰角最小时刻。

根据图3、图4,可将ISS经过雷达视场时的运动状态划分为三个阶段。在仰角较小时,径向速度较大,加速度近乎为零,可近似为匀速直线运动,对应ISS出现于雷达视场后前30 s内的状态,本文将其定义为阶段一。在仰角较大时,径向速度出现过零点,且此时加速度斜率近乎为零。根据文献[5-6]的分析,该过程可近似为匀加速直线运动,且与ISS出现于视场后第310～330s的状态对应,本文定义为阶段二。目标在上述两个阶段之间作变加速曲线运动,运动状态复杂,但在短时间内可以近似为匀速直线运动,本文将其定义为阶段三。

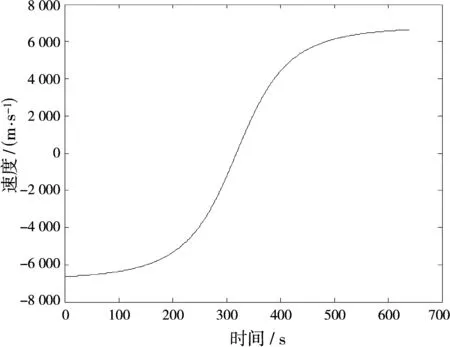
图3 ISS某次穿越雷达视场径向速度时间关系

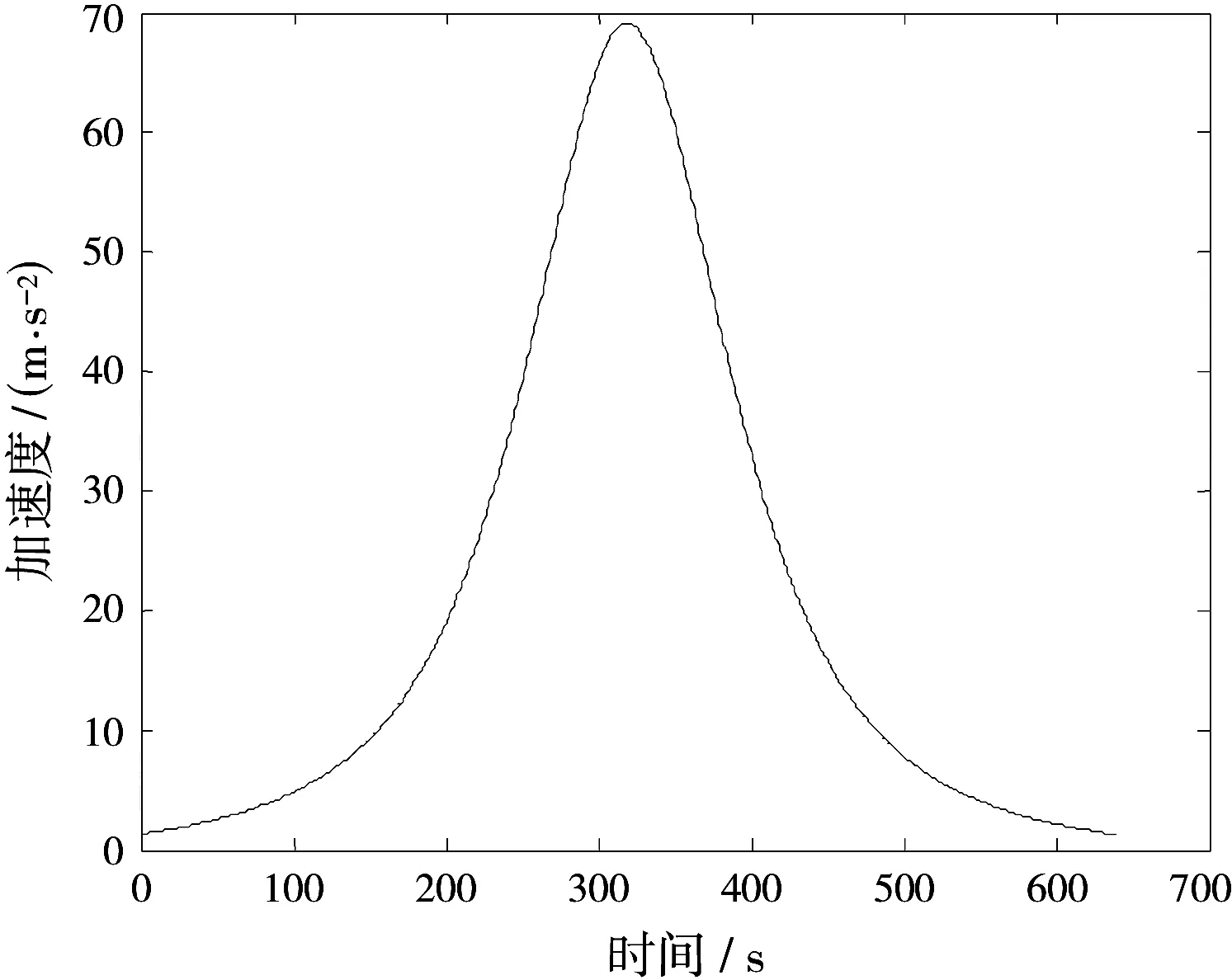
图4 ISS某次穿越雷达视场径向加速度时间关系

1.2 双基地雷达回波信号模型

假设雷达发射Chirp脉冲信号[7],其数学表达式为

式中,Tp为信号脉宽;b=B/Tp为调频率,B为信号脉冲带宽。

接收站收到的基带回波信号可以表示为

式中,fc为载频;t为快时间;t m=m Tr为慢时间,Tr为脉冲重复频率;tr=R(t m)/c为回波相对直达波的延迟时间,其中R(t m)为目标回波相对于直达波的路程差。

式(7)的傅里叶变换近似为

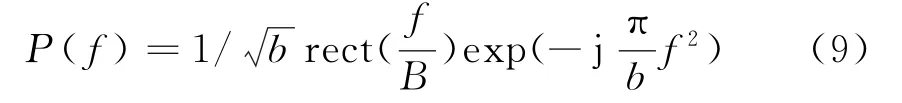
则式(8)的快时间傅里叶变换为

利用脉压函数对上式作匹配滤波,结果为

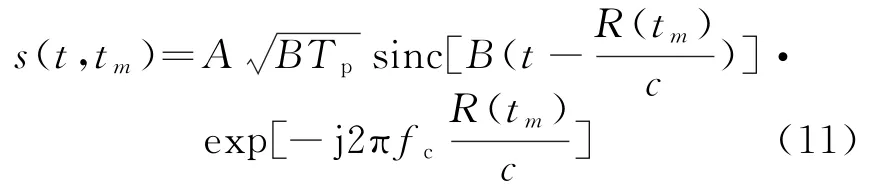
对于双基地雷达,R(t m)+RT(t m)+RR(t m)-L,RT(t m)代表目标与发射站的距离,RR(t m)代表目标与接收站的距离,L代表基线距离。

阶段一中目标相对于发射站或接收站在径向均维持匀速直线运动状态,则有

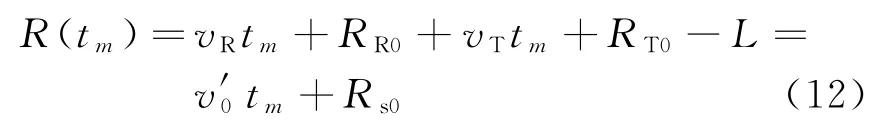
式中,Rs0=RT0+RR0-L,v′0=vT+vR,RT0和vT、RR0和vR分别表示目标相对于发射站、接收站的径向初始距离和初始速度。则回波包络峰值时刻[8]为

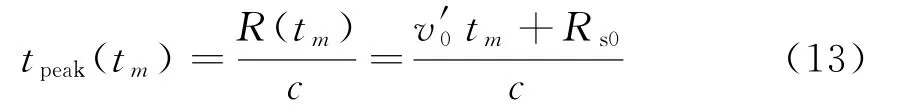
从式(13)可以看出,基带回波匹配滤波后包络峰值位置随慢时间变化而变化。若在积累时间内包络移动超过一个距离单元便产生了跨距离单元走动。

同理,当目标处于阶段二时有

a′0=aT+aR,其中aT,aR分别表示目标相对于发射站和接收站的径向初始加速度。可见此时R(t m)是t m的二次函数,同样可能在积累时间内出现跨距离单元走动的问题。

2 空间目标积累检测算法

本文充分利用空间目标不同阶段在运动状态和回波信噪比等方面各自的特点,寻找能够有效实现目标检测的方法,并通过Matlab仿真实验对其检测性能进行分析。

2.1 空间目标大斜距时积累检测算法

当目标斜距最大时对应1.1节中的阶段一,此时目标离接收站最远,回波信噪比较低,并且对于双基地雷达来说天线增益较小,不足以达到检测概率的要求,因此需要通过多条回波的能量积累以实现目标检测。

阶段一中目标在径向维持匀速直线运动状态,将表达式R(t m)=Rs0+v′0t m代入式(10),得

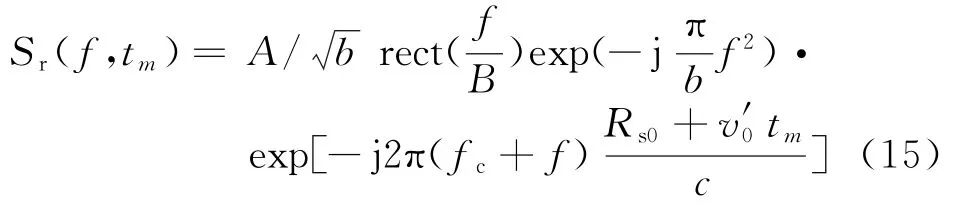
由式(11)、(13)和(15)可知,造成距离走动的因子为。若对上式乘以与目标的初始速度一致的速度补偿因子便可得到

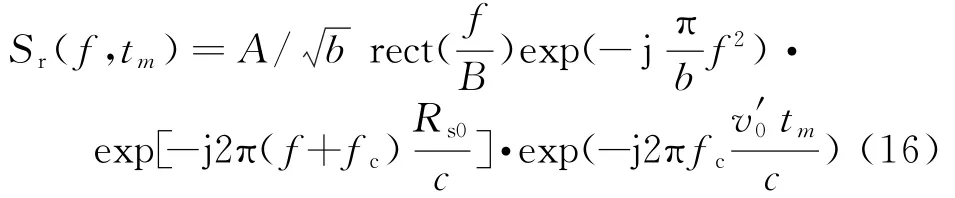
对上式作匹配滤波得

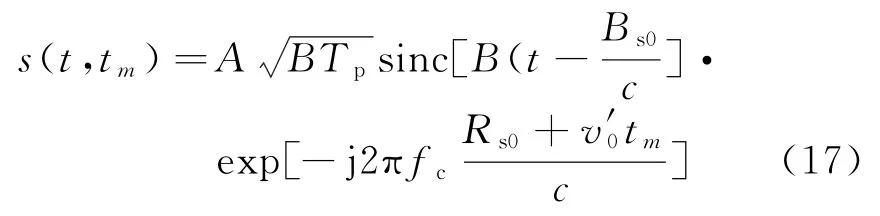
从上述分析可见只要补偿的速度值跟初始运动参数吻合便能解决跨距离单元走动问题,实现回波包络对齐。针对距离走动问题,文献[9-10]使用了包络插值移位算法对距离走动进行补偿,但必须以事先精确估计目标运动速度为前提,这对于目标检测来说并不是实现已知的。

本文采用两级速度补偿算法对阶段一中空间目标进行积累检测。信号处理流程见图6中速度补偿部分。具体步骤如下：

① 根据轨迹预报可以确定目标在阶段一时的速度区间为 [Vmin,Vmax]。采用大步长δv1将速度区间划分成M1个速度通道。

②将各速度通道值v i代入速度补偿因子中,并与回波信号相乘,实现速度粗补偿。

③ 对M1个速度通道补偿后的快时间频域-慢时间域信号Sr(f,t m)分别作慢时间傅里叶变换。根据有无目标时的多次仿真实验设定经验阈值T1,若最大积累峰值超过T1,则将峰值最大处对应的速度通道V1作为v′0的粗估计。

④ 再用小步长δv2将速度区间[V1-δv1,V1+δv1]划分成M2个子通道,重复步骤②和③,若最大峰值超过T2,其对应的速度通道值V2便是对v′0的精确估计,同时峰值处对应的距离便是初始距离参数Rs0。

⑤ 利用Rs0和接收站测得的方位角根据余弦定理可以计算出该帧起始时刻的RT0和RR0,vR和vT。

2.2 空间目标小斜距时积累检测算法

当目标距离雷达接收站最近时对应1.1节中的阶段二。通过对1.1节的分析可得此阶段的两个特点：(1)距离接收站最近,因此接收到的回波信噪比在全过程中最高;(2)目标径向速度最小,所以一定积累时间内跨距离走动在全过程中最小。

非相参积累的工程实现比较简单,且对雷达收发系统没有严格的相参性要求。针对阶段二中的目标,在积累时间内回波间不满足严格的相参性条件。若此时缩短积累时间进行传统非相参积累会进一步减小距离走动,同时本身回波信噪比较大,只要积累时间选取合理通过非相参积累能够较好地实现目标检测。对于雷达非相参积累技术,不论是基于动态规划、还是Hough变换,抑或粒子滤波,其算法流程相对复杂,计算量较大,不适用于阶段二高信噪比和低速的条件。

在充分利用阶段二中目标回波及运动特点和统筹系统工程实现的基础之上,本文采用传统的非相参积累算法就能够使该阶段的目标回波能量得到有效积累,简单便捷地实现目标检测。

2.3 空间目标中间时段积累检测算法

当目标斜距位于中间段时,对应第1.1节中的阶段三。根据之前的分析,阶段三中目标短时间内在径向近似为匀速直线运动,因此减少积累脉冲个数可以保证在积累时间内目标速度保持不变。选取连续发射的M条脉冲作为一帧,M的取值应使帧内目标速度的变化可忽略。帧与帧之间间隔10s,用以拉开各帧之间的速度差异。帧划分原理图如图5所示。在帧划分后将相参积累运用于帧内,通过时间关联最终重现目标运动轨迹。

阶段三的信号处理方法具体如下：首先,选取合适的帧划分参数M和M′,将阶段三分成多帧。然后,对于每帧M条脉冲按照2.1节中的两级速度补偿方法通过相参积累估计出每帧起始时刻目标相对于接收站的距离RR0和速度vR。最后,重现目标在阶段三的点迹图,并将积累所得点迹图与轨迹预报作比较,评价算法的优劣。帧划分原理图以及阶段三整个信号处理流程如图6所示。

图5 帧的划分原理图

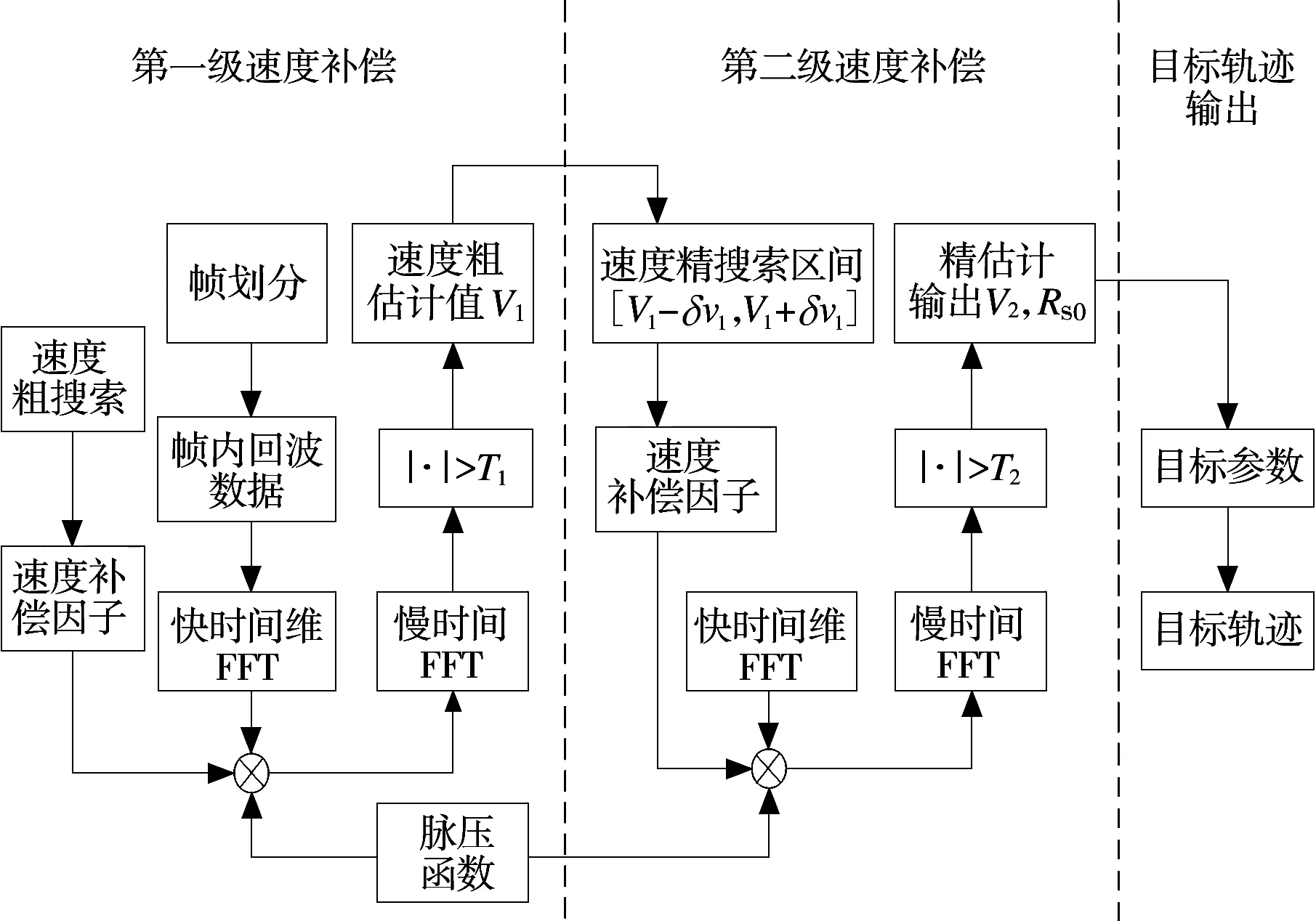
图6 阶段三信号处理流程图

3 仿真实验

实验一：以ISS某次预报中斜距最大时的运动参数作为目标仿真参数用来产生模拟回波,并加入复高斯白噪声,速度精、粗搜索步长分别为1 m/s和100 m/s,整体参数设置见表1。图7为无噪声时匹配滤波的结果,图8为信噪比为-30 dB时匹配滤波结果。图9为两级速度补偿后距离多普勒三维图,不补偿距离走动直接积累的结果见图10。由图7可知回波间出现了跨距离单元走动现象。图8和图10中回波所包含的有用信号完全被噪声淹没,已无法检测出目标的位置。通过本文算法对速度进行补偿后目标的能量得到了积累,其峰值明显高于周围的噪声,使目标能够被检测出来。从仿真结果可以看出两级速度补偿算法能够较好地补偿大斜距时的距离走动。

表1 实验一仿真参数

图7 无噪声时匹配滤波结果

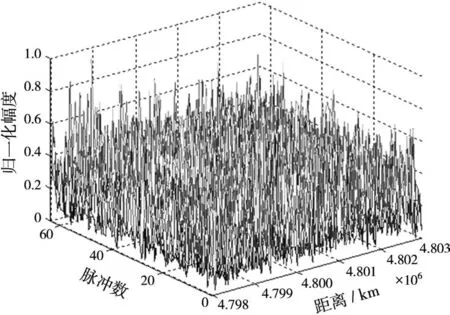
图8 SNR=-30 dB时匹配滤波结果

图9 SNR=-30 dB时本文所用算法结果

图10 SNR=-30 dB时直接积累结果

为了进一步验证该算法的有效性,在虚警概率为10-6时,通过103次 Monte Carlo实验统计出输入信噪比和目标检测概率的关系曲线[11-13],如图11所示。为了增强实验的对比性,将文献[10]中包络插值移位算法和直接积累算法作为对照组进行对比。

图11可以得出当检测概率为0.5时,本文算法需要的SNR比文献[10]算法需要的SNR低2.5 dB左右。

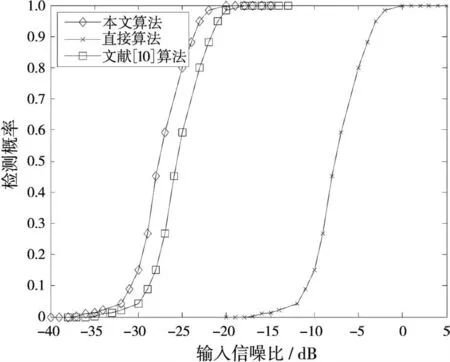
图11 检测性能曲线比较图

实验二：将实验一同次的ISS预报中斜距最小时的运动参数作为目标仿真数据,整体参数设置见表2。此时ISS相对接收站径向速度从100～2 000 m/s匀加速渐变。在信噪比固定为-15 d B,径向初始速度选取500 m/s、1 500 m/s的条件下,进行两组仿真实验,结果见图12、图13。可见此时使用非相参方法对回波能量进行积累能简单有效地检测出目标的位置。比较两幅图发现目标初始速度越大非相参积累的效果越差,但因此时目标回波高信噪比的特点使得非相参积累成为在保持一定检测概率的情况下,检测目标工程实现最简单的途径。

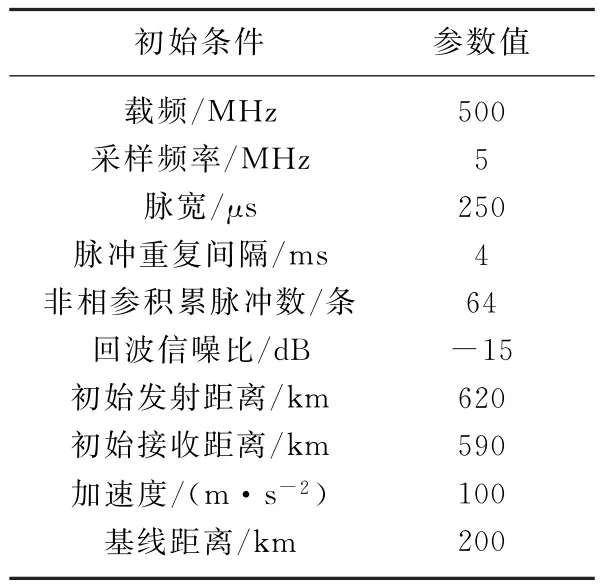
表2 实验二仿真参数

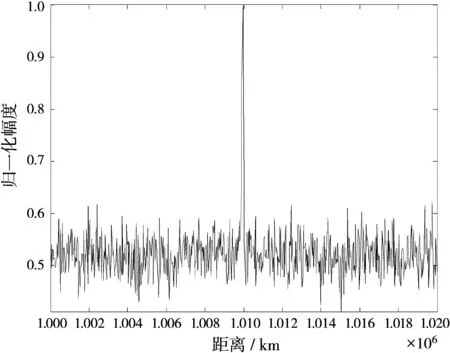
图12 SNR=-15 dB,v0=500 m/s时非相参积累结果

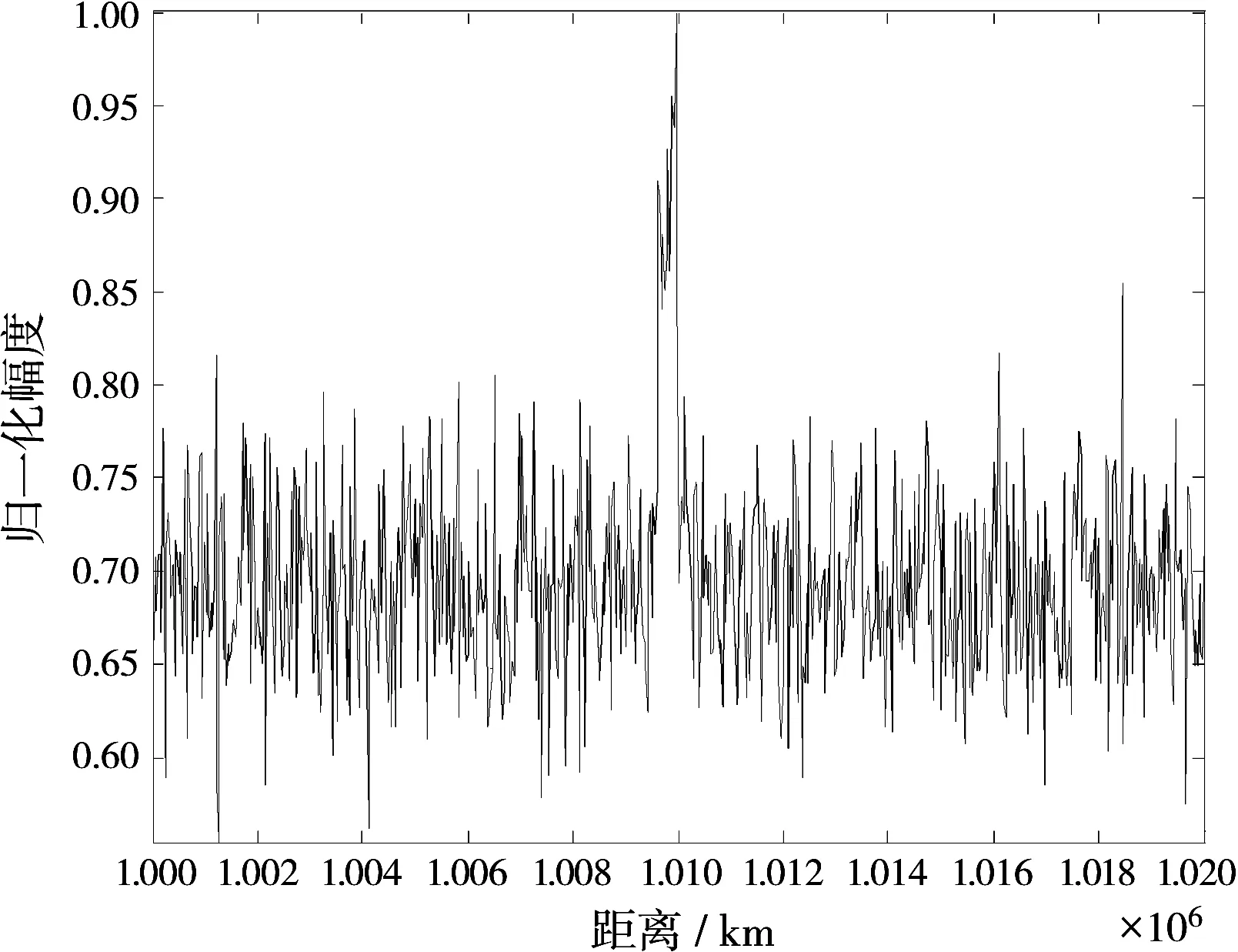
图13 SNR=-15 dB,v0=1500 m/s时非相参积累结果

实验三：系统仿真参数设置同实验一。选取帧头积累脉冲数M=64,则根据轨迹预报信息计算出ISS每次穿越雷达视场时的阶段三可划分为20～30帧。利用与实验一同次的ISS轨迹预报中阶段三每帧起始时刻的速度和位置信息设置目标仿真参数。按照2.3节中的分析,对阶段三的各帧分别进行积累检测,便可得到目标相对接收站的轨迹图。为验证参数估计精度,通过103次Monte Carlo实验统计不同信噪比时的距离和速度估计误差,如图14、图15所示。直接补偿算法对于高速运动的目标而言,积累增益很低,发现目标已很困难,参数估计误差很大,此处不予画出。文献[10]算法在速度已知的情况下才能实现参数估计,且参数估计误差比本文算法要高。可见本文算法能够对空间目标运动参数实现较好的估计,同时对噪声具有一定的鲁棒性。

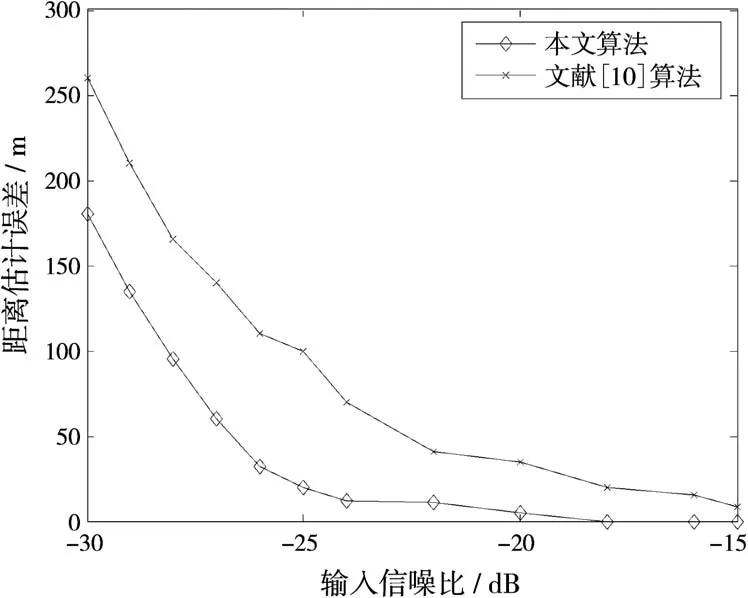
图14 距离估计精度比较

图15 速度估计精度比较

本文以空间目标的代表ISS为例来进行仿真实验,其轨道高度约为380 km,属于低轨道空间目标之一。对于其他空间目标,根据实际情况合理调整积累检测时的速度搜索范围,积累时间等一系列参数,按照本文算法也能较好地实现目标检测。

4 结束语

本文将空间目标经过双基地雷达视场的运动过程分成三个阶段,在充分研究每个阶段目标运动规律和回波特性的基础上,选用两级速度补偿算法解决阶段一和阶段三中的跨距离单元走动问题,并通过仿真实验对比验证了该算法的有效性。利用阶段二回波高信噪比的特点,选择传统非相参积累算法直接对阶段二中的回波能量进行积累。从而在总体上实现空间目标穿越雷达视场全过程的目标检测。

[1]刘林.航天器轨道理论[M].北京：国防工业出版社,2000：189-217.

[2]张光斌.双/多基地雷达参数估计算法研究[D].西安：西安电子科技大学,2006.

[3]XING Mengdao,SU Junhai,WANG Genyuan,et al.New Parameter Estimation and Detection Algorithm for High Speed Small Target[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(1)：214-224.

[4]XU J,YU J,PENG Y N,et al.Radon-Fourier Transform for Radar Target Detection,I：Generalized Doppler Filter Bank[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(2)：1186-1202.

[5]ALI I,AI-DHAHIR N,HERSHEY J E.Doppler Characterization for LEO Satellites[J].IEEE Trans on Communications,1998,46(3)：309-313.

[6]袁振涛.空间目标普测型雷达信号检测与参数估计算法研究[D].长沙：国防科学技术大学,2009.

[7]SU J,XING M,WANG G,et al.High-Speed Multi-Target Detection with Narrowband Radar[J].IET Radar,Sonar and Navigation,2010,4(4)：595-603.

[8]蒋千,孔令讲,杨建宇.一种径向匀加速目标包络徙动补偿新方法[J].雷达科学与技术,2013,11(1)：45-50.JIANG Qian,KONG Ling-jiang,YANG Jian-yu.A New Method for Envelope Migration Correction of Target with Radial Acceleration[J].Radar Science and Technology,2013,11(1)：45-50.(in Chinese)

[9]陈远征,朱永锋,赵宏钟,等.基于包络插值移位补偿的高速运动目标的积累检测算法研究[J].信号处理,2004,20(4)：387-390.

[10]夏卓卿,陆军,陈伟建.一种Chirp雷达包络对齐新方法[J].雷达科学与技术,2010,8(1)：44-48.

[11]何友,关键,孟祥伟,等.雷达目标检测与恒虚警处理(第2版)[M].北京：清华大学出版社,2011.

[12]BANDIERA F,DE MAIO A,RICCI G.Adaptive CFAR Radar Detection with Conic Rejection[J].IEEE Trans on Signal Processing,2007,55(6)：2533-2541.

[13]CHEN J J,QIU W,HUANG M J,et al.A Novel CFAR Detector for Terminal Guidance Coherent Radar[C]∥Proceedings of the Internationa Conference on Signal Processing Systems,Beijing,China：[s.n.],2010：2253-2256.