基于模糊贴近度和非紧凑邻域的变化检测

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

变化检测是通过分析同一地区不同时刻获取的图像来识别一个目标或者现象的状态差异的过程[1]。近年来,由于SAR图像相比光学图像具有不受气候和太阳光照条件影响的特点,越来越多的学者通过分析SAR图像来识别相关的变化。虽然SAR图像数据的内在复杂性,既要求一个有效的降斑预处理,又要求一个有效的能处理该斑点噪声的分析技术,使得通过SAR图像识别变化区域的难度有所增加,但仍有大量的相关技术形成,并用于地震灾区的标识[2]、水灾监控[3]和栽种面积的评估[4]等方面。

一般地,SAR图像变化检测由预处理、差异图构造和变化检测结果生成[5]三步完成。预处理主要是对原始两时相SAR图像进行诸如匹配、辐射校正、几何校正和噪声去除等处理。对已配准、已校正的两时相SAR图像,预处理的主要目的是降低斑点噪声。现有变化检测方法大多采用Lee或Gamma MAP等滤波器进行降斑。差异图构造则是为生成可后续处理的特征图,常用的方法有比值法、对数比值法和区域均值法等。变化检测结果生成,根据其所利用的信息,可分为上下文不敏感和上下文敏感两大类。上下文不敏感方法只利用像素自身的信息,如文献[5]方法,通过假设类统计分布模型和推导出相应的阈值选择标准,阈值分割差异图生成变化检测结果。上下文敏感方法利用像素的一个邻域内信息。由于上下文敏感方法考虑了相邻像素间具有的相关性,其变化检测性能通常优于上下文不敏感方法,诸如通过马尔可夫模型(MRF,Markov random field)模型[6]、Hopfield神经网络(HNN,Hopfield neural network)以能量的形式将空间关系引入变化检测结果生成阶段。结果显示,由于邻域像素信息的利用,变化检测性能都有所提高,但该邻域的大小和形状都被固定,导致变化检测方法对几何细节不敏感,造成变化区域的边缘有过光滑现象。

为提高变化检测性能和改善变化检测效果,本文提出一种新的差异图构造方法,并基于主动轮廓模型分割技术完成了两时相SAR图像的水灾变化检测。所提方法避免了上下文不敏感技术[5-6]的变化检测性能受影响于统计分布模型的合理性的缺陷,突破了上下文敏感技术只利用固定形状和大小邻域内像素信息的限制。本文方法因无需假设统计分布模型和能利用非紧凑邻域内像素信息对当前像素进行决策,其变化检测性能优于其他相关算法。两组真实SAR图像数据的变化检测结果,验证了本文方法的有效性。

1 差异图构造及变化检测结果生成

1.1 模糊贴近度差异图

模糊贴近度原本为度量两个模糊子集间相似性测度。Weken等人[7]成功将其应用于图像比较,并为改善效果,将基于像素的相似性测度推广到基于邻域的相似性测度。贴近度度量公式的形式有多种,但本文选用如式(1)相似性度量公式构造差异图,是在于其采用的比值形式和能利用窗口内像素信息增强差异图的类内一致性,这有利于克服SAR图像的乘性斑点噪声和后续变化检测结果生成。

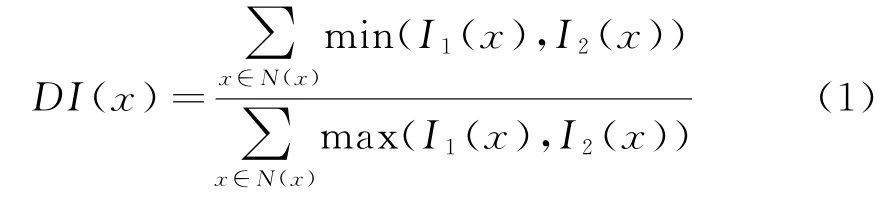
考虑到窗口在降低斑点噪声和保持细节信息方面的两难兼顾,对已配准、已校正的两时相SAR图像I1和I2,选取3×3的窗口N(x)构造差异图DI,其中N(x)为与x在位置上相邻的位置元素构成的集合,诸如二阶邻域。对位置x上的像素,取其空间上的一个邻域,把由邻域元素构成的集合看作是模糊向量,用式(1)度量两模糊向量间的相似度。式(1)值越大,位置x上的对应像素间的相似度越高,则该点属于非变化类的可能性更大;反之,该点属于变化类的可能性更大。为方便后面陈述,将依据相似度公式构造的差异图称为模糊贴近度差异图。

1.2 变化检测结果生成

主动轮廓模型是一种基于能量的分割方法,其基本思想是进化一条或多条受限于给定图像的曲线,使之向目标的边缘逐渐靠近,以达到分割的目的。对已配准、已校正的SAR图像构造差异图DI后,本文以主动轮廓模型为原型的分割技术对差异图分析生成变化检测图,即把差异图分成两类：变化类wc和非变化类wn。若把DI∶Ω→R看成一个包含两区域的连续的标量场,并用Ω表示其图像域,C0表示DI中两类的边界曲线,即wc的边缘;则对在图像域Ω中的任意一条封闭曲线C,我们希望曲线C进化到边界曲线C0时停止,此时曲线C包围的区域对应wc,C之外而Ω内的区域对应wn,也就完成了变化检测。

以主动轮廓模型为原型的分割技术,其本质为把分割的问题映射为能量的问题,通过求能量的最小化问题完成图像分割,能量表达式为

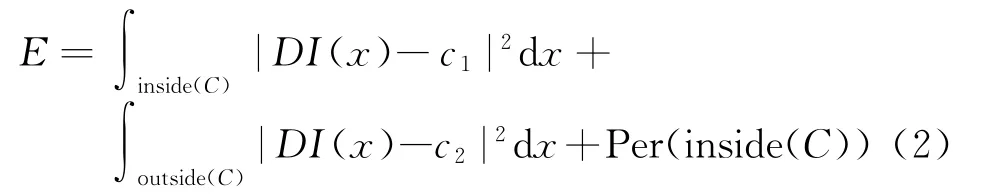
式中,C为任意假设的在Ω中的封闭曲线,若假设C为Ω中一个真子集w的边界(即w⊂Ω,C=∂w),则inside(C)为区域w,outside(C)为区域Ω/¯w;Per(inside(C))是给曲线C施加光滑约束的正则项;c1和c2是依赖于C的常数,其中c1表示曲线C包含的像素灰度均值,c2表示落在曲线C外像素的灰度均值。不难看出,当C收缩在wc的边缘C0时,式(2)达到最小值,即以主动轮廓模型为原型的分割技术对差异图分析的问题转化为求式(2)最小值的问题。

直接求解式(2)的最小值存在易陷于局部最小值的缺点,因此利用加权的总差分范数(TV,total variation)将经典的主动轮廓模型和无边界的主动轮廓模型(ACWE,active contour without edges)模型结合,变换如式(2)所示的能量函数为

式中,r(x,c1,c2)=(c1-DI(x))2-(c2-DI(x))2;表示以经典主动轮廓模型中的边缘指示函数g为权重的总差分范数。

求解如式(3)所示的能量表达式的最小值时,能确保收敛到全局最小,但仍存在收敛速度比较慢的问题。为此,用对偶规划将式(3)变为式(4)[8]：

式中,参数θ为大于零的小数值。求解如式(4)表示的能量最小化问题时,已有的数值实现能确保较快的收敛到全局最小;该策略通过迭代的解决如下两个能量最小值问题：

(1)固定v不变,求u

(2)固定u不变,求v

来求如式(4)表示的能量最小化问题,而式(5)的解为

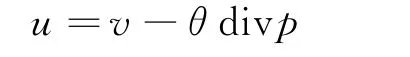
式(6)的解为

更多的信息可参见文献[8]。一定的迭代次数完成后,u即为所求的变化检测结果。从函数形式转变的整个过程来看,如式(4)所示的能量形式使曲线的进化趋势由经典主动轮廓模型中的指示函数g与被ACWE模型利用的区域同质性特点共同决定,以致即使差异图中两类的对比度不高,该模型也能使曲线逐渐进化收敛于变化区域的边缘轮廓。

为使模糊贴近度差异图近似满足分片恒值(piecewise-constant)的条件,可先采用双边滤波器处理模糊贴近度差异图。

2 实验分析

为了证明本文方法的有效性,我们分别证明了如下两个方面：(1)差异图构造方法的有效性;(2)变化检测性能改善的有效性。为定量地比较变化检测效果,依据参考图,给出了不同变化检测结果的漏检数(变化的像素被判为未变化的像素个数)、虚警(未变化的像素被判为变化的像素个数)、总错误检测数(漏检数+虚警数)和Kappa系数等四个性能评价指标,

式中,N为差异图像素单元总数,E c为变化区域内像素单元被正确检测的个数,T c为非变化区域内像素单元被正确检测的个数。漏检及虚警的像素单元个数越少,Kappa系数越大,变化检测性能越好。

2.1 实验数据描述

图1给出了用于验证变化检测性能的第一组真实SAR图像数据集。该数据集由ERS-2分别于1999年4月和5月获取的瑞士Bern城市水灾发生前后两时相SAR影像构成。图1(a)为洪水发生前SAR影像,图1(b)为受水灾后SAR影像。SAR影像尺寸均为301×301。图1(c)为实际变化参考图,图中的白色像素表示两时相间发生变化的区域,像素个数为1 155。

图1 Bern实验数据

第二组真实的SAR图像数据集原始图像及参考变化图如图2所示。其中数据集的原始图像分别为加拿大Ottawa地区的1997年5月和1997年8月Radarsat SAR影像,如图2(a)和(b)所示。两幅图像的大小均为350×290,灰度级为256,配准误差为1.5个像素左右。前后时相的变化在于雨季(5月)期间部分陆地区域被淹没。图2(c)为参考变化检测图,图中的白色像素表示两时相间发生变化的区域,像素个数为16 049。

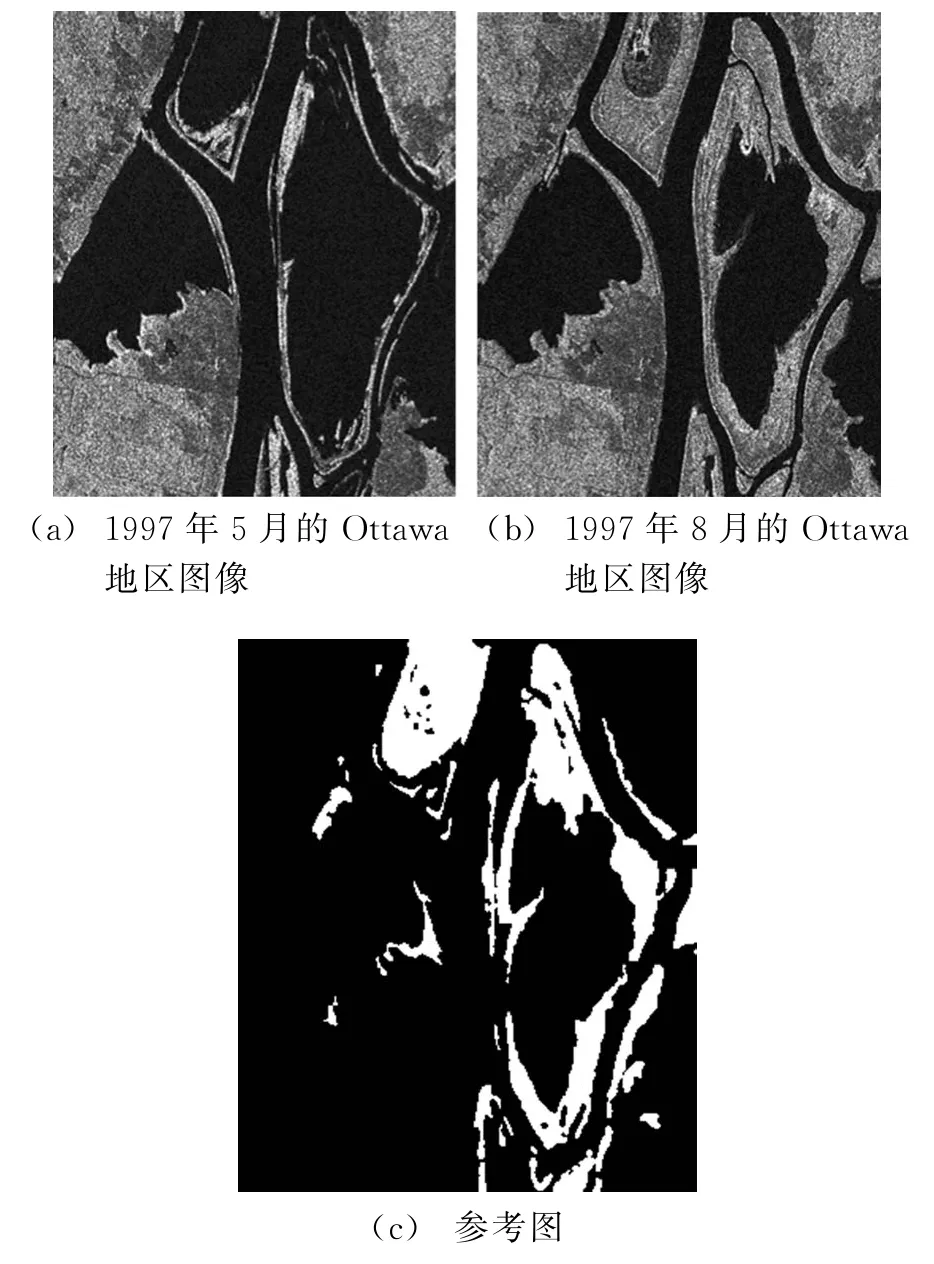
图2 Ottawa实验数据

2.2 差异图构造方法有效性验证

依据参考图,采用一种有监督的方式,计算差异图中变化类和未变化类的方差。方差越小,类内一致性越好。图3展示了比值法、对数比值法及区域均值比值法等经典构造方法的差异图以及本文的模糊贴近度差异图,其中构造区域均值比法差异图时,同样采用3×3的窗口。从效果图上看,比值法差异图的变化区域很明显,但未变化区域存在易产生错误检测数的像素,因其灰度值与变化区域内像素相当;对数比值法差异图的未变化区域的一致性较好,但是变化区域信息有所丢失,易造成变化区域像素单元的漏检较多;区域均值比差异图,相比于本文差异图,变化类与非变化类的对比度较强,但未变化类的一致性略差于本文差异图。

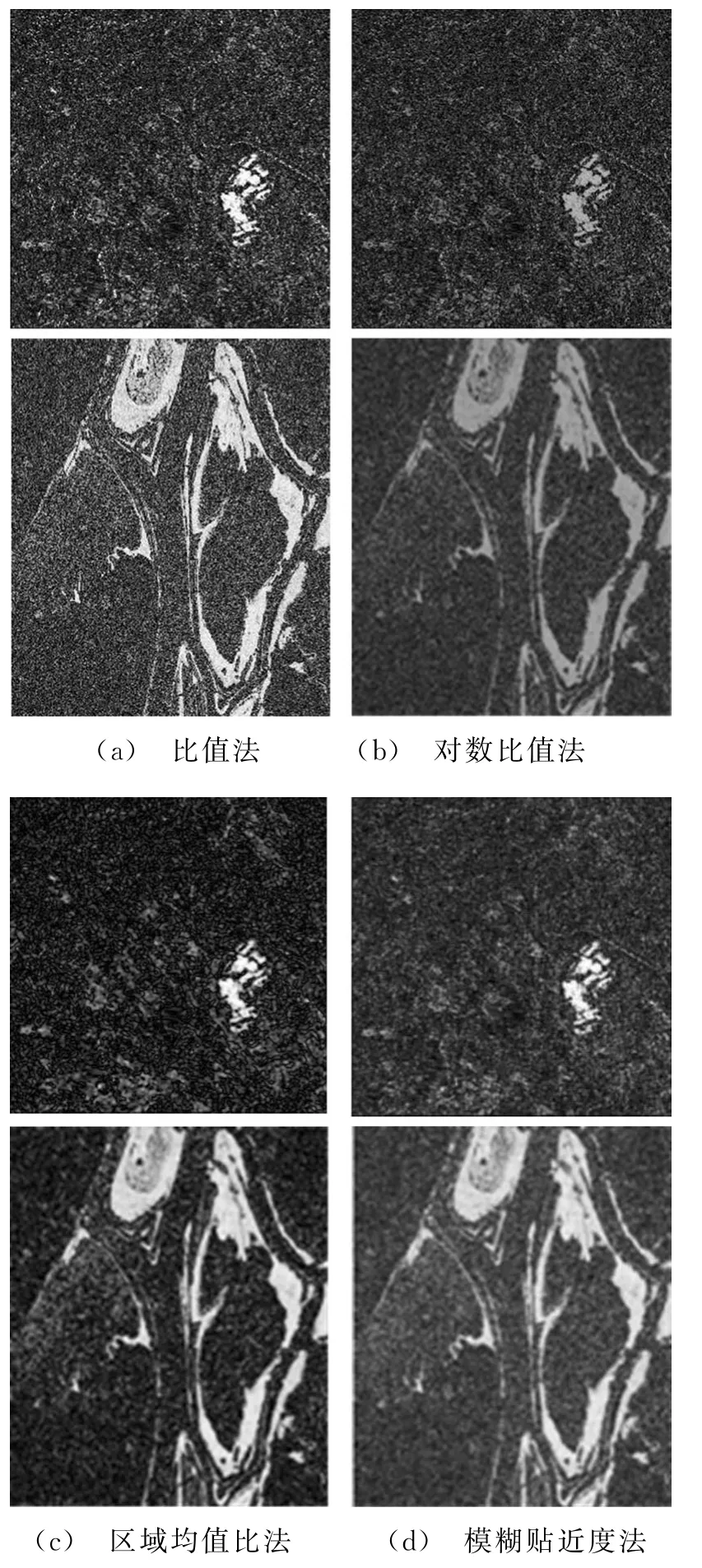
图3 两组实验数据各方法构造的差异图

表1 两组实验数据差异图中两类的方差

分析表1数据可知：对Bern实验数据,本文方法构造的差异图,变化类和未变化类的方差均优于经典方法构造的差异图;对Ottawa实验数据的结果亦如此。这从定量的角度验证了本文模糊贴近度差异图构造方法的有效性。

2.3 变化检测性能改善有效性验证

本文所提变化检测方法具有不涉及统计分布模型假设和上下文敏感两个特点。为了验证不涉及统计分布模型假设的有效性,给出了涉及统计分布模型变化检测方法的检测结果图,为陈述方便,假设类分布符合高斯模型的分析技术记为GKIT,假设类分布为广义高斯模型的分析技术记为GGKIT;假设类分布符合对数正态分布的分析技术记为LN-GKIT;假设类分布符合“Weibull-Ratio”模型的分析技术记为 WR-GKIT。为了体现本文方法利用上下文信息对检测效果的贡献,给出了两种已有上下文敏感变化检测方法的结果,分别记为EM+MRF,HNN。

图4给出了Bern实验数据集的变化检测结果;图5给出了Ottawa实验数据集的变化检测结果。表2给出了对应的定量分析评价指标。

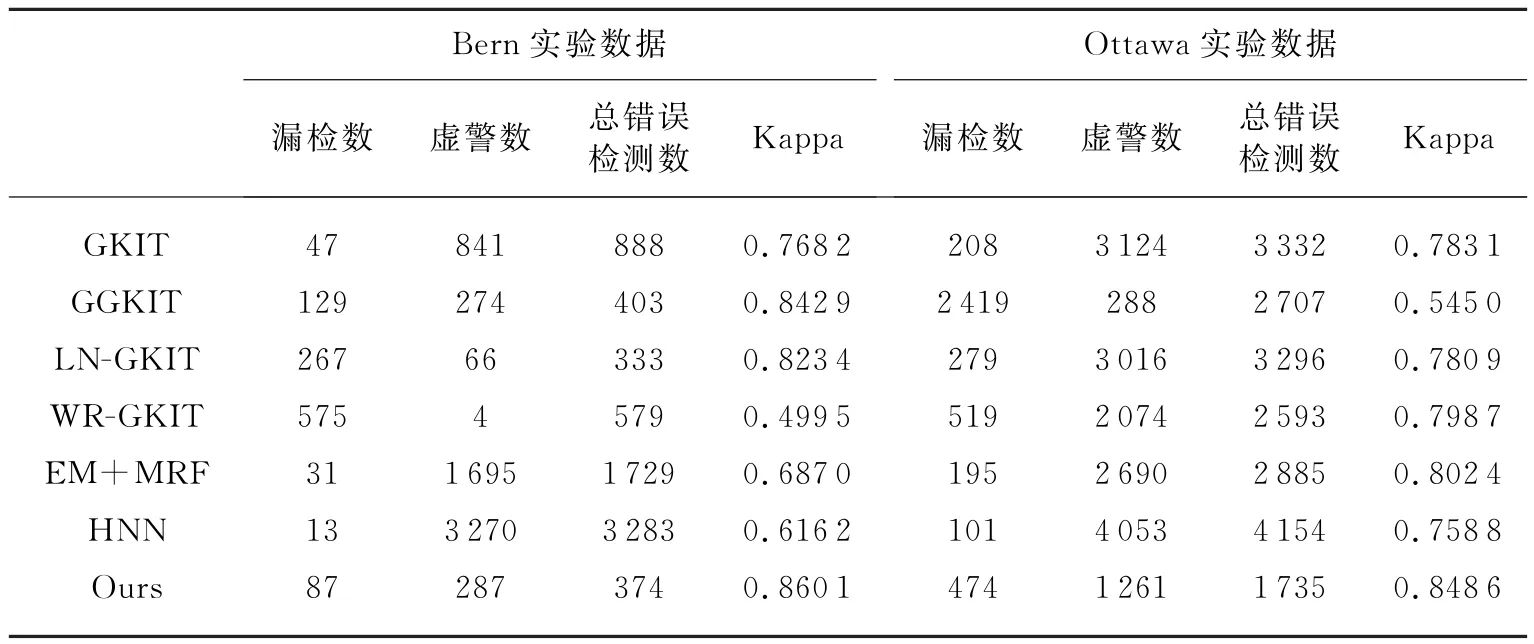
表2 两组实验数据变化检测结果的定量分析指标

图4 Bern实验数据变化检测结果

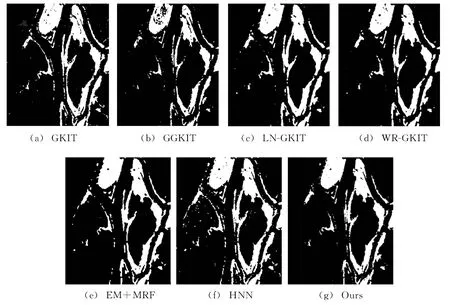
图5 Ottawa实验数据变化检测结果

分析表2的数据,本文所提变化检测方法对两组实验数据变化检测结果的Kappa系数都最高。对Bern实验数据,本文方法的Kappa系数比GGKIT法高0.0172,比LN-GKIT方法高0.0367,比EM+MRF法高0.1731,比HNN法高0.2439;对Ottawa实验数据,本文方法的Kappa系数比GKIT法高0.063,比 WR-GKIT法高0.064 1,比EM+MRF法高0.046 2,比HNN法高0.089 8。这是因为本文方法避免了类统计分布选择的合理性对检测结果的影响,同时,通过非紧凑邻域像素的信息增强了对几何细节信息的敏感性。

两组实验数据的分析,从定量的角度验证了本文方法的有效性。从定性的角度看,本文方法检测的变化区域的边缘更接近于真实变化区域的轮廓。

3 结束语

基于模糊数学概念,本文构造了一种新的差异图,并基于主动轮廓模型,突破了只利用固定形状和大小邻域内像素信息的限制,利用了非紧凑局部邻域内的像素信息,形成一种非紧凑邻域的上下文敏感变化检测方法。真实SAR图像数据的变化检测结果表明,本文所提变化检测方法既提高了变化检测性能,又改善了视觉效果。

[1]王刚,刘智,王番,等.基于KL距离的SAR影像变化检测[J].雷达科学与技术,2012,10(1)：59-63.WANG Gang,LIU Zhi,WANG Fan,et al.A Change Detection Method of SAR Image Based on Kullback Leibler Divergence and Morohology[J].Radar Science and Technology,2012,10(1)：59-63.(in Chinese)

[2]BRETT P T B,GUIDA R.Earthquake Damage Detection in Urban Areas Using Curvilinear Features[J].IEEE Trans on Geoscience and Remote Sensing,2013,51(9)：4877-4884.

[3]GIUSTARINI L,HOSTACHE R.A Change Detection Approach to Flood Mapping in Urban Areas Using TerraSAR-X[J].IEEE Trans on Geoscience and Remote Sensing,2013,51(4)：2417-2430.

[4]SAKAMOTO T,WARDLOW B D,GITELSON A A.Detecting Spatiotemporal Changes of Corn Development Stages in the U.S.Corn Belt Using MODIS WDKVI Data[J].IEEE Trans on Geoscience and Remote Sensing,2011,49(6)：1926-1936.

[5]MOSER G,SERPICO S B.Generalized Minimum-Error Thresholding for Unsupervised Change Detection from SAR Amplitude Imagery[J].IEEE Trans on Geoscience and Remote Sensing,2006,44(10)：2972-2983.

[6]BRUZZONE L,PRIETO D F.Automatic Analysis of the Difference Image for Unsupervised Change Detection[J].IEEE Trans on Geoscience and Remote Sensing,2000,38(3)：1171-1182.

[7]VAN DER WEKEN D,NACHTEGAEL M,KERRE E E.Using Similarity Measures and Homogeneity for the Comparision of Images[J].Image and Vision Computing,2004,22(9)：695-702.

[8]BRESSON X,ESEDOGLU S,VANDERGHEYNST P,et al.Fast Global Minimization of the Active Contour/Snake Model[J].Journal of Mathematical Imaging and Vision(JMIV),2007,28(2)：151-167.