两杆欠驱动机器人的多层嵌套滑模控制方法

韩秀英，郭爱芳

(河南科技大学机电工程学院，河南洛阳 471003)

两杆欠驱动机器人的多层嵌套滑模控制方法

韩秀英，郭爱芳

(河南科技大学机电工程学院，河南洛阳 471003)

目前对于两杆欠驱动机器人的滑模控制方法大多不能保证子滑模趋近各自滑模面的可达性和鲁棒性，表现为系统的稳定过度依赖参数的选取，控制运行拥塞，参数调整难度大，实现困难。为此提出一种多层嵌套滑模控制方法，以改善子滑模趋向各自滑模面的可达性、鲁棒性和快速性。进行了系统滑模面的可达性和稳定性分析，并就Pendubot和Acrobot两类欠驱动机器人进行了位置镇定控制数值仿真。仿真结果表明该方法能够使系统的控制参数调整保持一定的连续性，降低控制拥塞和参数调整难度，并有效地提高子滑模趋向各自滑模面的快速性和鲁棒性。

欠驱动系统;Pendubot;Acrobot;位置镇定控制;滑模控制

欠驱动系统是指系统的独立控制变量个数小于系统自由度个数的一类非线性系统，其例子很多，如空间机器人、水下机器人、移动机器人、无人自行车、倒立摆、桥式吊车等，同时在实际中某些系统由于驱动器的减少或损坏，整个系统也会变为欠驱动系统，其中人为主动地将驱动器减少，也会使整个系统体积减小、质量减轻、成本降低。因此欠驱动系统的控制研究具有重要意义。

包括Pendubot和Acrobot在内的两杆欠驱动机器人是人们较为关注的典型的欠驱动系统，其两个关节中一个是自由的，另一个是有电机驱动的。目前对于这两种欠驱动机器人的控制方法很多，总的来说主要包括智能控制方法［1］、能量控制方法［2－3，9］、无源性控制方法［4］、混杂控制方法［5－9］以及滑模控制方法［10－11］等，其中滑模控制是一种简单实用的控制方法，在其滑动模态上运动时对于系统不确定性和外界扰动具有完全的鲁棒性，因此滑模控制的研究对于欠驱动机械系统具有重要的实际价值，王伟等人［12］针对Pendubot提出了一种分层滑模控制方法，实现了对两个被控输出量的同时控制，有效避免了其它控制方法存在切换力矩大、稳定时间长等不足;姜文超等［11］提出了一种从中间变量出发构造滑模函数的方法，使得滑模控制器变得更为简单。然而目前的滑模控制方法大多不能保证子滑模趋近各自滑模面的可达性和鲁棒性，表现为系统稳定过度依赖参数的调整，很多情况下无法调整出合适的参数，控制拥塞无法运行，甚至发散，控制任务难以实现。

为此，提出了一种多层嵌套滑模控制方法，以提高子滑模趋向各自滑模面的可达性、鲁棒性和快速性。

1 两杆欠驱动机器人的动力学模型

图1为两杆欠驱动机器人，它在铅直平面内运动，其中图1(a)为第一关节驱动，第二关节自由的Pendubot机器人，图1(b)为第一关节自由，第二关节驱动的Acrobot机器人。

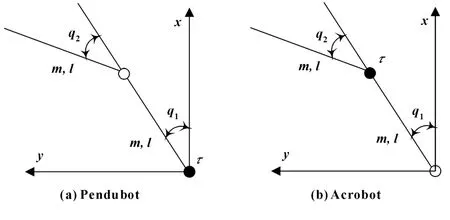
图1 两杆欠驱动机器人

如图1，q1，q2分别为机器人第一和第二关节的广义坐标。m，l分别为两杆的质量和杆长，这里假设两杆为等截面匀质杆。τ为驱动关节的驱动力矩。根据第二类拉格朗日方程，可得到两种机器人的动力学模型

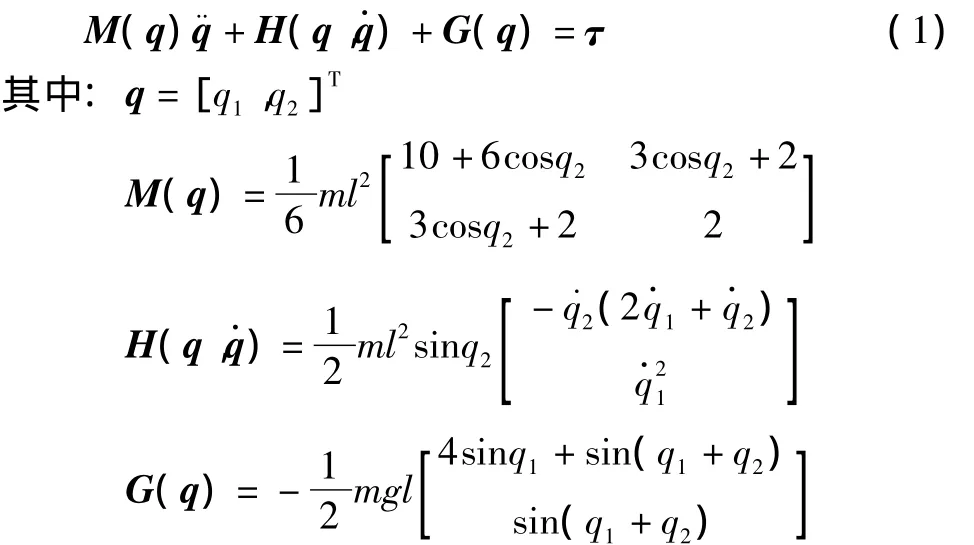
对于图1(a)和图1(b)所示的机器人，其驱动力分别为

模型(1)中惯性矩阵M(q)是对称正定矩阵，因此式(1)可写为

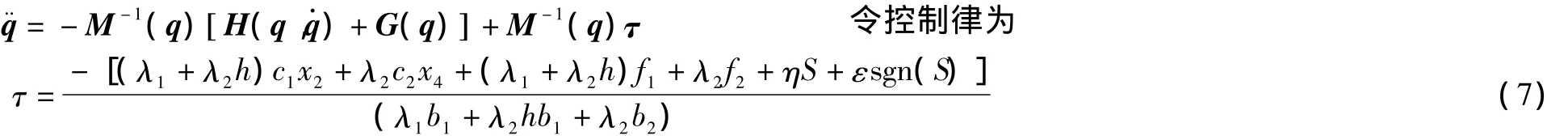
2 欠驱动机器人的多层嵌套滑模控制器

在铅直平面内运动的机器人有两个平衡状态，一个是机器人垂直指向上方，这种状态是不稳定状态，另一个是机器人垂直向下，这种状态是稳定状态。

在此，控制任务就是将机器人在有限时间内由垂直向下的稳定状态镇定到垂直向上的平衡状态。

这里首先构造两个子系统的滑模函数作为多层滑模函数的第一层

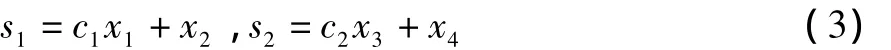
式中:c1＞0，c2＞0。

然后利用子滑模函数s1，s2构造第二层滑模函数

式中:h为常数。

最后再构造第三层滑模函数

式中:λ1为常数，λ2为正常数。

这样就实现了对滑模s1的嵌套，以利于避免集成控制造成的拥塞。

选取Lyapunov能量函数

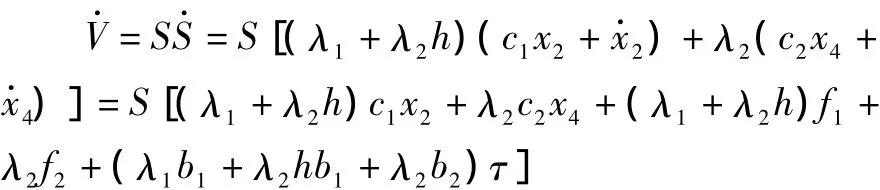
3 各层滑模面的可达性分析

定理1:对于系统(2)，采用式(3)—(5)所构造的滑动平面，如果选取控制律 (7)，则滑模面S满足可达性条件。

证明 系统(2)在控制律(7)作用下，由式(8)得，当S≠0时有

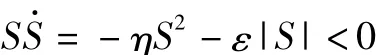
因此满足滑模面S的可达性条件。证毕。

定理2:对于系统(2)，采用式(3)—(5)所构造的滑动平面，如果选取控制律 (7)，且参数h的选取满足式 (9)，则在滑模S满足可达性条件的同时，子滑模s1，s2至少有一个满足可达性条件。

4 各层滑模面的稳定性分析

定理3:对于系统(2)，采用式(3)—(5)所构造的滑动平面，若采用控制律 (7)，则滑模面S是渐近稳定的。

定理4:对于系统(2)，采用式(3)—(5)所构造的滑动平面，如果选取控制律 (7)，且参数λ1的选取满足式 (11)，则子滑模面s1，s2也是渐近稳定的。

由式 (11)可知，当s1z≥0时，λ1=a，又λ2＞0，a＞0，因此可保证λ1λ2s1z≥0;当s1z＜0时，λ1=－a，因此可保证λ1λ2s1z≥0，从而保证了式(13)成立，即s1∈L2，s2∈L2成立。

(2)其次证明s1∈L∞，1∈L∞，s2∈L∞，2∈L∞。

5 仿真

欠驱动机器人的参数为m=3 kg，l=0.8 m。

首先以图1(a)所示的Pendubot机器人为控制对象，将其由垂直向下的静止初始状态 (q1=π，q2=0)镇定到垂直向上的状态 (q1=0，q2=0)，仿真结果如图2所示。

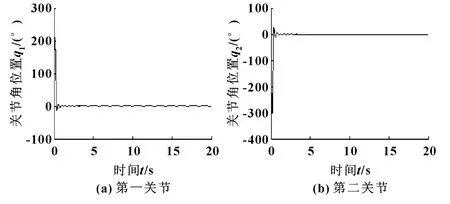
图2 Pendubot控制仿真

然后以图1(b)所示的Acrobot机器人为控制对象，将其由垂直向下的静止初始状态 (q1=π，q2= 0)镇定到垂直向上的状态 (q1=0，q2=0)，仿真结果如图3所示。

图3 Acrobot控制仿真

6 结论

针对目前的滑模控制方法大多不能保证所有滑模趋近各自滑模面的可达性和鲁棒性，控制运行容易拥塞，系统稳定难于调整的问题，提出了一种多层嵌套滑模控制方法，并进行了滑模可达性分析和稳定性分析。通过仿真表明，该方法能使系统的控制参数调整保持一定的连续性，降低调整难度，有效地提高所有滑模趋向各自滑模面的快速性和鲁棒性。

［1］BEGOVICH O，SANCHEZ E N，MALDONADO M.Takagi-Sugeno Fuzzy Scheme for Real-time Trajectory Tracking of an Underactuated Robot［J］.IEEE Trans on Control System Technology，2002，10(1):14－20.

［2］FANTONI I，LOZANO R，SPONG M W.Energy Control of the Pendubot［J］.IEEE Trans on Automatic Control，2000，45(4):725－729.

［3］李茂青.基于受控拉格朗日函数的Pendubot镇定控制器设计［J］.控制与决策，2010，25(5):663－668.

［4］SHIRIAEV A S，KOLESNICHENOKO O.On Passivity Based Control for Partial Stabilization of Underactuated Systems［C］∥Proc.of the 39thIEEE Conf.on Decision and Control.Sydney，Australia:IEEE Control Systems Society，2000:2174－2179.

［5］SPONG M W.The Swing Up Control Problem for the Acrobot［J］.IEEE Control Systems Magazine，1995，15(1):49－55.

［6］KAWADA K，FUJISAWA S，OBIKA M，et al.Creating Swing Up Patterns of an Acrobat Using Evolutionary Computation［C］∥Proc.of IEEE Inter-national Symposium on Computational Intelligence in Robotics and Automation.Kagawa，Japan:IEEE，2005:261－266.

［7］BERKEMEIER M D.FEARING R S.Tracking Fast Inverted Trajectories of the Underactuated Acrobot［J］.IEEE Trans on Robotics and Automation，1999，15(4):740－750.

［8］ZHANG M J，TARN T J.Hybrid Control of the Pendubot［J］.IEEE/ASME Trans on Mechatronics，2002，7(1):79－86.

［9］赖旭芝，吴敏，佘锦华，等.欠驱动两杆机器人的统一控制策略和全局稳定分析［J］.自动化学报，2008，34(1): 55－63.

［10］郑艳，朱媛，井元伟.一类欠驱动机械系统基于滑模的变结构控制［J］.东北大学学报:自然科学版，2005，26 (6):511－514.

［11］姜文超，戈新生.欠驱动Pendubot系统的滑模变结构控制［J］.北京机械工业学院学报，2008，23(1):5－8.

［12］王伟，易建强，赵冬斌，等.Pendubot的一种分层滑模控制方法［J］.控制理论与应用，2005，22(3):417－422.

Hierarchical Nested Sliding-mode Control of Under-actuated Two-link Manipulators

HAN Xiuying，GUO Aifang
(School of Mechatronics Engineering，Henan University of Science and Technology，Luoyang Henan 471003，China)

Currently，the greatest number of sliding-mode control means for the under-actuated two-link manipulators could not be assured of the reach-ability and robustness when all sub-sliding-modes approached one's own sliding-mode planes.It was appeared as stability of the system depended overly on selection of the parameters，and control running congested，and it was difficult to adjust the control parameters and implement.Therefore，a hierarchical nested sliding-mode control method was proposed to improve the reach-ability，robustness and rapidity.Both reach-ability and stability of all the sliding-mode planes were analyzed and numerical simulation of the position stabilization control of the pendubot and acrobot of the under-actuated two-link manipulators was done.The simulation results show that the control means can make adjustment of the control parameters keep more continuous，and decrease the control running congestion and difficulty of the parameters adjustment，and improve effectively the rapidity and robustness when all subsliding-modes approached one's sliding-mode planes.

Under-actuated systems;Pendubot;Acrobot;Position stabilization control;Sliding-mode control

TH112

A

1001－3881(2014)9－033－4

10.3969/j.issn.1001－3881.2014.09.009

2013－05－04

河南省教育厅基础研究重点项目 (13A460237)

韩秀英 (1971—)，女，学士，实验师，研究方向为机械系统测试及控制。E－mail:lhybxy@163.com。