基于小波去噪和最小二乘支持向量机的滚动轴承故障诊断研究

韩星，熊静琪，王李立，秦枭品

(电子科技大学机械电子工程学院，四川成都 611731)

基于小波去噪和最小二乘支持向量机的滚动轴承故障诊断研究

韩星，熊静琪，王李立，秦枭品

(电子科技大学机械电子工程学院，四川成都 611731)

针对滚动轴承故障，提出了基于相关原则优化阈值的小波去噪和最小二乘支持向量机相结合进行滚动轴承故障诊断的方法，采用相关原则优化阀值的小波对轴承早期故障特征进行提取，运用能量－特征法提取出信号特征，然后利用最小二乘支持向量机多分类算法进行故障类型的识别。实验与仿真结果表明:基于相关原则优化阈值的小波变换和最小二乘支持向量机相结合的故障诊断方法能有效地诊断出滚动轴承的典型故障。

滚动轴承;相关原则优化阈值;小波变换;最小二乘支持向量机;故障诊断

滚动轴承广泛应用于各种旋转机械中，其运行状态往往直接影响整机的性能。据统计，旋转机械的故障有30%是由轴承故障引起的，因此，滚动轴承的故障诊断显得尤为重要，而故障诊断中最重要、最关键的问题之一是故障特征参数的提取，它直接关系到滚动轴承故障诊断的准确性［1］。

Donoho［2］提出的小波阈值去噪法［3－4］，即软阈值去噪法、硬阈值去噪法，这两种降噪方法在早期得到了广泛的应用［5］。但Brace和Gao于1995年证明了硬阈值方法往往存在主要是由不连续造成的较大的方差，而软阈值方法往往存在主要由于对于大于阈值的系数做了收缩造成的较大的偏差。基于这些原因，目前人们已经提出了很多其他的改进方案［6－8］。

支持向量机 (Support Vector Machines，简称SVM)是基于统计学习理论的机器学习方法，采用的是结构风险最小化原则，能够较好地解决小样本、非线性、高维数和局部极小等实际问题，尤其能克服故障诊断中广泛存在的典型故障样本不足的问题［9］。最小二乘支持向量机 (Least Squares Support Vector Machine，简称LS-SVM)则改进了传统的SVM，采用二次损失函数，将SVM中的二次规划问题转化为线性方程组的求解，在保证精度的同时大大降低了计算复杂性［10］。同时，采用基于最小二乘支持向量机的故障分类算法，有效解决了滚动轴承样本数量过少以及效率低下的问题，且把支持向量机学习问题转化为线性方程组问题，在保证精度的同时大大降低了计算复杂性。

文中针对滚动轴承故障诊断，首先介绍一种改进的阈值去噪方法即基于相关原则优化阈值的小波去噪方法，证实了其相对于传统去噪方法的优点，然后将其应用于轴承故障信号的去噪，最后运用最小二乘支持向量机实现故障分类。通过相关原则优化阈值的db2小波对振动信号的局部特征进行信号分解，得到明显的故障特征频率信息，然后进行数据归一化，之后输入到LS-SVM多类分类器中进行故障识别，取得了满意的效果。

1 基于相关原则的优化阈值降噪方法

由于故障信息通常隐含在低频信号或一些比较平稳的信号中，而噪声一般是高频信号，采用小波变换可以根据信号特性将其分解到不同尺度 (对应不同的频段)下，对小波分解系数进行处理后直接重构即可达到去噪的目的［11］。

在强噪声干扰下，有用信号的小波变换系数往往比噪声的小波变换系数小，所以采用同一阈值来进行系数处理有可能把一些有用信号抹杀掉。而且因为传统去噪方法本身的缺陷，使得故障特征的提取有明显的偏差。为此，提出了一种阈值优化方法，即设计一个权列阵，它根据小波系数在各分解层相应位置的相关性，对阈值的权重进行优化，使各个层、各个点的去噪阈值更精确，从而提高去噪效果，更加完整的保留有用信号，增强信号的抗干扰能力。

1.1 基于相关原则的阈值优化降噪原理

信号与噪声在各尺度下的不同传播特性表明，信号的小波变换在各尺度间有较强的相关性，而且在边缘处更是具有很强的相关性;而噪声的小波变换在各尺度间却没有明显的相关性，信号主要是分布在低频部分或低尺度部分，而高频部分或高尺度部分噪声相对于信号来说则占主要。小波变换具有较强的去相关性，但变换后的小波系数之间仍然还存在着大量的相关性质。也就是说，小波系数在不同分辨率下的对应系数之间具有较强的相关性，低分辨率下的系数与高分辨率下的系数相关，即层间相关。根据信号与噪声的小波变换在各尺度间的上述不同特点，可以通过其相关性实现信号小波分解系数的定位来进行阈值的优化。定义小波相邻尺度同一空间位置系数的相关量为相邻尺度系数的乘积，记作:

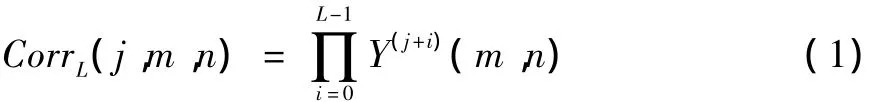
其中:L表示计算乘积的尺度数，(m，n)表示系数的空间位置 (作乘积之前先将各子带系数扩充成相同尺寸)，j表示尺度。由于边缘等特征的位置会随尺度的改变而发生一定偏移，传统的阈值去噪方法对每一层都采用同一阈值进行处理，易把信号与噪声同时去除。为解决传统阈值去噪所存在的问题，基于相关原则优化阈值法就是通过计算出相关系数，然后在相关系数大的位置，对阈值进行缩小，在相关系数小的位置对阈值进行放大，即对每层每个小波系数的阈值设置一个权重，对其进行调整优化。

1.2 基于相关原则的阈值优化方法去噪

为了对比该方法与传统小波去噪方法的优劣，使用不同的方法对故障信号进行仿真去噪处理，首先仿真模拟轴承外圈故障冲击信号如图1(a)所示，对其叠加低频干扰以及一定量的高斯白噪声得到含噪信号如图1(b)所示，然后分别使用传统的阈值去噪和基于相关原则的阈值优化方法去噪得到结果如图1 (c)、(d)所示。

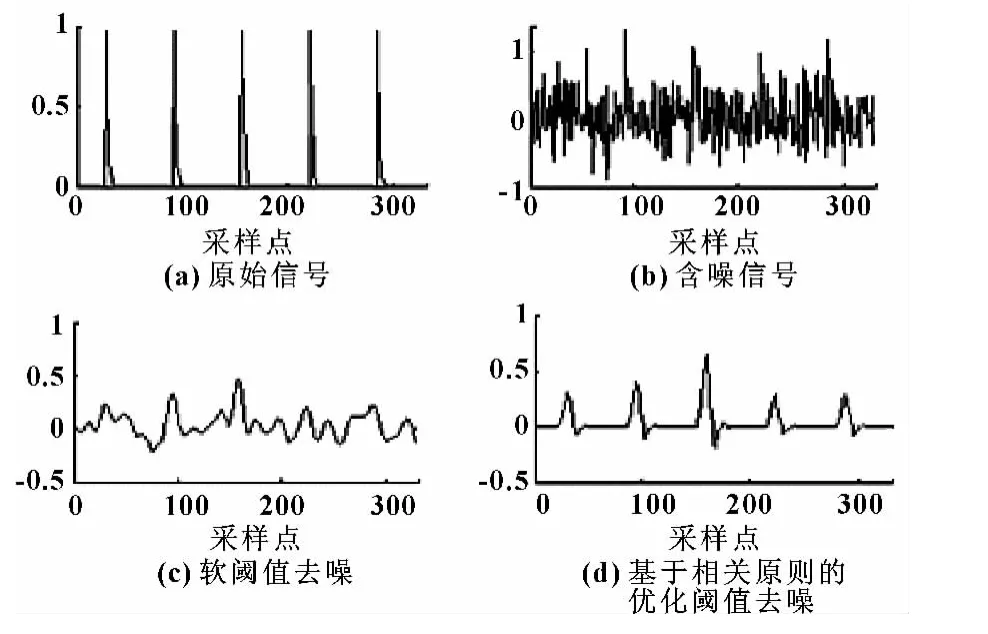
图1 基于相关原则优化阈值去噪效果对比

从图1(c)中可以看出:软阈值去噪后信号低频的干扰很多，信号周期性不明显，各峰值不能得到明确的体现，信号严重失真。妨碍了对故障特征的判断，采用了基于相关原则优化后的阈值，可以明显准确地提取信号特征值，低频干扰基本上被完全消除，克服了常规阈值去噪中的阈值计算不准确和每层采用单一阈值去噪的缺陷，并且实时性高，在仿真信号中能很好地体现这种算法在去噪后对故障特征的保留更为完整的优点，说明了该方法对传统阈值去噪效果有了明显的提高。

2 最小二乘支持向量机

2.1 支持向量机

SVM是基于结构风险最小化学习原则实现的，因此能提供很好的泛化性能。用二维输入空间的最优超平面集合结构来解释SVM，对于样本集 (xi，yi)，其中i=1，…，n。x∈Rd，y∈ {+1，－1}是类别标号。d维空间中线形判别函数的一般形式为:

而要求分类线对所有样本正确分类，就要求它满足:

因此，满足上述条件且使‖w‖最小的分类面就是最优分类面。如图2中用圆圈标出的点所示。

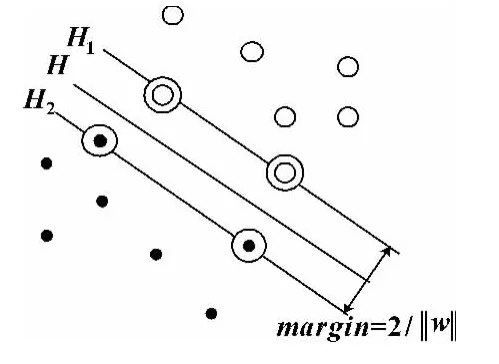
图2 最优分类面示意图

求解上述问题后得到的最优分类函数为

式中:sgn()为符号函数;αi＞0为Lagrange系数;b*为分类的域值。

2.2 最小二乘支持向量机

最小二乘支持向量机与标准的支持向量机的不同在于它把不等式约束改成了等式约束，并把经验风险的一次方改为二次方。最小二乘支持向量机的实现如下:

根据结构风险最小化原理，支持向量机问题可以表示为约束优化问题:

其中:d表示类标签。

为了求解上述优化问题，把约束优化问题转化成无约束优化问题，建立Lagrange函数:

从方程组 (7)中消去e，w后，可以得到支持向量机的输出为:

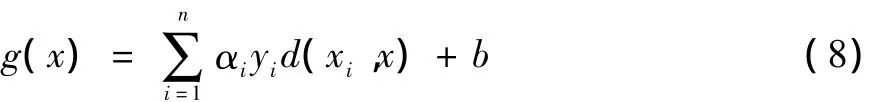
综上，最小二乘支持向量机的训练问题可归结为一个线性方程组的求解问题，这种转化使求解更为简单。而且最小二乘支持向量机将不等式约束条件转变成了等式的约束条件，使最小二乘支持向量机算法对支持向量失去了稀疏性，更加利于分类［12－13］。

3 滚动轴承故障的实验分析

3.1 实验台数据

文中采用的滚动轴承故障数据来源于美国凯斯西储大学轴承实验室，其实验平台如图3所示。

实验平台由4部分组成:1.5 kW电机，安装于驱动端的加速度传感器，功率计和控制电路。根据轴承实验室提供的数据，滚动轴承的型号为6205-2RS JEM SKF，直径为0.533 4 mm，转速为1 772 r/min，轴承的内径25 mm，外径52 mm，滚动体直径7.94 mm，节圆直径39 mm，滚珠个数为9个［14］。该实验采样频率选定为12 kHz，采样点数为12 000个，由滚动轴承故障频率计算公式［1］计算，轴承内圈、外圈和滚动体故障的理论特征频率分别为 159.48、106.32和139.20 Hz。

图3 滚动轴承故障信号采集平台

3.2 能量特征向量的提取

对以上的实验室数据作频谱分析得到其频谱图如图4所示。

图4 三种典型故障信号时域波形

对上述3种原始轴承故障信号分别进行四层基于相关原则优化阈值的小波变换分解，见图5。对于四层小波变换分解后，从图中可以清晰地看出内圈、外圈和滚动体的故障特征频率及其倍频成分。内圈故障的峰值点分别为160，320以及480 Hz，3个外圈故障最突出的峰值点为106和212，318 Hz也恰好是倍频关系，对比基于相关原则优化阈值的小波变换分解的结果，对于滚动体故障则在139 Hz，283 Hz相对突出，由此可以看出与理论值比较吻合。

同时，为比较基于相关原则优化阈值的小波变换与传统小波的分析效果，选用db2小波对故障信号进行5层小波分解，提取结果如图6所示。

图5 基于相关原则优化阀值的小波变换故障信号分解频谱图 (局部放大图)

图6 故障信号db2小波分析结果(局部放大图)

从图中可以看出，对于内圈、外圈和滚动体故障频率峰值与理论值均有一定偏差，倍频则完全无法判明。可见，文中采用的基于相关原则优化阈值的小波变换的降噪方法精度明显优于传统小波的降噪方法，且能够准确地提取出特征频率及倍频。

3.3 能量特征向量归一化

由于基于相关原则优化阈值的小波变换去噪后提供了不同频段的时频信息，因此可以提取各频段的能量作为特征向量。信号发生突变使得在突变位置的信号能量增大。因此，选取这些突变较大时刻的频带能量作为故障信号的特征向量。由上述基于相关原则优化阈值的小波变换分析结果，计算第四层8个分结点的系数绝对值:其中:j=4，代表基于相关原则优化阈值的小波变换尺度因子，k代表采样点数，文中每种故障类型选择6组数据，将其中4组作为训练样本，2组作为测试样本。然后利用该特征参数进行分类，各个节点的能量组成特征向量:

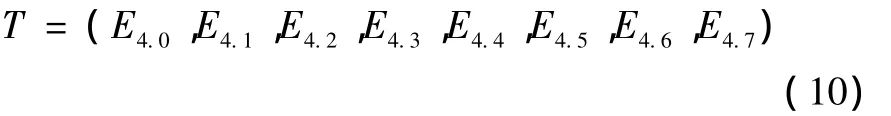
对E4.0～E4.7这8个节点的能量构造出需要的特征向量:

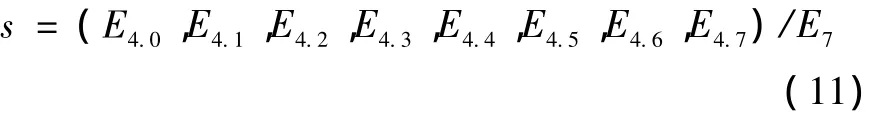
3.4 LS-SVM分类器分类

采用最小二乘支持向量机训练样本，核函数选择径向基函数。LS-SVM诊断模型采用“多对多”方法实现多类分类［9］，文中涉及到的故障类型有3种，需建立3个支持向量SVM1，SVM2，SVM3，以yi= {1，2，3}，分别表示内圈、外圈和滚动体故障，由式 (11)得到的归一化后的特征参数如表1所示。

表1 归一化后的能量特征向量

续表1

构造18个样本 {xi，yi}，i={1，2，…，18}。由于选择训练的样本数为12，核函数选择为delta= 0.5，gama=10的径向基函数，经训练后的分类结果如上表所示，从表格对比可知分类结果与故障类型完全吻合。

根据训练的模型进行样本的测试，得到的测试结果如表2所示。

表2 一对多分类测试结果

表中，1、2、3分别表示内圈、外圈、滚动体三类故障。支持向量机的输出值分别为1或者－1，其代表的含义为:输出为1，则属于该类，－1则不属于该类。通过表中输出的数据可知，测试的样本与最终判定的样本是完全吻合的，可以认为得到了最优分类面，最终判定经过最小二乘支持向量机训练后，该分类方法能对滚动轴承的故障类型进行精确识别。

通过实验仿真，可以认为LS-SVM能有效地进行滚动轴承的故障识别，由于在仿真分析和滚动轴承的实际应用中，所用到的样本数量都是较少的，因此可以认为结合基于相关原则优化阈值的小波变换及LSSVM应用于滚动轴承的故障诊断完全可行。

4 结论

(1)对比传统db2小波，利用基于相关原则优化阈值的小波变换变换方法提取滚动轴承振动信号的频域能量，作为诊断模型的特征向量能够准确地反映出故障的典型特征，将此特征向量输入到故障诊断模型中能够有效地提高诊断的正确率;

(2)LS-SVM对传统的SVM进行了改进，采用二次损失函数，将SVM中的二次规划问题转化为线性方程组求解，故障信号能正确分类，而测试样本输入支持向量机测试分析，验证了LS-SVM在大大降低了计算复杂性的同时保证了精度;

(3)基于相关原则优化阈值的小波变换与最小二乘支持向量机相结合用于滚动轴承故障诊断非常有效。该方法可以满足滚动轴承故障诊断的要求。

［1］梅宏斌.滚动轴承振动监测与诊断［M］.北京:机械工业出版社，1995:8－9.

［2］DONOHO D L.Denoising by Soft-threshold［J］.IEEE Trans on Information Theory，1995，41(3):613－627.

［3］DONOHO D L，LAIN M J.Ideal Spatial Adaptation by Wavelet Shrinkage［J］.Blometrika，1994，81(3):425－455.

［4］DONOHO D L，JOHN STONE I M.Adapting to Unknown Smoothness Via Wavelet Shrinkage［J］.Journal of American Statistical Association，1995，90(432):1200－1224.

［5］彭玉华.小波变换与工程应用［M］.北京:科学出版社，1999:1－62.

［6］赵瑞珍，宋国乡.一种基于小波变换的白噪声消噪方法的改进［J］.西安电子科技大学学报，2000，27(5):619－622.

［7］何焰兰，苏勇，高永楣.一种自适应小波去噪算法［J］.电子学报，2000，28(10):138－140.

［8］张维强，徐晨.一种基于平移不变的小波阈值去噪算法［J］.现代电子技术，2003，149(6):29－31.

［9］BURGES C.A Tutorial on Support Vector Machines for Pattern Recognition［J］.Data Mining and Knowledge Discovery，1998，2(2):1－43.

［10］SUYKENS J A K，VANDEWALLE J.Least Squares Support Vector Machine Classifiers［J］.Neural ProcessingLetters，1999，9(3):293－300.

［11］王秉仁，杨艳霞，蔡伟，等.小波阈值降噪技术在振动信号处理中的应用［J］.噪声与振动控制，2008，12:9－12.

［12］HSU C W，LIN C J.A Comparison of Methods for Multiclass Support Vector Machines［J］.IEEE Trans on Neural Networks，2002，13(2):415－425.

［13］李凌均，张周锁，何正嘉.支持向量机在机械故障诊断中的应用研究［J］.计算机工程与应用，2002(19):19－21.

［14］Case Western Reserve University Bearing Data Center［EB/ OL］.［2010－01－18］.http:www.eecs.cwru.edu/laboratory/bearing/welcomeovervie-w.htm.

Research on Roller Bearing Fault Diagnosis Based On Wavelet Noise Elimination and LS-SVM Algorithm

HAN Xing，XIONG Jingqi，WANG Lili，QIN Xiaopin
(School of Mechatronics Engineering，University of Electronic Science and Technology，Chengdu Sichuan 611731，China)

Aimed at the fault of roller bearing，the method of fault diagnosis of roller bearings based on correlative principles of optimum threshold plus wavelet noise elimination and Least Squares Support Vector Machine(LS-SVM)in combination was presented.Correlative principles of optimum threshold plus wavelet transformation was applied to extract the feature of fault of roller bearings at early stage，energy feature method was used for signal extraction.And then，the recognition of fault types were carried out by using LSSVM classified algorithm.Testing and simulation results show that the fault diagnosis method based on correlative principles of optimum threshold plus wavelet transformation and LS-SVM in combination can diagnose typical faults of the roller bearing effectively.

Roller bearing;Correlative principles of optimum threshold;Wavelet transformation;LS-SVM;Fault diagnosis

TH133

A

1001－3881(2014)9－154－5

10.3969/j.issn.1001－3881.2014.09.043

2013－04－06

国家自然科学基金资助项目 (61106107)

韩星 (1988—)，男，硕士研究生，研究方向为智能机电系统与故障诊断。E－mail:06hx825@163.com。