多途条件下近场声源三维被动定位

梁国龙，韩博，孙向前

(1.哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨150001;2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨150001;3.91388 部队，广东 湛江524022)

0 引言

常规波束形成是基于平面波假设的，信号到达各阵元之间的时延差仅是方位角的函数，适用于远场目标。而对近场目标而言，其波阵面以球面波扩展，时延差是距离和方位角的二维函数，因此常规波束形成不能应用于近场，需要采用聚焦波束形成技术［1］。聚焦波束形成可用于水平阵声图测量技术以完成近场被动目标的高精度定位［2-4］，但均是假定目标深度信息是已知的，在确知的深度平面上进行扫描完成二维定位。梅继丹等［5］给出了扫描深度误差的修正方法，但仅在扫描深度大于实际深度时误差可以被修正，并且要求目标过阵，应用条件比较苛刻。在海洋环境中，复杂的多途信道影响了聚焦波束形成的应用。时洁等［6］采用虚拟时间反转镜技术用以克服多途信道的影响，文献［7］中利用垂直矢量阵的物理优势达到良好的抗多途效果。然而，多途信号虽然会制约聚焦波束形成的应用，但它同样可以被利用以获得深度信息。吴艳群等［8］采用单矢量水听器在多途环境下完成信源三维定位，利用水平声压阵同样多途的条件下估计目标的三维坐标［9-10］。但是以上方法均需要利用相关求时延。

本文在水平线列阵的条件下，利用近场被动声图测量技术，在扫描深度不确定的情况下，得到直达声信号和多途信号的聚焦峰，通过确定直达声和海面一次多途两个峰值的位置及扫描深度即可解算出目标的三维坐标，在扫描深度大于或小于目标实际深度时都可以实现误差修正。为了验证该方法的有效性，进行了计算机仿真。

1 常规水平阵被动声图测量技术

被动声图测量应用的是聚焦波束形成扫描技术。如图1所示，首先确定声图扫描平面，然后在这个有限平面上确定扫描范围，扫描点数越多声图的分辨率越高，但随之计算量也增大。在每个扫描点处，对各个阵元接收的数据做球面波时延补偿后相加，扫描完整个测量区域后可以得到一幅声图。当扫描到点声源位置时，各个阵元信号同相叠加得到最大值，即在声图上显示一个亮点。在多途信号存在的情况下，声图上会显示比声源位置强度弱的另一些亮点，并使得声图整体旁瓣级升高。

图1 多途条件下声图测量模型Fig.1 Model of focused beamforming in multipath environment

考虑图1的情况，水平阵固定于运动平台上，阵列与x 轴平行，中心阵元坐标为(0 m，0 m，25 m)，即阵列深度为h=25 m，海深H=60 m，阵元数N=31，阵长L =37 m，声源预设坐标(x0，y0，z0)为(10 m，30 m，15 m)，处理的信号带宽范围是1 000 ～2 000 Hz，SNR=10 dB，声速取1 480 m/s，噪声为互不相关的空间高斯白噪声。扫描深度z' =15 m，范围为70 m×70 m 的平面，步长1 m.由于在近程范围内，多次反射产生的多途信号相对于直达声和一次反射多途信号要弱得多，而且它们的亮点较直达声和一次多途信号的亮点距离较远，这点从后面的分析可以看出。所以仿真中仅考虑海面一次多途信号和海底一次多途信号，海面及海底的反射系数分别为为-0.9 和0.5.图2给出了多途条件下的声图测量结果。从图2可以看出，通过声图测量可以找到目标位置，但由于多途的存在，出现了3 个聚焦点。其中，直达声和海面一次多途聚焦点比较明显，海底多途信号由于传播距离相对较远，且海底声吸收较海面强，它的聚焦点(坐标为(30 m，88 m))并不明显。多途引发的多个聚焦点的存在，会引起多目标的假象，但是，多途的存在，也可以用于修订目标的定位结果，甚至可以进一步获得目标的深度信息。

2 三维被动定位算法

2.1 扫描深度误差对声图测量影响

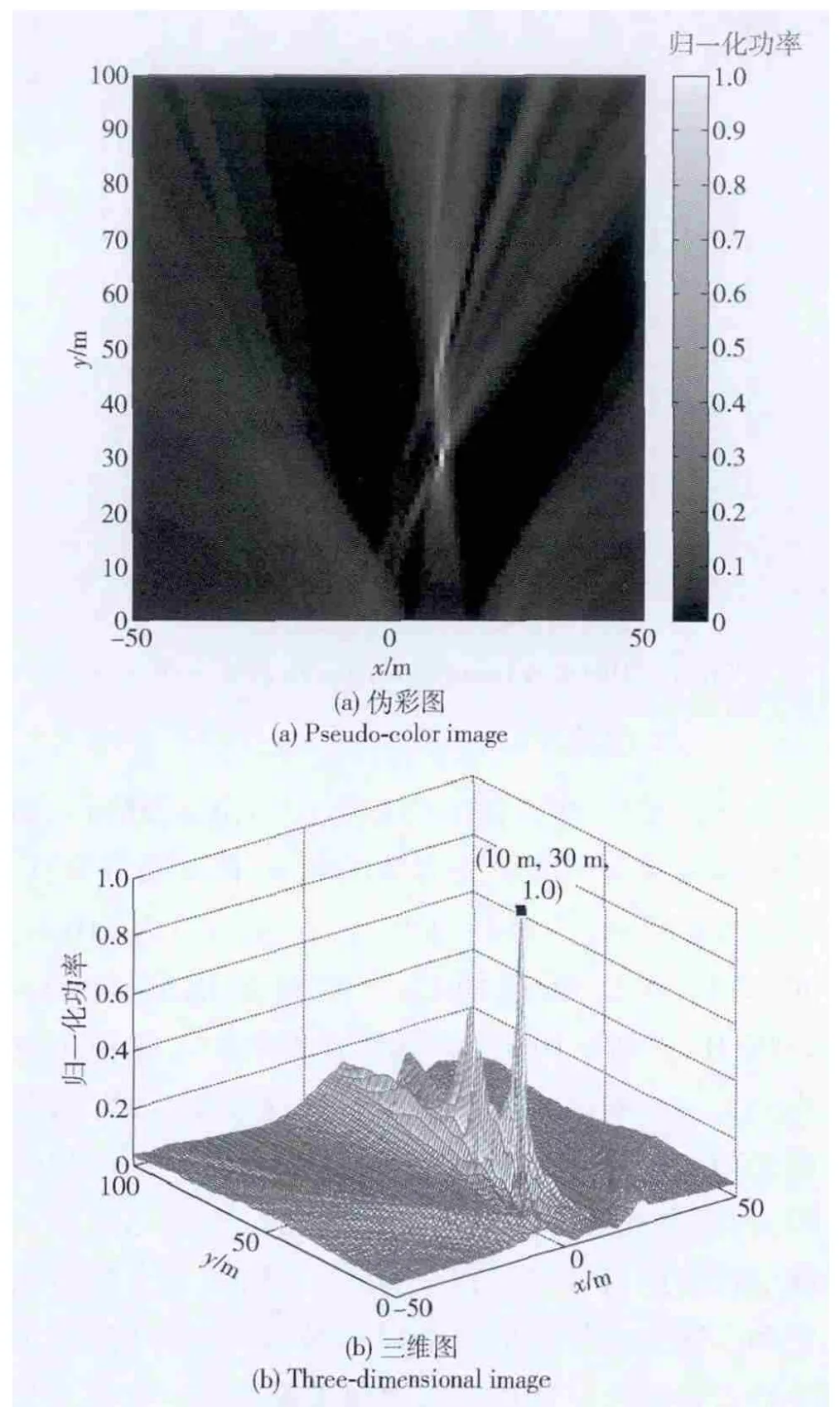
图2 多途条件下聚焦波束形成结果Fig.2 Result of focused beamforming in multipath environment

对于水平声压阵来说，由于每一个水听器都是无指向性的，所以在每一个垂直于阵的平面上，它的自然指向性都是一个圆环，如图3所示。在这个圆环上的任意一点到各个阵元的时延都是一致的，水平声压阵无法区分目标在圆环的哪个位置。因此，当扫描深度和目标深度不符时，就会出现y 轴和z 轴方向的定位误差。由于等时延圆是垂直于水平阵的，所以扫描深度误差不影响对x 轴坐标的定位。

2.2 扫描深度小于目标实际深度

扫描深度小于目标实际深度的情况如图4所示，等时延圆所在平面为垂直于x 轴的截面。目标S0的坐标真值为(x0，y0，z0)，在扫描深度上的通过声图测量得到的等效点S'的坐标为(x'，y'，z')，虚源S1的等效点S″的坐标为(x″，y″，z″)。由于水平声压阵有左右舷模糊的现象，在本文中，均假设目标左右方向已知，方向为y 轴正向。因此，由声图测量结果即可获得S'和S″的坐标。

图3 水平声压阵等效点示意图Fig.3 Schematic diagram of horizontal array equivalent points

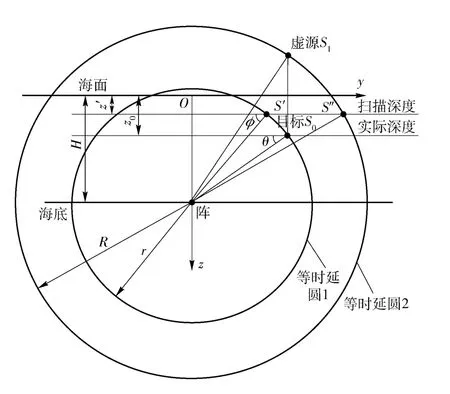
图4 海面多途条件下等时延点几何关系示意图(z' ＜z0)Fig.4 Geometric relationship (z' ＜z0)

令等时延圆1 和等时延圆2 的半径分别为r 和R，利用余弦定理可得

由直角三角形的关系易知，sinθ =(h - z0)/r，cos φ=y'/r，联合(1)式和(2)式并化简可得

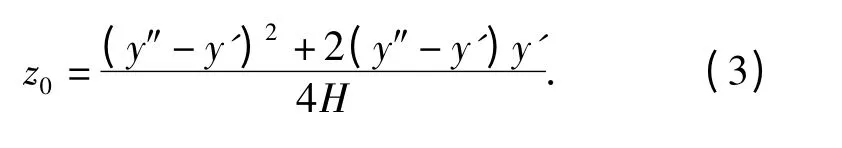
通过解三角关系可得

将(3)式代入(4)式即可得到y0，由2.1 节的分析，扫描深度误差不影响目标x 轴的定位，所以可得

由(3)式～(5)式即可得到目标S0的三维坐标。

2.3 扫描深度大于目标实际深度

图5即为扫描深度大于目标实际深度的几何关系示意图。在这种情况下，只是z0与z'以及y0与y'的大小关系改变了，(1)式～(5)式依然成立，目标的坐标值为

由此可见，不论扫描深度大于或小于目标的实际深度，该算法都可以通过声图测量将实际目标点的三维坐标给出。

图5 海面多途条件下等时延点几何关系示意图(z' ＞z0)Fig.5 Geometric relationship (z' ＞z0)

2.4 海底一次反射多途信号对算法的影响

从本文第一部分的仿真可以看出，声图上海底一次反射多途信号的聚焦点并不明显，并且在y 轴上的位置比海面多途信号聚焦点远，这是因为仿真条件的阵列深度和海深相差较大。实际中，阵列深度可以控制，只要选择好阵深和海深的关系，就可以比较容易地分清楚哪个是海面多途聚焦点。如图6所示，如果海面虚源S1到阵平面的距离小于海底虚源S2到阵平面的距离，那么S2的聚焦点S‴在y 轴上的位置就比S1的聚焦点S″远。即保证2z0+(h-z0)＜(H-z0)+(H-h)，化简为

若目标始终在阵列上方运动，那么海底多途聚焦点比海面多途聚焦点y 轴位置远的条件是

如果不满足上述条件，两个多途信号聚焦点的位置关系不固定，声图上能量输出大小关系又不明显，那么从声图上就很难区分这两个聚焦点对应于哪个多途信号。在这种情况下，由于直达声信号是很好辨认的，所以将直达声聚焦点波束方向的数据与其他两个聚焦点波束方向数据做相关，如果相关峰是负的，这个聚焦点就是海面多途形成的，如果相关峰是正的，那么就是海底多途形成的聚焦点。

图6 海面海底多途条件下等时延点几何关系示意图Fig.6 Geometric relationship in multipath environment

2.5 虚源S1等时延点y 轴坐标的确定

从(3)式可以看出，目标深度z0估计准确性与声图上的y 轴坐标y'和y″有关。y'为目标的等时延圆与扫描平面的交点，是整个声图上输出能量最大点，容易确认。而y″是海面一次多途反射信号在声图上形成的峰值，输出能量小于目标直达声信号，正如图4所示。那么，从(3)式中解出y″可得

假设目标的最小深度为zmin，那么，可以得到y″的范围是

所以在(8)式的范围内搜索峰值来确定y″，可以降低虚源聚焦峰值搜索错误的不利影响。综上所述，本文的三维被动定位算法主要步骤如下:

1)在满足(8)式的条件下，取阵列以上任意扫描深度上对声图测量区域做二维扫描，得到目标信号聚焦点坐标;

2)在(10)式给出的扫描范围内确定聚焦峰位置，如果在此范围内存在两个峰值，则取y 轴坐标小的峰值作为虚源S1的聚焦峰;

3)根据声源和虚源S1在声图上聚焦点的几何关系，并结合扫描深度、阵列深度，利用(6)式计算出目标三维坐标的估计值。

3 计算机仿真及分析

通过计算机仿真验证本文提出的三维被动定位算法，并检验其性能。在仿真实验中，使用本文第一部分的仿真参数，仅将扫描深度设定为z' =20 m.从图7(b)可以看出，由于扫描深度和目标深度不符合，使得y 轴方向的定位产生偏差。利用本文算法对目标三维坐标修正，可得目标的估计坐标(^x0，^y0，^z0)为(10 m，29.9 m，15.4 m).从结果看，由于扫描深度和目标深度不符所带来的定位误差是可以修正的，与理论分析一致。

图7 多途条件下聚焦波束形成结果Fig.7 Result of focused beamforming in multipath environment

依然使用上述的仿真参数，改变扫描深度，计算定位的均方误差。图8给出了目标定位的均方误差随扫描深度变化的结果，每个点都是100 次Monte Carlo 实验平均的结果。从图8可以看出，随着扫描深度的变化，目标的深度的均方误差在0.5 m 以下，y 轴方向的定位误差在0.7 m 以下，x 轴方向的定位误差为0.扫描深度的不同不会使得目标和多途信号聚焦点的x 轴坐标改变，仅会影响y 轴坐标的位置，而两个聚焦点的相对位置变化很小，几乎不影响两个聚焦点的分辨能力，这一点从图4或图5可以很清楚的看到。由此可知，扫描深度变化对定位精度的影响较小。

图8 目标位置随扫描深度变化的均方误差曲线Fig.8 RMSE versus scanning depth

图9～图11分别给出了扫描深度z' =20 m 的情况下，目标定位的均方误差随坐标变化的结果，每个点都是100 次Monte Carlo 实验平均的结果。

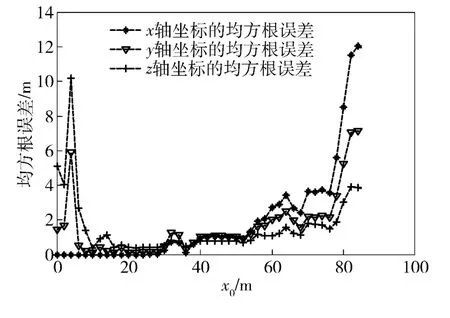
图9 目标位置随x0 变化的均方误差曲线Fig.9 RMSE versus x0

图9所示的是目标y 轴和z 轴坐标为初始值，目标坐标的均方误差随x 轴坐标的变化情况，只考虑x 轴正向的定位误差，由于水平直线阵在直角坐标下是完全对称的，x 轴负向同正向结果类似。由图9可知，随着x0的增加，对x0、y0和z0估计的均方误差都呈增大趋势，这是因为阵列孔径的限制使得远离阵列的位置近场聚焦能力下降，并且阵列测量的开角增大，使得测量精度降低。y0和z0估计值的均方误差变化趋势大致相同，而在靠近阵中心的区域里(x0＜6 m)，由于多途聚焦点与直达声聚焦点混叠，使得聚焦点位置确定比较困难，误差很大，导致y0和z0估计值与真值相差较多，在6 m ＜x0＜80 m的区域内，两个聚焦点易于分辨，定位效果好，均方误差都在2 m 以下。在x0＞80 m 的区域里，定位算法失效。

图10 目标位置随y0 变化的均方误差曲线Fig.10 RMSE versus y0

图10所示的是目标x 轴和z 轴坐标为初始值，目标坐标的均方误差随y 轴坐标的变化情况，同样只考虑y 轴正向的定位误差。从图10中可以看出，随着y0的增加，在y0＜55 m 的范围里，x0和y0估计值的均方误差基本稳定在1 m 以下，效果很好。而y0的增加使得z0估计的误差增大，主要原因是随着y0的增加，对多途聚焦点y 轴坐标的确定很困难，由(3)式可知，这导致z0的估计误差很大。但是在y0比较大的区域，发现z0的估计误差增大对y0的估计影响很小，从(4)式可知，这是因为在仿真条件下的深度范围内，大y0的情况下，z0的估计值对y0的影响很小，该方法退化为常规被动声图测量。

图11所示的是目标x 轴和y 轴坐标为初始值，目标坐标的均方误差随z 轴坐标的变化情况。深度大于阵列深度的部分(z0＞25 m)仅作理论分析用。从图11中可以看出，当z0值比较小的时候，对目标定位的精度稍差，因为当z0值比较小的时候，直达声的聚焦峰和多途的海面多途聚焦峰混叠不易区分。在z0＞5 m 的区域，y0和z0估计值的均方误差均小于2 m.而在z0＞28 m 的区域，对y0和z0的估计误差过大，算法失效。

图12给出了随着信噪比的变化，目标坐标估计的均方误差曲线。由图12可知，算法对信噪比的变化不敏感，在信噪比不是很小的情况下(SNR ＞-15 dB)，目标位置估计的均方误差在1 m 以下，效果较好。这是因为阵列处理的增益和对信号的处理带宽增益的影响使得目标定位精度在较低信噪比的条件下依然良好。

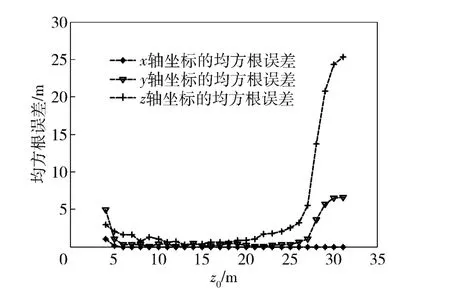
图11 目标位置随z0 变化的均方误差曲线Fig.11 RMSE versus z0

图12 目标位置随SNR 变化的均方误差曲线Fig.12 RMSE versus SNR

4 结论

本文提出一种多途条件下近场源三维被动定位方法，该方法利用了多途信道的特征，解决了水平阵三维被动定位这一问题。与其他利用多途信号的三维被动定位方法不同，本文方法无需进行相关运算获得时延信息，仅利用声图上直达声信号和海面一次反射信号的聚焦峰位置和扫描深度确定信源三维坐标。仿真结果与理论分析相符合，表明该方法具有一定工程参考价值。本文方法是对声图三维被动定位的初探。对于阵列的实际应用条件，运动平台存在的本地干扰会影响近场源的定位，如何抑制本地干扰是今后需要研究和讨论的方向。

References)

［1］ Kim K M，Yang I S，Chun S Y，et al.Passive-range estimation using dual focused beamformers［J］.IEEE Journal of Oceanic Engineering，2002，27(3):638 -641.

［2］ 惠娟，胡丹，惠俊英，等.聚焦波束形成声图测量原理研究［J］.声学学报，2007，32(4):356 -361.HUI Juan，HU Dan，HUI Jun-ying，et al.Researches of the measurement of distribution image of radiated noise using focused beamforming［J］.Acta Acustica，2007，32(4):356 -361.(in Chinese)

［3］ 梅继丹，惠俊英，惠娟.聚焦波束形成声图近场被动定位技术仿真研究［J］.系统仿真学报，2008，20(5):1328 -1333.MEI Ji-dan，HUI Jun-ying，HUI Juan.Research on simulati-on of near field passive ranging with underwater acoustic image by focused beam-forming［J］.Journal of System Simulation，2008，20(5):1328 -1333.(in Chinese)

［4］ 梅继丹，惠俊英，惠娟.水平阵聚焦波束形成声图定位算法研究［J］.哈尔滨工程大学学报，2007，28(7):773 -778.MEI Ji-dan，HUI Jun-ying，HUI Juan.Measurement of underwater acoustic image positions using a horizontal linear array with focused beam-forming［J］.Journal of Harbin Engineering University，2007，28(7):773 -778.(in Chinese)

［5］ 梅继丹，王逸林，翟春平，等.扫描深度误差对声图测量的影响及其修正方法研究［J］.声学学报，2010，35(4):414 -418.MEI Ji-dan，WANG Yi-lin，ZHAI Chun-ping，et al.Research on the influence and correction method of depth scanning error to the underwater acoustic image measurement［J］.Acta Acustica，2010，35(4):414 -418.(in Chinese)

［6］ 时洁，杨德森，刘伯胜.基于虚拟时间反转镜的噪声源近场定位方法研究［J］.兵工学报，2008，29(10):1215 -1219.SHI Jie，YANG De-sen，LIU Bo-sheng.Radiated noise sources near-field location based on virtual time reversal mirror［J］.Acta Armamentarii，2008，29(10):1215 -1219.(in Chinese)

［7］ 梅继丹，王珺琳，惠俊英.垂直矢量阵声图被动定位技术研究［J］.兵工学报，2010，31(3):369 -374.MEI Ji-dan，WANG Jun-lin，HUI Jun-ying.Research on the underwater acoustic image passive locating using vertical linear array［J］.Acta Armamentarii，2010，31(3):369 -374.(in Chinese)

［8］ 吴艳群，胡永明，倪明，等.基于单矢量水听器多途宽带信号的三维定位算法［J］.兵工学报，2010，31(9):1181 -1187.WU Yan-qun，HU Yong-ming，NI Ming，et al.Three-dimention localization of broadband sources using a single vector hydrophone in multipath environment［J］.Acta Armamentarii，2010，31(9):1181 -1187.(in Chinese)

［9］ Yuan Y X，Carter C，Salt J E.Near-optimal range and depth estimation using a vertical array in a correlated multipath environment［J］.IEEE Transaction on Singal Processing，2000，48(2):317 -330.

［10］ Lee S H，Ryu C S，Lee K K.Near-field source localization using bottom-mounted linear sensor array in multipath environment［J］.IEE Proceedings-Radar Sonar and Navigation，2002，149(4):202 -206.