单压差型矢量水听器方位估计的优化研究
2014-06-27王绪虎陈建峰韩晶张群飞
王绪虎,陈建峰,韩晶,张群飞
(1.西北工业大学航海学院,陕西西安 710072;2.曲阜师范大学物理工程学院,山东曲阜 273165)
单压差型矢量水听器方位估计的优化研究
王绪虎1,2,陈建峰1,韩晶1,张群飞1
(1.西北工业大学航海学院,陕西西安 710072;2.曲阜师范大学物理工程学院,山东曲阜 273165)
针对压差型矢量水听器的直径波长比大于0.2时,利用它进行方位估计性能恶化的问题,提出一种修正的单个压差型矢量水听器多重信号分类(MUSIC)算法。修正方法通过修正压差型矢量水听器的阵列流型,提高了单个压差型矢量水听器MUSIC算法方位估计的估计精度,且在直径波长比大于0.2时依然保持较好的估计精度和稳健性。仿真结果表明,单个矢量水听器MUSIC算法相对于声强法在低信噪比时具有更好的方位估计性能,修正的压差型矢量水听器MUSIC算法在直径波长比大于0.2时依然具有良好的估计性能。湖上试验的数据处理结果进一步验证了单个压差型矢量水听器的修正MUSIC方位估计方法在实际系统中是有效的,且其估计性能优于原MUSIC方法。
信息处理技术;压差型矢量水听器;方位估计;多重信号分类算法
0 引言
矢量水听器及相应的信号处理技术是当今水声领域重点发展的新技术之一。随着工艺和技术的发展,性能优良的矢量水听器现已进入工程应用阶段[1]。常用的矢量水听器有“同振型”和“压差型”两种[2]。同振型矢量水听器采用加速度计作为敏感元件,制作工艺要求苛刻,价格较贵,一般适合较低的工作频段。压差型矢量水听器又称声压梯度型矢量水听器,可使用较高的工作频段,价格低廉、结构简单、装配方便[3]。
单矢量水听器的方位估计处理方法有波束扫描法,平均声强法和复声强法等[4]。波束扫描法类似于声压阵的处理,通过搜索波束输出的最大值来确定目标方位[5];平均声强法利用了声强输出的矢量性,在各向同性带限高斯白噪声中被证明是最大似然比方位估计[6];复声强法实质是对声压和振速信号进行互谱处理,在频域利用声强的矢量性进行方位估计,当信号不在同一个频段工作时,该方法具有分辨多目标方位的能力[4]。近期,梁国龙等[7]、陈羽等[8]又提出了基于单矢量水听器的高分辨方位估计处理方法。
由于压差型矢量水听器对机械运动扰动不敏感,便于吊装安装的优点,它在浮标,潜标和超短基线水声定位等系统中使用较多[9]。本文在分析单压差型矢量水听器的方位估计方法的基础上,将多重信号分类(MUSIC)算法引入单压差型矢量水听器方位估计理论中。根据压差型矢量水听器的特点,提出一种修正的单压差矢量水听器MUSIC方法,该方法在阵元间距大于压差型矢量水听器的“工程近似条件(d≤0.2λ,d为水听器直径,λ为其波长)”时[10],依然保持了良好的估计性能。最后,通过计算机仿真和湖试数据的处理,对比了单压差型矢量水听器MUSIC算法和声强法的方位(DOA)估计性能,证实了单压差型矢量水听器修正MUSIC算法的有效性。
1 压差型矢量水听器工作原理
二维压差型矢量水听器是由4个声压水听器复合而成,相当于1个四元离散声压圆阵。为了获得精确的声压梯度,要求四元阵的半径较小(相对于信号波长来说),且阵元一致性高。
图1给出了二维压差型矢量水听器的结构。在远场平面波的环境中,4个阵元的输出可以表示为
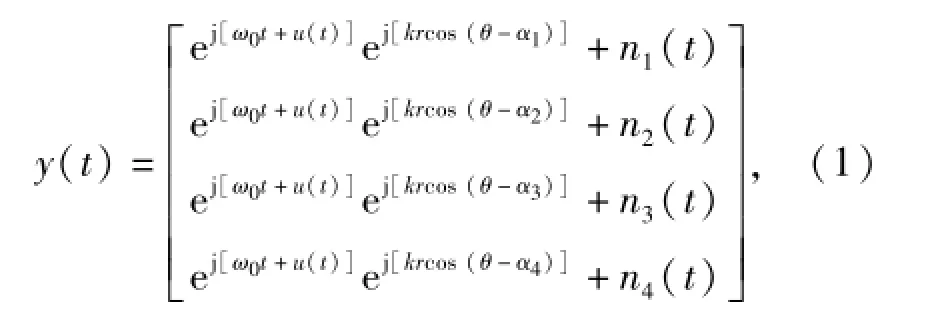
式中:ω0表示信号的中心角频率;u(t)为信号的初相位;k表示信号波数的大小;r表示四元阵的半径;αi(i=1,…,4)表示相应阵元与坐标原点的连线与x轴的正半轴的夹角;ni(i=1,2,3,4)为对应阵元的噪声。忽略掉噪声项,压差矢量水听器的声压可表示为

中心点处的振速分量(实质为声压差,这里只对压差进行移相90°,没有除以阵元间距,相当于对其进行了幅度预处理)可表示为

式中:e-jπ/2项是为了保持声压与振速的相位一致性而引入的。当kr≪1时,上述两式可近似为
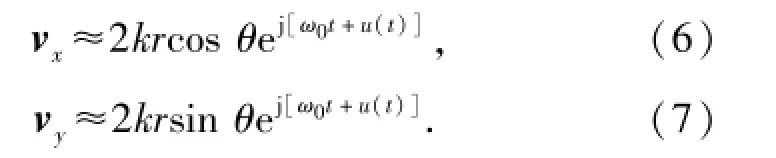

图1 压差型矢量水听器的结构图Fig.1 Structure layout of pressure differential vector hydrophone
忽略掉幅度的影响(实际系统中可以进行预补偿),二维压差矢量水听器的输出可以写为
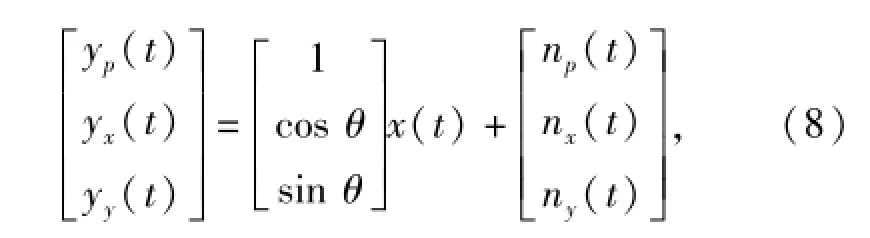
式中:x(t)=ej[ω0t+u(t)]表示中心点处声压信号。
在工程上,一般认为对角阵元间距满足d≤0.2λ时,便符合了kr≪1的条件[10]。因此,将d≤0.2λ称为压差型矢量水听器的“工程近似条件”,满足这个条件时压差型矢量水听器性能稳定,其振速输出具有偶极子的指向性。不满足这个条件,则压差型矢量水听器的性能下降。
2 压差型矢量水听器DOA估计原理
2.1 声强估计法
由(8)式可以得出
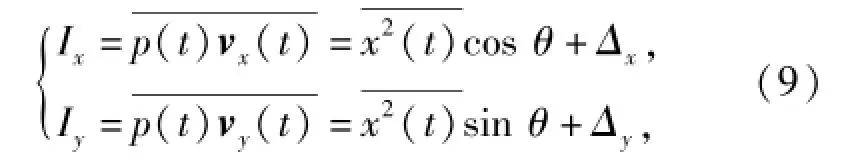
式中:Ix和Iy分别表示x轴和y轴上的平均声强;Δx和Δy表示噪声贡献在x轴和y轴上的平均声强部分。在信噪比比较高时(忽略掉噪声项),两式相除可得

利用(10)式进行DOA估计的方法称为平均声强法。当存在多目标时,该方法则失效,此时可以利用目标频谱上的差异来进行分辨。
对各个通道的接收信号进行傅里叶变换,得到相应的谱P(ω)、Vx(ω)和Vy(ω),则声压和振速的互谱可表示为
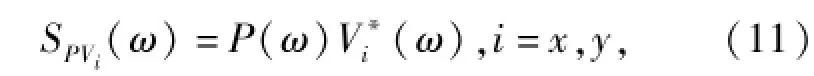
式中:符号表示共轭运算。结合傅里叶变换的基本特性,可得
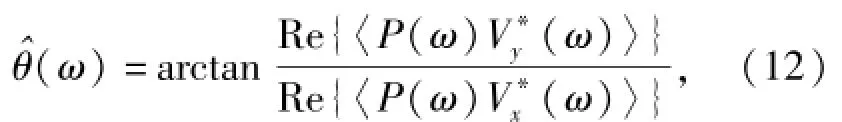
式中:〈·〉表示滑动平均周期图。(12)式表示的信号DOA估计方法称之为复声强器法,其检测、测向和多目标方位分辨性能均优于平均声强器法[4]。
2.2 声强估计法的优化
对于压差型矢量水听器来讲,(10)式、(12)式成立的前提条件是满足kr1.实际应用中,若不能满足这个条件的,会造成DOA估计性能的下降,因此需要寻找一种有效的方法来改善这种情况[9]。


为了将上述方法区别于声强法,将利用上述原理求解目标方位的方法称为修正声强法。
3 单压差水听器高分辨DOA估计原理
3.1 MUSIC算法的基本原理
阵列接收窄带远场信号的数学模型为

式中:X为阵列接收信号向量;A为阵列流型矩阵;s为信号向量;θ表示目标的方位向量;N为各通道的噪声向量。由于信号与噪声是相互独立的,因此阵列的协方差矩阵可以分解为两部分

式中:RS为信号的协方差矩阵;σ2为阵元的噪声功率,假定各个阵元上的噪声功率是相同的;I为单位矩阵。对R进行特征分解,可以得到
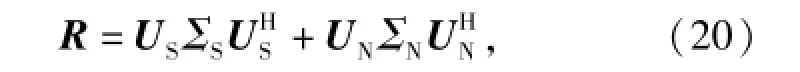
式中:US为信号子空间;UN为噪声子空间,理想条件下,二者是正交的[11-12]。即

由于噪声的存在,且实际接收信号为有限长的, a(θ)与UN不可能完全正交。因此可以通过最小化搜索来求解目标方位,即
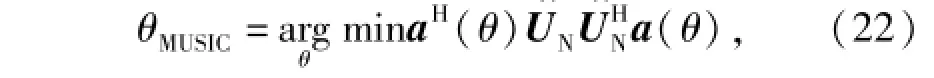
所以,MUSIC算法的谱估计公式为
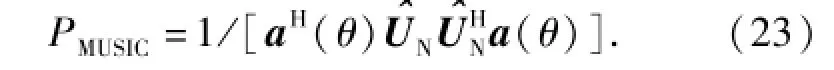
MUSIC算法需要先估计信号源的个数,再估计目标方位。信源个数的估计不是要研究的内容,本文中,假定确知目标的个数。
3.2 单压差矢量水听器MUSIC算法
(8)式可写为
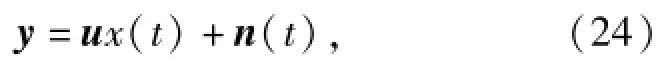
式中:y=[yp,yx,yy]T为矢量水听器接收信号向量;u=[1,cos θ,sin θ]T为单位矢量;n表示噪声向量。对比(18)式和(24)式,可发现二者具有相似的形式,因此可将单位矢量看作矢量水听器上的阵列流型,即矢量水听器阵列流型的特点在文献[7]中进行了论述,这里不做具体分析。
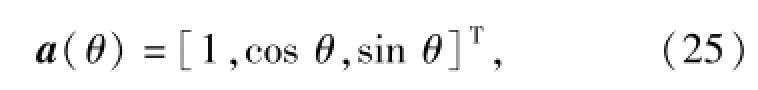

实际系统中,矢量水听器的协方差矩阵的最大似然估计为式中:N表示矢量水听器数据的快拍数。对y进行特征分解可以求得矢量水听器的噪声子空间n.类比(23)式可以得到矢量水听器MUSIC算法的谱估计公式为
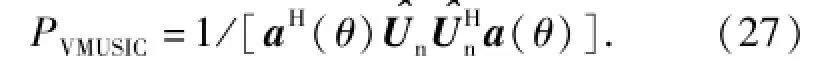
显然,(27)式也是利用了信号子空间与噪声子空间的正交性来估计目标方位的。与传统的MUSIC算法一样,求解过程中需要进行谱峰搜索,搜索步长影响目标DOA估计的精度。
3.3 单压差矢量水听器MUSIC算法的优化
对于压差矢量水听器来讲,当不满足kr≪1的条件时,利用(27)式表示的空间谱来解算目标方位性能会下降。
由前面的分析可知,当不满足kr≪1时,压差矢量水听器输出可以写为
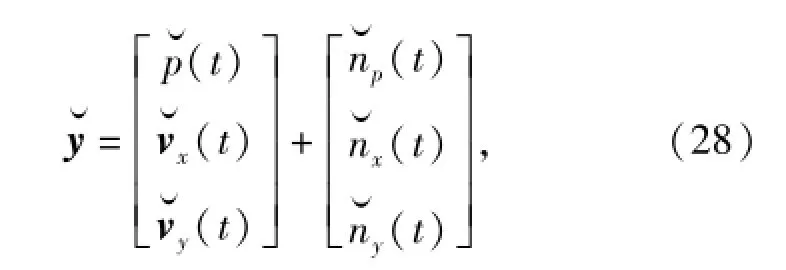

将(2)式、(4)式和(5)式代入(28)式可得结合(24)式和(25)式的分析可得,不满足kr≪1时压差矢量水听器的阵列流型可表示为
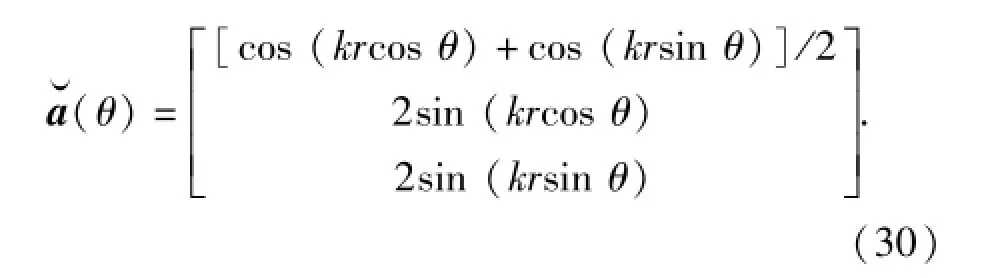
因而单压差矢量水听器MUSIC算法的空间谱可表示为
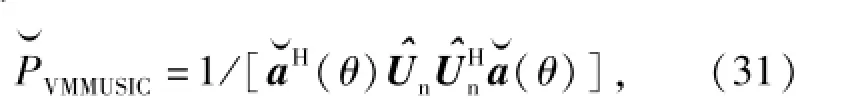
为了区别,(31)式表示的方法称之为单压差矢量水听器的修正MUSIC算法。
4 仿真实验与分析
仿真过程中,环境噪声采用带宽2 kHz的空间各向同性的数值模拟高斯白噪声[13],信号是中心频率为7 kHz的窄带信号,样本时间为50 ms,采样频率为50 kHz.计算结果为100次独立实验的统计数据。
图2给出了不同直径情况下压差矢量水听器声强法DOA估计的性能曲线。从图2中可以看出,复声强法和修正声强法的DOA估计误差随半径的增大逐渐增大,但修正声强法的性能远优于复声强法。对比上下两图可以看出,信噪比高时修正声强法的性能好,信噪比低时其性能变差。复声强法在不满足“工程近似条件d≤0.2λ”时,其性能的变化基本不受信噪比的影响。这说明此时,“近似误差”起主要作用。
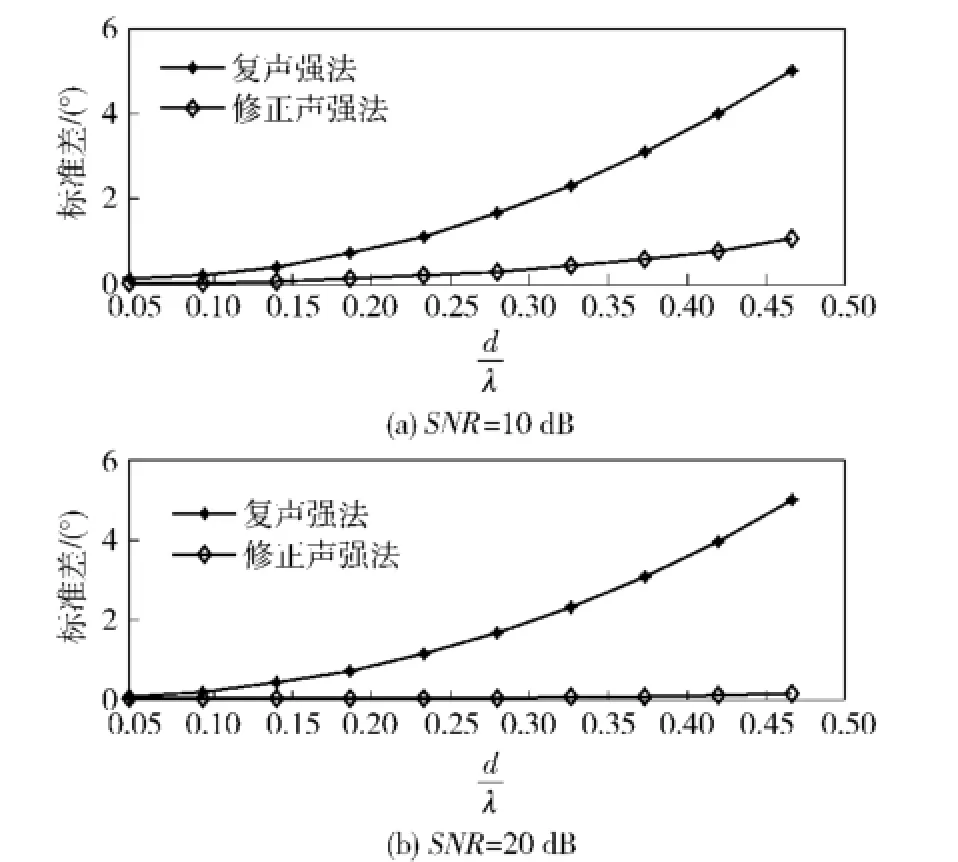
图2 不同直径下声强法DOA估计性能Fig.2 The performances of DOA estimation of sound intensity methodsfor hydrophones with different diameters
图3为不同信噪比情况下声强法方位估计的性能曲线。图3(a)为直径d=0.04 m时,两种估计方法的性能曲线,此时直径波长比为0.187;图3(b)为直径d=0.08 m时,两种方位估计方法的性能曲线,此时直径波长比为0.373.从图3看出,在相同直径情况下,修正声强法的标准差小于复声强法的标准差,且修正声强法的标准差随着信噪比的增加逐渐减小。复声强法的标准差随信噪比的增加性变化不大,且压差矢量水听器对角间距越大其方位估计的标准差越大。上述这一现象说明了在不满足工程近似条件时,“近似误差”的影响对压差型矢量水听器的估计性能起主要作用。这一点说明了在应用中,声强法对压差矢量水听器阵元间距的要求比较苛刻,而修正声强法则降低了对阵元间距的要求,体现出更强的稳健性。

图3 不同信噪比下声强法DOA估计性能Fig.3 The performances of DOA estimation of soundintensity methods for different SNRs
图4为不同直径情况下单压差矢量水听器MUSIC算法和修正MUSIC算法的性能曲线。从图4中可以看出,单矢量水听器MUSIC算法在阵元直径增大时性能逐渐下降,修正MUSIC算法性能随阵元直径增大变化较慢,且其性能在相同条件下优于MUSIC算法。这充分体现了修正MUSIC算法对阵元间距的变化有更强的鲁棒性。
图5为不同信噪比情况下压差矢量水听器MUSIC算法和修正MUSIC算法的性能曲线。从图5中可以看出,随着信噪比的增高,两种方法的估计性能逐渐变好;在相同信噪比条件下,修正MUSIC方法的估计标准差小于MUSIC算法DOA估计的标准差。通过上下图的比较,可以看出,对角阵元间距的变化对压差型矢量水听器MUSIC算法影响很大,对压差型矢量水听器的修正MUSIC算法影响较小。这说明阵元间距大时“近似误差”影响了MUSIC算法的性能,而修正MUSIC算法对阵元间距的变化显示出了更好的稳健性。
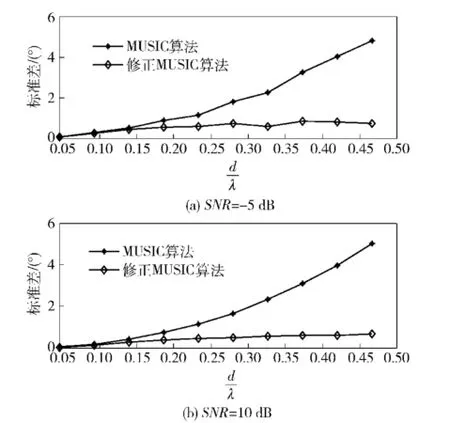
图4 不同直径情况下MUSIC算法的DOA估计性能Fig.4 The performances of DOA estimation of MUSIC algorithms for hydrophones with different diameters
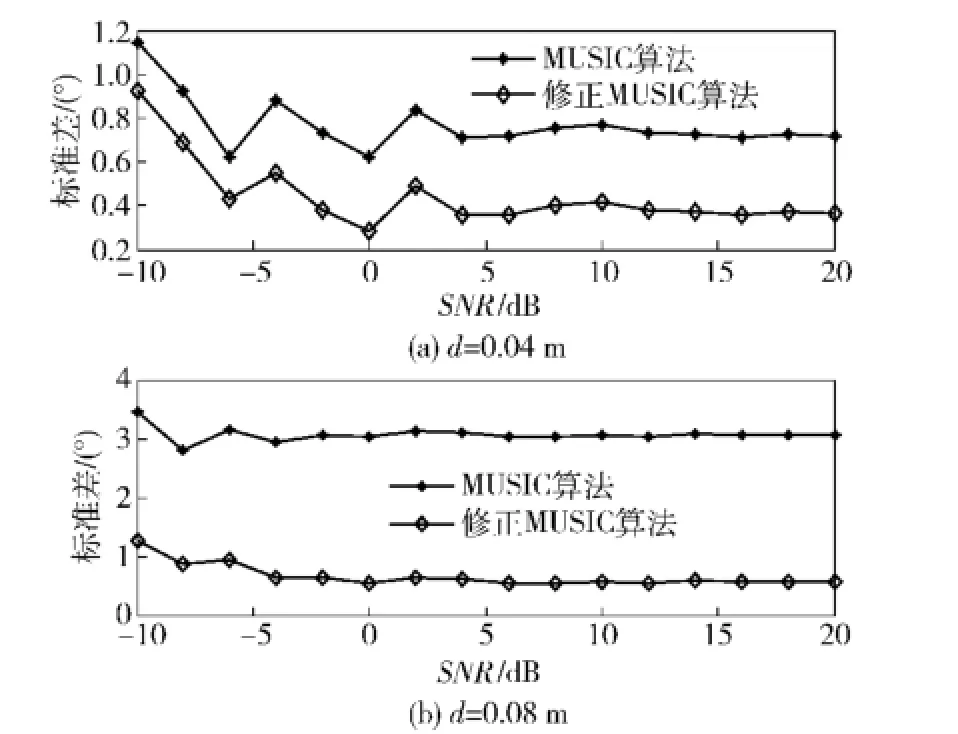
图5 不同信噪比情况下MUSIC算法DOA估计性能Fig.5 The performances of DOA estimation of MUSIC algorithms for different SNRs
5 压差型矢量水听器试验及结果分析
为了验证所提修正算法的有效性,处理了湖上试验数据。试验中目标信号为CW脉冲信号,压差型矢量水听器固定在接收船底部约2 m的深度,发射换能器悬挂在发射船底部约3 m的高度。发射船距离接收船约80 m远的距离,围绕接收船转动。发射信号中心频率为7 kHz,系统处理带宽为0.5 kHz,采样频率为50 kHz.
图6给出了压差矢量水听器4个阵元的信号波形。从图6中可看出,接收信号的信噪比很高,可近视认为纯信号。本试验系统中,压差矢量水听器的直径为0.08 m,对应的直径波长比约为0.373,不满足d≤0.2λ的工程近似条件。
图7给出了压差矢量水听器利用声强法进行DOA估计的结果。图7中“准确方位”为利用一个水听器阵列测定的方位值。复声强法表示利用(12)式计算的结果,修正声强法为利用(17)式计算的结果。由于声强法直接计算出目标的方位,所以历程图表现为一条曲线。从80 s的方位历程图中可以看出,修正声强法的估计曲线距离“准确方位”曲线更近,这说明其估计偏差小于复声强法。湖上实测数据的结果说明了修正声强法在实际系统中的有效性。

图7 声强法的方位历程图Fig.7 The time-DOA display of sound intensity methods
图8为利用MUSIC算法处理压差矢量水听器实测数据得到的方位历程图;图9为利用修正MUSIC算法处理压差矢量水听器实测数据得到的方位历程图(图中有几处不连贯,是因为数据文件中没有记录到完整的脉冲信号,剔除了一些这种不完整的数据文件)。通过对比可得出,修正MUSIC算法计算出的目标时间方位历程更加清晰、精细,这说明修正MUSIC算法相对于原MUSIC方法具有更好的DOA估计性能。湖上试验的结果充分验证了修正MUSIC算法在实际系统中的有效性。
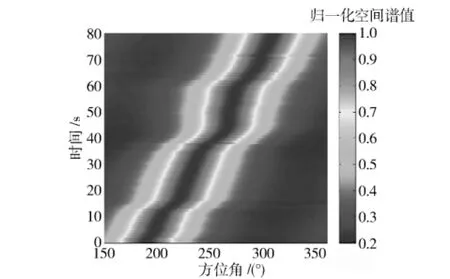
图8 单矢量水听器MUSIC算法的方位历程图Fig.8 The time-DOA display of MUSIC algorithm for single vector hydrophone

图9 单矢量水听器修正MUSIC算法的方位历程图Fig.9 The time-DOA display of modified MUSIC algorithm for single vector hydrophone
6 结论
在实际应用中,压差型矢量水听器要求直径波长比小于等于0.2,压差矢量水听器工作在高频段的时候,这一点很难满足,这会使矢量水听器的性能严重下降。针对上述问题,本文提出了一种修正的MUSIC算法,该方法通过修正矢量水听器输出的“阵列流型”,来改善单矢量水听器方位估计的性能。仿真实验和湖上试验数据处理结果表明:修正MUSIC算法在直径波长比大于0.2时依然能够获得与常规处理直径波长比小于0.2时相当的性能,因而该方法可以扩宽压差矢量水听器的工作频带,降低其应用成本,具有较大的工程应用价值。
References)
[1] 贾志富.全面感知水声信息的新传感器技术——矢量水听器及其应用[J].物理,2009,38(3):157-168.
JIA Zhi-fu.Novel sensor technology for comprehensive underwater acoustic information—vector hydrophones and their applications [J].Physics,2009,38(3):157-168.(in Chinese)
[2] 杨德森,洪连进.矢量水听器原理及应用引论[M].北京:科学出版社,2009.
YANG De-sen,HONG Lian-jin.Principle and application of the introduction of vector hydrophone[M].Beijing:Science Press, 2009.(in Chinese)
[3] 张李方,程锦房,何希盈.单矢量传感器信号处理方位估计[J].舰船科学技术,2009,31(3):104-107.
ZHANG Li-fang,CHENG Jin-fang,HE Xi-ying.Estimating the azimuth of signal processing using single vector-sensor[J].Ship Science and Technology,2009,31(3):104-107.(in Chinese)
[4] 惠俊英,惠娟.矢量声信号处理基础[M].北京:国防工业出版社,2009.
HUI Jun-ying,HUI Juan.Acoustic vector sensor signal processing [M].Beijing:National Defense Industry Press,2009.(in Chinese)
[5] 田坦.声纳技术[M].第2版.哈尔滨:哈尔滨工程大学出版社,2010.
TIAN Tan.Sonar technology[M].2nd ed.Harbin:Harbin Engineering University Press,2010.(in Chinese)
[6] 孙贵青,杨德森,张揽月,等.基于矢量水听器的最大似然比检测和最大似然方位估计[J].声学学报,2003,28(1):66-72.
SUN Gui-qing,YANG De-sen,ZHANG Lan-yue,et al.Maximum likelihood ratio detection and maximum likelihood DOA estimation based on the vector hydrophone[J].Acta Acustica, 2003,28(1):66-72.(in Chinese)
[7] 梁国龙,张铠,付进,等.单矢量水听器的高分辨方位估计应用研究[J].兵工学报,2011,32(8):986-990.
LIANG Guo-long,ZHANG Kai,FU Jin,et al.Research on highresolution direction-of-arrival estimation based on an acoustic vector-hydrophone[J].Acta Armamentarii,2011,32(8):986-990.(in Chinese)
[8] 陈羽,王伟,王建飞,等.噪声环境下单矢量水听器高分辨定向技术研究[J].哈尔滨工程大学学报,2013,34(1):1-5.
CHEN Yu,WANG Wei,WANG Jian-fei,et al.Research on high-resolution direction-of-arrival estimation of a vector hydrophone with noise[J].Journal of Harbin Engineering University, 2013,34(1):1-5.(in Chinese)
[9] 程彬彬.基于二维压差型压差型矢量水听器方位估计技术研究[D].西安:西北工业大学,2007.
CHENG Bin-bin.Studies on DOA estimation of two dimensional pressure-gradient vector transducer[D].Xi'an:Northwestern Polytechnical University,2007.(in Chinese)
[10] 杨德森,孙心毅,洪连进,等.基于矢量水听器的振速梯度水听器[J].哈尔滨工程大学学报,2013,34(1):7-14. YANG De-sen,SUN Xin-yi,HONG Lian-jin,et al.The velocity gradient sensor based on the vector sensor[J].Journal of Harbin Engineering University,2013,34(1):7-14.(in Chinese)
[11] 王永良,陈辉,彭应宁.空间谱估计理论与算法[M].北京:清华大学出版社,2004.
WANG Yong-liang,CHEN Hui,PENG Ying-ning.The theory and algorithms of spatial spectrum estimation[M].Beijing:Tsinghua University Press,2004.(in Chinese)
[12] 姚直象.基于多重信号分类法的一种声矢量阵方位估计算法[J].声学学报,2008,33(4):305-309.
YAO Zhi-xiang.A bearing estimation algorithm using an acoustic vector-sensor array based on MUSIC[J].Acta Acustica,2008, 33(4):305-309.(in Chinese)
[13] Hawkes M,Nehorai A.Acoustic vector-sensor correlations in ambient noise[J].IEEE Journal of Oceanic Engineering,2001, 26(3):337-347.
Optimization of Direction-of-arrival Estimation of Single Pressure Gradient Vector Hydrophone
WANG Xu-hu1,2,CHEN Jian-feng1,HAN Jing1,ZHANG Qun-fei1
(1.School of Marine Science and Technology,Northwestern Polytechnical University,Xi'an 710072,shaanxi,China;
2.College of Physics and Engineering,Qufu Normal University,Qufu 273165,Shandong,China)
The performance of direction-of-arrival(DOA)estimation of single pressure gradient vector hydrophone degrades rapidly when the diameter-wavelength ratio is more than 0.2.A modified MUSIC algorithm for single pressure gradient vector hydrophone is presented,which improves DOA estimation performance by optimizing the steering vector of the pressure gradient vector hydrophone.Simulation results indicate that the estimation performance of the MUSIC algorithm is better than that of the sound intensity method,and the modified MUSIC algorithm for single pressure gradient vector hydrophone has better estimation performance and robustness compared with MUSIC algorithm when the diameter-wavelength ratio is more than 0.2.The results of the lake trial powerfully testify the validity of the modified MUSIC algorithm for single pressure gradient vector hydrophone.
information processing;pressure gradient vector hydrophone;DOA estimation;MUSIC algorithm
��水听器信号波形 Fig.6 The
pulse signal of vector hydrophone
TB566
:A
1000-1093(2014)03-0340-07
10.3969/j.issn.1000-1093.2014.03.008
2013-01-25
国家自然科学基金项目(61001153);山东省高等学校科技计划项目(J09LG08);西北工业大学基础研究基金项目(JC20100223)
王绪虎(1979—),男,讲师,博士研究生。E-mail:xhwang@mail.nwpu.edu.cn;
陈建峰(1972—),男,教授,博士生导师。E-mail:chenjf@nwpu.edu.cn
