基于塔-索-拱建模的大跨钢管混凝土拱桥施工阶段动力特性研究

曾 勇，谭红梅

(1.重庆交通大学 山区桥梁与隧道工程省部共建国家重点实验室培育基地，重庆 400074；2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心，重庆 400074)

桥梁的自振特性包括自振频率与主振型，是进行结构动力分析和抗震设计的重要参数[1]。在施工阶段钢管混凝土拱桥进行动力特性研究，对大桥的抗震设计、抗风稳定性分析和施工监控等都有着重要的意义[2]。

黄福伟，等[3]和陈水盛，等[4]分析了影响钢管混凝土拱桥动力特性的敏感性因素，并进行了桥面系、横撑等对动力特性分析的影响分析。冯仲仁，等[5]和连岳泉，等[6]运用通用有限元软件ANSYS对某中承式异形钢管混凝土拱桥进行了动力特性的数值模拟分析，研究了拱肋、斜撑、倾角、二期恒载集度、边界条件等因素对拱桥动力特性的影响。孙昊，等[7]和黄小伟，等[8]的研究表明，矢跨比对拱桥面内振动影响很小，只是对面外振动有一定影响。这些研究大都针对成桥状态的钢管混凝土拱桥，对施工阶段的钢管混凝土拱桥的动力特性研究相对较少。为对施工阶段的钢管混凝土拱桥的设计与施工提供有效的理论支持，对其进行施工阶段的动力特性研究是十分必要的。

缆索吊装施工是大跨度拱桥的主要施工方法，扣索通过扣塔顶部的转索鞍直接锚固在锚碇上，扣塔只起竖向支撑作用，而不起水平支承作用。目前，许多缆索吊装施工的拱桥，如重庆菜园坝长江大桥、南宁永和大桥、合江长江一桥等。斜拉扣挂系统采用交换梁的方式，即扣索首先和扣索锚箱相连，然后通过扣塔横联钢管将荷载传到背索锚箱，背索锚再分散到锚碇。由于扣塔、扣索和拱肋之间存在耦合效应，扣塔的偏位会引起拱肋的变形，拱肋的变形也势必带动扣塔产生变形。在施工过程中，为了保证拱肋吊装安全，会控制扣塔与吊塔的塔顶偏位，往往只建扣索与裸拱，但这种建模方式不能真实反应结构的动力特性。因此，笔者针对合江长江一桥的斜拉扣挂系统跨度大、扣塔高度高、塔拱耦合强、横向刚度弱的特点，运用ANSYS分析软件进行(扣)塔-(扣)索-拱肋一体化建模的大跨度钢管混凝土拱桥施工阶段的动力特性研究，并与不考虑扣塔的(扣)索-拱肋建模进行了对比，以期对大跨度钢管混凝土拱桥的施工监控提出指导意见，从而达到指导实际工程的意义。

1 有限元计算方法

在桥梁结构的动力分析中，最基本的问题是结构的振动频率和振型。一般的结构运动方程为[1]：

(1)

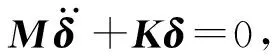
ANSYS 程序提供了7种计算结构的动力特性的方法[9]，分别为子空间法、分块Lanczos法、Power Dynamics 法、缩减法、非对称法、阻尼法和QR阻尼法。采用目前最有效的方法是子空间迭代法。动力特性计算过程中，考虑到自重的初始应力效应，因此在动力特性求解特征值的过程中，先静力分析，再将静力分析的应力刚度矩阵与结构原始刚度矩阵结合进行结构模态分析。

2 工程概况

合江长江一桥是主跨530 m的钢管混凝土中承式拱桥，为同类型桥梁之最。拱轴系数为1.45，净矢跨比为1/4.5。拱脚截面径向高度为16.0 m，拱顶截面径向高度为8.0 m；肋宽4.0 m，每条拱肋为上、下各两根φ1 320×22 mm、内灌C60混凝土的钢管混凝土弦杆；弦杆通过横联钢管φ762×16 mm和竖向两根φ660×12 mm钢管连接而构成钢管混凝土桁架[11]，见图1。扣塔构造立面见图2。

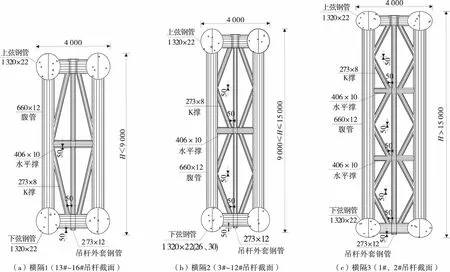
图1 拱肋构造截面Fig.1 Sectional view of arch ribs

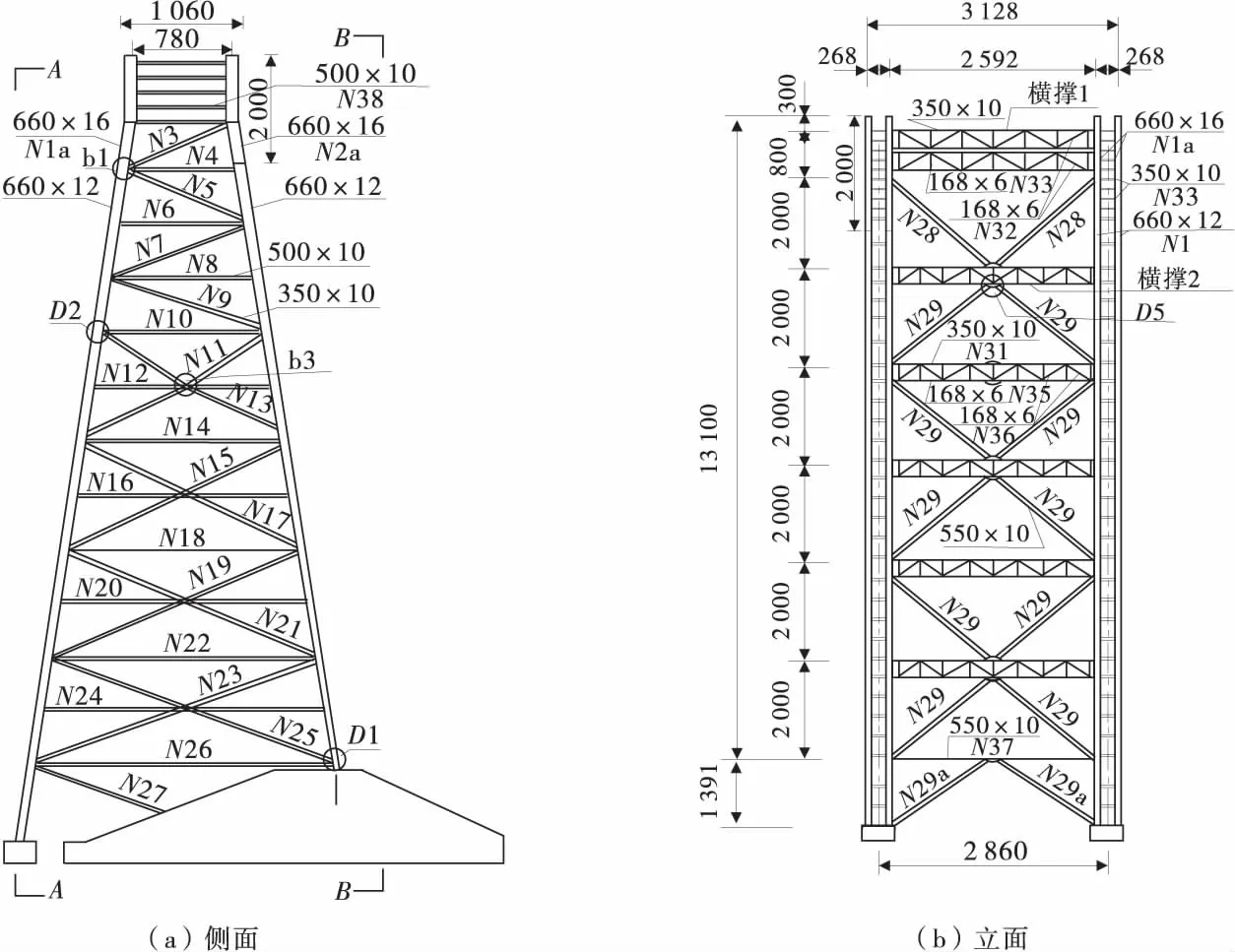
图2 扣塔构造立面Fig.2 Tower structures

大桥上部结构施工采用缆索吊装施工，主索跨径布置为430 m(重庆岸)+ 554 m(跨径)+ 405 m(宜宾岸)，塔架分别设置在两岸扣塔上，吊塔通过三角铰支承于扣塔顶部，两岸塔架顶高程相等，为407.800 m，塔高29.6 m(铰轴中心至塔顶索鞍轨道梁顶面高度)，塔顶离拱座顶面高度为168.1 m。重庆岸塔顶至地面高度为184.8 m，宜宾岸塔顶至地面高度为168.1 m。

主拱圈钢管桁架扣索体系由锚固点、张拉锚箱、扣塔、锚碇及扣索等5大部分组成。位于扣塔顶张拉端的锚箱由钢板与钢管组装焊接而成，并与扣塔组成共同受力的结构体系。扣塔分别位于两岸主拱座以内，重庆岸塔高分别为(131+13.91)m和宜宾岸为131 m，塔距为550.0 m，采用8φ660×12 mm钢管，主钢管内灌注C50混凝土，组成钢管混凝土格构柱扣塔，见图3。

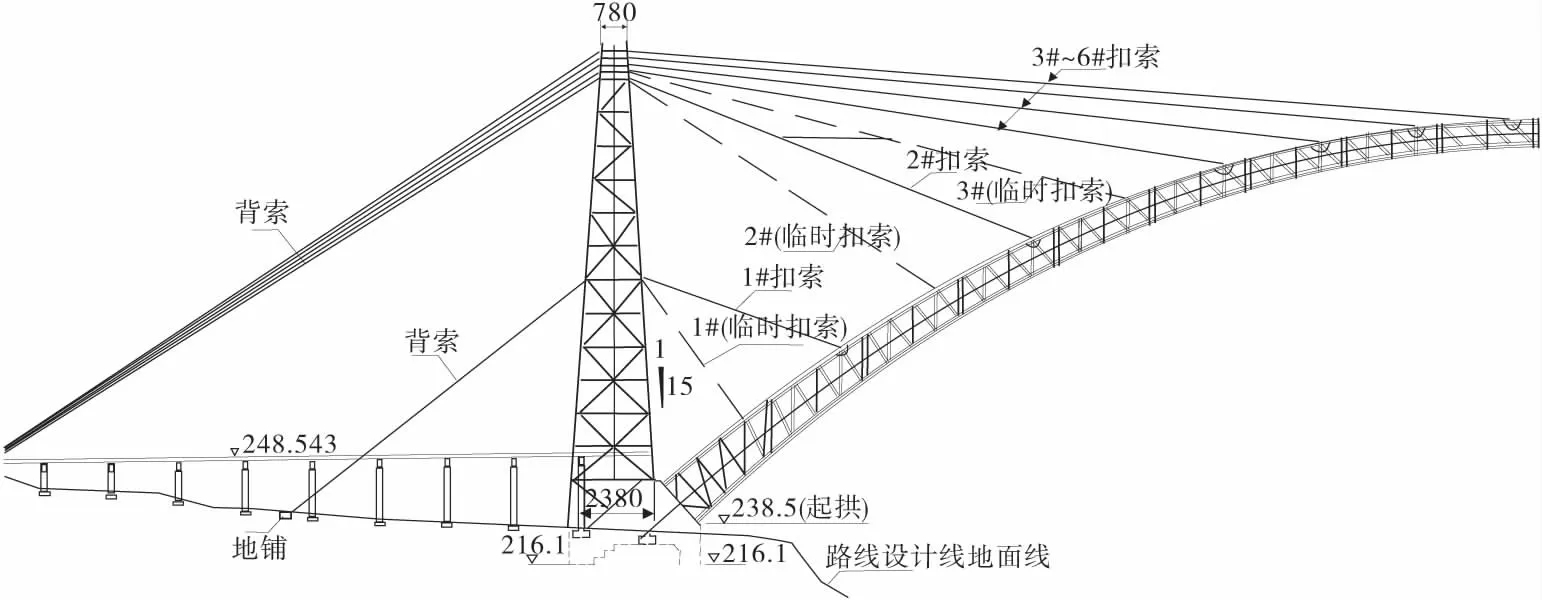
图3 合江长江一桥重庆侧的斜拉扣挂体系Fig.3 Elevation view of cable-stay system of Hejiang 1st Yangtze River Bridge at Chongqing side

3 建模思路

为了对比分析扣塔对最大悬臂阶段的合江长江一桥动力性能的影响，建立了两个有限元模型：塔-索-拱一体化建模的合江长江一桥(模型1)与不考虑扣塔的合江长江一桥的(模型2)，见图4。

图4 塔-索-拱一体化建模与不考虑扣塔的ANSYS模型Fig.4 Tower-cable-arch integration model and ANSYS modelwithout tower

有限元建模时，尽量精确考虑结构本身刚度和质量的分布，主拱和扣塔的截面采用与实际一致的形式。鉴于该桥在缆索吊装施工期间的构造特点，扣塔、拱肋采用三维梁单元模拟；扣索利用只考虑拉力的空间杆单元模拟，并计入其初始应变，不考虑拉索分段。有限元模型取塔-索-梁整体结构，扣塔全部构件采用Beam 188单元，索单元采用Link 10单元，拱肋构件采用Beam 188单元。扣塔的竖向主弦管为钢管混凝土构件，采用共节点的双单元模拟钢管与混凝土。无扣塔的模型(模型2)不考虑扣塔与备索的建模，扣索在端部按固结约束考虑。对于所取节段的边界条件的处理方法是：拱脚采用固结约束，拱顶不约束，扣塔底部采用固结约束。拉索分段对其主要频率相差很小，扣索的模拟一般都处理成一个索单元。

4 振型分析

通过对该桥3D模型的自振特性分析，得到桥梁前10阶自振频率及相应振型。最大悬臂状态下两个模型的前10阶频率(f1，f2)与相应的振型描述其振型以及频率对比见表1。

表1 模型1和模型2的频率与振型对比

从表1可以看出，两个模型前3阶的振型一致，分别为拱肋侧弯、拱肋竖弯、拱肋扭转。两个模型的主要基本振型的出现顺序一致，但是频率区别较大，拱肋的1阶竖弯频率相差最大，达到了27.9%。

限于篇幅，笔者只列出模型1的前10阶振型图，见图5。

图5 第1～10阶振型图(模型1)

从图5中可以看出，施工过程中最大悬臂阶段的大跨度钢管混凝土拱桥的振型比较复杂，具有以下特点：

1)主要振型包括拱肋面外、面内竖弯及扭转，扣塔的侧弯与扭转等模态，后面的振型趋于复杂。对于模型1，除了拱肋的振型外，还有扣塔的振型，以及拱肋与扣塔之间相互耦合的振型。

2)模型1的第1阶振型为拱肋横向侧弯模态，基频为0.150，模型2基频的为0.168，表明钢管混凝土拱桥的横桥向刚度很弱。拱肋的竖向刚度大于其横向刚度，面外的稳定问题突出，考虑扣塔后基频降低了12%。

3) 模型1与模型2的前3阶振型相同，分别为拱肋1阶侧弯、拱肋1阶竖弯和拱肋1阶扭转。从这一点来看，不考虑扣塔建模的模型2在一定程度上能够反应结构的低阶基本振型，但两种模型的低阶基本振型的频率有不同程度的差别。

4)模型1的第4阶振型为扣塔的横桥向振型，第8阶为扣塔的扭转振型。在扣索的作用下，扣塔的纵桥向振型受到了抑制。扣塔的横桥向刚度大于扭转刚度，但扣塔的横桥向刚度还是大于最大悬臂阶段拱肋的横桥向刚度。

5)施工过程中钢管混凝土拱桥结构的杆件多，构造复杂，高阶振型复杂，往往是扣塔与拱肋的耦合振型。因为跨度大的缘故，无论是模型1还是模型2，该上承式钢管混凝土拱桥最大悬臂阶段的基频均较小，结构的横向风敏感性突出。

两个模型前500阶振型的频率见图6。

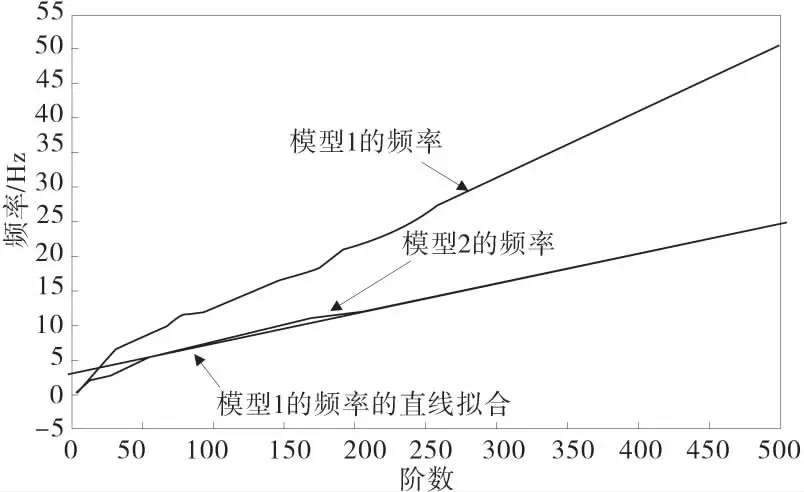
图6 模型1与模型2的第500阶频率Fig.6 The 500th order frequency of model 1 and model 2

从图6可以看出，大致以第30阶振型为界，1～30阶的振型接近一条直线；30阶以后的振型又是接近一条直线，但两条直线的斜率不同。模型2的频率要高于模型1的频率，且振型越高，频率相差越大。

为了研究扣索与背索索力对结构振型的变化规律，在模型1中考虑5种工况来分析前10阶振动频率的影响规律，计算工况如下。

工况1： 2倍背索索力；

工况2： 2倍扣索索力；

工况3： 同时2倍背索与扣索索力；

工况4： 同时1.5倍背索与扣索索力；

工况5： 同时1.2倍背索与扣索索力。

扣索与背索索力对结构的振型没有影响，但改变自振频率。无论是增加扣索索力还是背索索力，均降低了结构1阶对称侧弯、1阶反对称竖弯与1阶扭转振动的振动频率，但降低不多，同时增加了扣塔的第1阶横向振动频率。5个工况对第9阶振型(拱肋3阶侧弯)的自振频率影响较大，计算结果见图7。

图7 模型1的背、扣索索力变化的影响Fig.7 Influence of cable force change of model 1

5 结 论

通过对大跨度钢管混凝土拱桥缆索吊装施工过程中的扣塔-扣索-拱肋一体化建模最大悬臂状态动力特性的研究，得到如下结论：

1)大跨度钢管混凝土拱桥缆索吊装施工过程的最大悬臂阶段，其扣塔、扣索和拱肋之间存在耦合效应，只有塔-索-拱一体化建模才能更真实地反应大跨度钢管混凝土拱桥施工阶段的动力特性。

2)塔-索-拱肋一体化建模的最大悬臂施工阶段大跨度钢管混凝土拱桥的建模方式更接近工程实际，主要振型包括拱肋面外、面内竖弯及扭转、扣塔的侧弯与扭转等，高阶振型复杂，拱肋与扣塔相互耦合。不考虑扣塔建模的有限元模型在一定程度上能够反应结构的低阶基本振型，但其频率有不同程度的差别。

3)大跨度钢管混凝土拱桥施工节段的横桥向刚度很弱，面外的稳定问题突出，结构的风敏感性更为突出。考虑扣塔建模后，基频降了12%。扣塔的纵桥向振型受到了扣索的抑制。扣塔的横桥向刚度大于其扭转刚度，但扣塔的横桥向刚度还是大于最大悬臂阶段拱肋的横桥向刚度。

4)有趣的是，无论是模型1还是模型2， 30阶后的频率接近一条直线，主要原因是扣塔与拱肋杆件较多的缘故。背、扣索索力的变化对全桥结构的振型影响较小，但在一定程度上改变自振频率。

[1] 项海帆,刘光栋.拱结构的稳定与振动[M].北京:人民交通出版社,1991.

Xiang Haifan,Liu Guangdong.Stability and Vibration of Arch Structures [M].Beijing:China Communications Press,1991.

[2] 陈宝春.钢管混凝土拱桥[M].北京:人民交通出版社,2007.

Chen Baochun.Concrete-Filled Steel-Tube Arch Bridges [M].Beijing:China Communications Press,2000.

[3] 黄福伟,刘怀林.中承式钢管混凝土拱桥动力特性分析[J].哈尔滨工业大学学报,2003,30(增刊1):255-258.

Huang fuwei,Liu huailin.Analysis of dynamic characteristics of half-through CFST arch bridges [J].Journal of Harbin Institute of Technology,2003,35(S1):255-258.

[4] 陈水盛,陈宝春.钢管混凝土拱桥动力特性分析[J].公路,2001(2):10-14.

Chen Shuisheng,Chen Baochun.Analysis of dynamic characteristics of concrete filled steel tubular arch bridge [J].Highway,2001(2):10-14.

[5] 冯仲仁,李彩霞,吴刚刚.下承式钢管混凝土拱桥自振特性的有限元分析[J].武汉理工大学学报,2005,27(7):50-53.

Feng Zhongren,Li Caixia,Wu Ganggang.Finite element analysis on through concrete-filled steel-tabular arch bridge’s self-vibration characteristics [J].Journal of Wuhan University of Technology,2005,27(7):50-53.

[6] 连岳泉,梁群.单拱肋外倾式钢管混凝土拱桥动力特性分析[J].武汉理工大学学报:交通科学与工程版,2012,36(5):984-987,991.

Lian Yuequan,Liang Qun.Dynamic characteristics analysis of extroversion CFST arch bridge with single rib [J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2012,36(5):984-987,991.

[7] 孙昊,钱永久,蔡迎春.结构参数变化对钢管混凝土拱桥动力特性的影响分析[J].重庆交通大学学报:自然科学版,2009,28(6):982- 985,1074.

Sun Hao,Qian Yongjiu,Cai Yingchun.Influence of structural parameters variation on dynamic characteristics of concrete filled steel tubular arch bridge [J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(6):982-985,1074.

[8] 黄小伟,王浩,李爱群,等.中承式异形钢管混凝土拱桥动力特性分析[J].建筑科学与工程学报,2012,29(5):88-93.

Huang Xiaowei,Wang Hao,Li Aiqun,et al.Analysis on dynamic characteristics of half-through special-shaped CFST arch bridge [J].Journal of Architecture and Civil Engineering,2012,29(5):88-93.

[9] 龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社,2004.

Gong Shuguang,Xie Guilan.ANSYS Command and Parameter Programming [M].Beijing:China Machine Press,2004.