简支单箱双室梯形结合梁的畸变效应研究

张彦玲，侯忠明，李运生，刘沛叶

(1.石家庄铁道大学 土木学院，河北 石家庄 050043; 2. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043; 3. 清华大学 土木水利学院，北京 100084)

钢-混凝土箱形结合梁在中等跨径桥梁，尤其是平曲线桥梁中应用非常广泛，但由于曲线结合箱梁截面存在弯曲、扭转、畸变、及剪力滞等综合效应，使其受力十分复杂。

在正常使用荷载作用下，可通过荷载分解法，将梁轴曲率的影响或偏心竖向荷载分解为弯曲荷载和扭转荷载的组合，其中扭转荷载又可分解为刚性周边不变形的扭转荷载和自相平衡的畸变荷载。H. Nakai，等[1]和Fan Zhanfei，等[2]分别给出了单箱单室矩形和梯形截面偏心竖向荷载的分解方法；P.Nam-Hoi，等[3]和李运生，等[4]分别给出了单箱双室及多室矩形和梯形截面偏心竖向荷载的分解方法。完成荷载分解后，即可以在各荷载分量的单独作用下进行箱梁结构的独立分析，笔者专门针对其畸变效应进行分析。

控制箱梁畸变变形的有效方法是沿跨度方向设置一定数量的横隔板[5-6]。关于单箱单室箱型截面的畸变效应研究已有很多报道，由于截面构造相对简单，常采用解析法[7-8]、弹性地基梁法[9-10]或有限元法[11-12]进行分析，但对于单箱双室截面，目前的相关研究还较少。

笔者针对钢-混凝土单箱双室结合梁，在荷载分解的基础上，对其畸变变形机理进行研究，分析横隔板对单箱双室结合梁畸变效应的影响，并针对结合梁的特点，对柔性连接件导致的结合面相对滑移对畸变效应的影响进行分析。

1 单箱双室结合梁畸变荷载的分解

笔者在文献[4]中给出了单箱双室梯形结合梁偏心竖向荷载的分解方法，单箱双室对称截面在任意位置的偏心竖向荷载作用下，可分解为弯曲荷载、刚性扭转荷载和畸变荷载，其中畸变荷载又可分解为第一畸变荷载和第二畸变荷载，如图1。

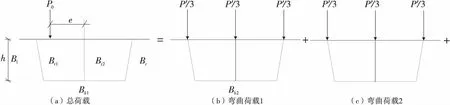
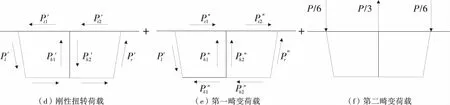
P0—任意竖向荷载；e—偏心距；h—上板中心到下板中心的距离；Bti，Bbi，Bl，Br—板块宽度或长度，

图1(d)中的刚性扭转荷载为：

图1(e)中的第一畸变荷载为：

2 单箱双室结合梁畸变效应分析

2.1 工程背景及有限元模型

以哈大客运专线中的简支钢-混凝土结合梁桥为工程背景。该结合梁为跨度23.6 m的单箱双室梯形截面梁，钢梁采用Q370qE，桥面板采用C50无收缩混凝土，底板铺200 mm厚C30素纤维混凝土。钢箱梁与混凝土板之间的抗剪连接件采用直径22 mm圆头栓钉进行连接。结合梁横截面尺寸如图2。

图2 结合梁横断面Fig.2 Cross-sections of composite beam

选取跨中截面为计算截面，采用ANSYS软件建立有限元模型，混凝土采用SOLID65实体单元，钢梁及横隔板均采用SHELL43壳单元，不考虑钢梁与混凝土板之间相对滑移，在二者相应节点处进行完全耦合。整个有限元模型划分15 507个单元，19 079个节点。边界条件采用简支，在一端的支座中心线位置将钢梁底板的纵向、竖向和横向线位移全部约束，另一端支座中心线位置则只将钢梁底板的竖向和横向线位移约束。为了能够更清楚地分析畸变变形，不考虑结合梁底板混凝土层的影响。

该铁路结合梁为双线结合梁，各线路中心距梁截面中心2.5 m。在有限元模型中在一侧线路中心位置，即距横截面中心线2.5 m处的跨中顶面施加P=1 000 kN的偏心集中荷载，此时其截面应力仍处于弹性范围内。根据第1节给出的荷载分解方法，将施加的集中荷载分解为弯曲荷载、刚性扭转荷载、第一和第二畸变荷载，在两种畸变荷载下进行结合梁畸变效应的分析。为了加强截面的整体刚度，沿梁轴方向设置了厚度为25 mm的钢横隔板。根据横隔板数量的不同，分为4种不同的工况模型：

1)无隔板工况：全梁不布置横隔板；

2)两隔板工况：只在梁端处布置两道端横隔板；

3)三隔板工况：在两个梁端及跨中布置横隔板；

4)五隔板工况：在两个梁端、跨中及L/4、3L/4处布置横隔板。

2.2 畸变变形云图

各种横隔板工况下单箱双室结合梁在第一和第二畸变荷载分量作用下的变形云图见图3。

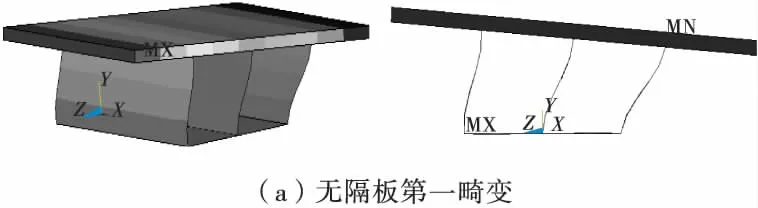
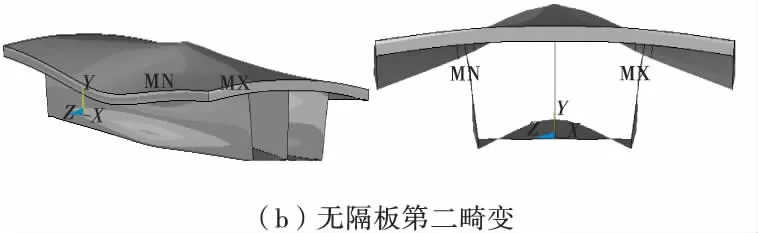
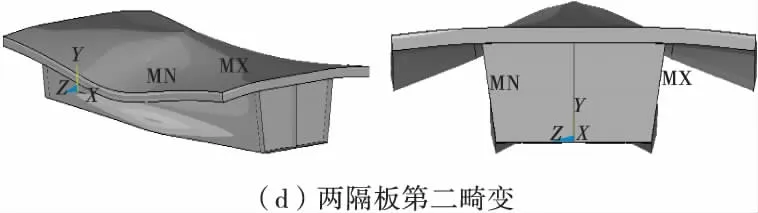
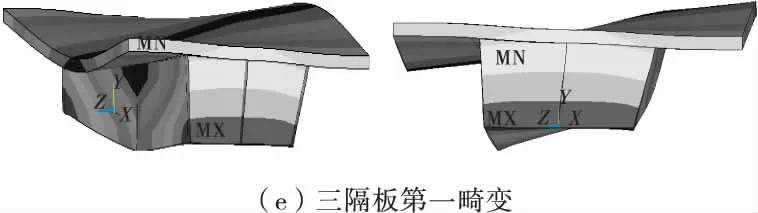
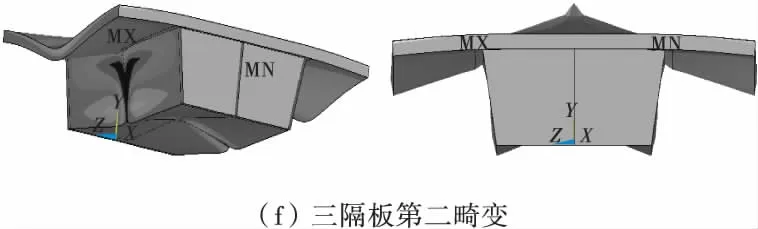
图3 结合箱梁的畸变变形Fig.3 Distortional deformation of combined box beam

由图3可以看出：

1)单箱双室箱型结合梁的第一畸变变形和第二畸变变形形式不同，第一畸变变形是将双室作为一个整体，在整个箱型截面上发生畸变变形，为反对称变形；第二畸变变形为两室各自向中间腹板处发生畸变，为横截面上的正对称变形。

2)无隔板工况下，结合梁全梁变形比较均匀，无突变位置，在第一畸变荷载作用下，只在钢腹板处发生横向变形，混凝土板则发生横移和偏转，本身没有弯曲变形；在第二畸变荷载作用下，在跨中集中偏心荷载位置畸变变形最大，混凝土板和钢梁底板均出现横向对称上拱现象。

3)两隔板工况下，端部横隔板使该处截面的第一畸变变形明显减小，此时结合梁全梁变形不再均匀，在跨中集中偏心荷载位置变形较大；第二畸变变形则与无横隔板时形状相同。

4)三隔板及五隔板工况下，在跨中位置第一畸变变形均明显减小，但第二畸变变形形状与无中横隔板时基本相同。

2.3 截面畸变角

为了更清楚地分析结合箱梁的畸变变形，可将图4的箱型截面下翼缘角点2的畸变角作为参数进行分析。

将图4中钢梁上翼缘角点1和下翼缘角点2的横向位移差值除以两点之间的竖向距离，将下翼缘角点2和中间腹板处下翼缘角点3的竖向位移差值除以两点之间的水平距离，二者结果进行叠加，可近似得到各截面下翼缘角点2处的第一畸变角和第二畸变角，如图5和图6。

由图5可知：

1)无隔板时沿跨度方向各截面的第一畸变角远远大于两隔板工况和其它工况，说明端横隔板对减小结合箱梁的畸变变形作用显著；

2)两隔板时，沿跨度方向各截面的第一畸变角比设有中横隔板的其它工况明显偏大，说明中间横隔板进一步明显减小了截面的畸变变形；

3)五隔板工况与三隔板工况相比，1/4跨的两个中横隔板可减小第一畸变变形，但总体来说沿跨度方向各截面的第一畸变角差别较小，说明设两道端横隔板和一个跨中横隔板作用效果最好。

由图6可以看出：

1)无隔板和两隔板工况下各截面的第二畸变角基本相同，说明端横隔板对减小第二畸变变形作用较小；

2)五隔板和三隔板工况相比，中横隔板所在位置第二畸变变形减小，但总体差别不大；

3)无、两隔板工况的第二畸变角明显大于后三、五隔板工况，说明跨中横隔板对减小第二畸变角效果明显。

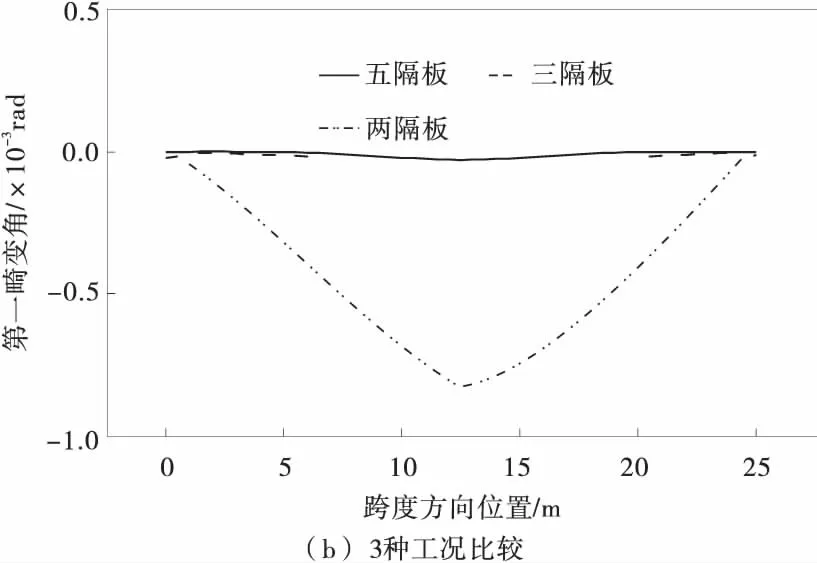
图5 第一畸变荷载作用下的畸变角Fig.5 Distortion angle under the first distortion load

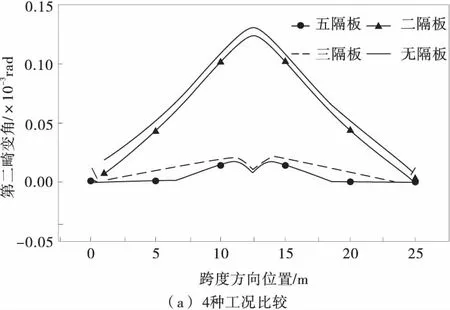
图6 第二畸变荷载作用下的畸变角Fig.6 Distortion angle under the second distortion load

2.4 畸变翘曲应力

选取包含钢梁下翼缘角点2的腹板单元，将每个板单元4个节点的平均应力作为单元应力，得到各单元在第一畸变荷载作用下的纵向翘曲应力沿梁轴的分布如图7。

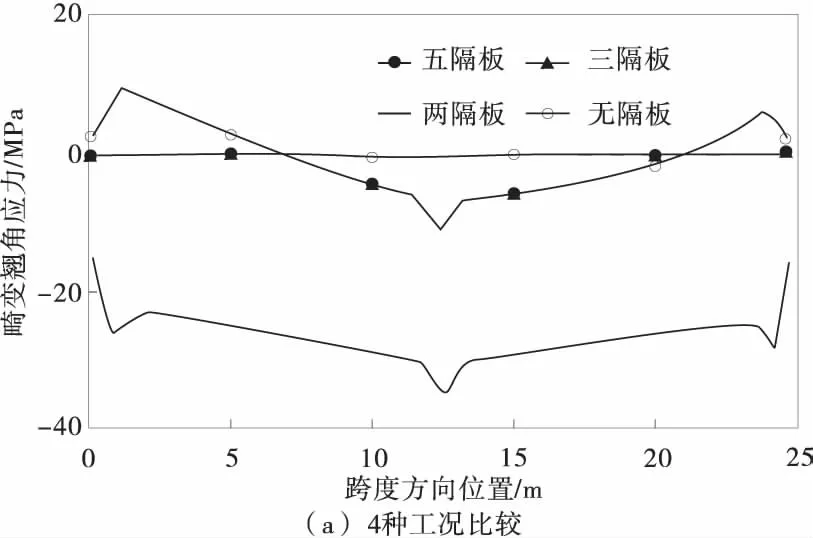
图7 第一畸变荷载作用下的畸变翘曲应力Fig.7 Distortion warping stress under the first distortion load

由图7可知：

1)无隔板时，除在跨中集中荷载处有较大应力外，第一畸变翘曲应力沿跨度方向分布比较均匀，由于截面整体抗扭刚度小，应力值远远大于其它工况，只有在梁端迅速减小，由于是单元平均应力，所以未减小至0。

2)两隔板时，梁端横隔板对于畸变变形起到较强的约束作用，相当于畸变变形的抗扭支承，因此在梁端横隔板附近出现应力集中现象，且方向与跨中畸变翘曲应力相反。

3)与只设有端横隔板的两隔板工况相比，设有跨中横隔板的三隔板和五隔板工况，其畸变翘曲应力沿整个跨度方向均明显减小。三隔板工况下跨中位置第一畸变翘曲应力比两隔板工况减小90.7%，五隔板工况则减小98.5%，由此可见中间横隔板对减小组合箱梁的显著作用。

4)三隔板工况与五隔板工况下第一畸变翘曲应力差别不大。与三隔板工况相比，五隔板工况下1/4跨的横隔板加强了对截面畸变变形的约束作用，在横隔板存在的位置均出现了应力集中，从总体水平上反而比三隔板工况下的翘曲应力略有增大。

在第二畸变荷载作用下，各单元的纵向翘曲应力沿梁轴的分布如图8。

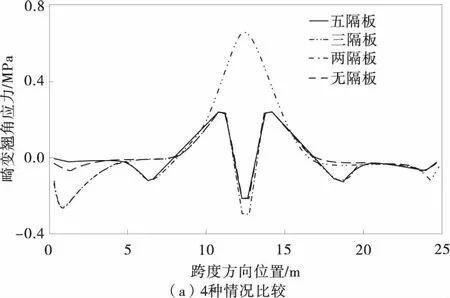
图8 第二畸变荷载作用下的畸变翘曲应力Fig.8 Distortion warping stress under the second distortion load

由图8可知：

1)与第一畸变翘曲应力相比，第二畸变翘曲应力值较小，且各工况之间的应力差值也没有第一畸变荷载下明显。

2)无中横隔板的无隔板和两隔板工况，其纵向翘曲应力差别很小，说明端横隔板对第二畸变翘曲应力无影响；有中横隔板的三隔板和五隔板工况，翘曲应力在中横隔板位置均发生了明显的降低，这是由于第二畸变变形为横截面对称变形，此时中横隔板发生面内弯曲，而其较大的抗弯刚度有效降低了该处的畸变应力和畸变变形。

2.5 结合面相对滑移对畸变效应的影响

以上分析中，在有限元模型中均将钢梁与混凝土板之间的相应节点在梁轴纵向、截面横向和竖向全部耦合，未考虑钢梁与混凝土板之间相对滑移，但由于栓钉连接件本身的柔性，即使在完全连接的结合梁中，结合面的相对滑移也是不可避免的。本节讨论相对滑移对单箱双室结合箱梁畸变效应的影响。

将有限元模型中钢梁与混凝土板之间的相应节点在梁轴纵向和截面横向的耦合解除，采用栓钉的实常数对其滑移曲线进行定义，以考虑在这两个方向上的相对滑移。由于一般钢梁与混凝土板之间的竖向掀起变形很小，所以竖向耦合没有解除。栓钉的滑移曲线可按式(1)进行定义[13]：

(1)

式中：V为栓钉所受剪力；ξ为V作用下在钢梁与混凝土结合面上产生的滑移；α，β为计算参数，可根据文献[14]取为α=0.7，β=0.8；Vu为单个栓钉的抗剪承载力，计算中取：

(2)

式中：Ast为栓钉的截面面积；fc为混凝土轴心抗压强度；fstu为栓钉采用的极限抗拉强度。

考虑结合面相对滑移后得到的钢梁下翼缘角点2沿梁轴方向的畸变应力及变形见图9。

图9 结合面相对滑移对畸变效应的影响Fig.9 The effect of relative slip at the bond surface on distortional effect

由图9可知：

与不考虑滑移的情况相比，钢梁与混凝土板之间的相对滑移使结合箱梁的畸变应力和畸变变形均有所增大，跨中截面的第一畸变应力增大26%，第二畸变应力增大25.8%；第一畸变角增大17.8%，第二畸变角虽然在跨中截面有所减小，但在跨中截面附近增幅达到22.5%。这说明结合面相对滑移使结合梁截面的畸变翘曲刚度减小，畸变应力和畸变变形增大，且增加幅度较大，在畸变效应计算时应考虑柔性栓钉引起的结合面相对滑移影响。

3 结 论

1) 单箱双室箱型结合梁的畸变变形可分解为第一畸变变形和第二畸变变形，其中第一畸变变形为整个箱型截面上的反对称变形，且为主要畸变变形，第二畸变变形为横截面上的正对称变形；

2) 端横隔板对减小单箱双室结合箱梁的第一畸变变形和第一畸变应力作用显著，但对第二畸变变形和第二畸变应力基本无影响；

3) 中横隔板对减小第一畸变变形和应力及第二畸变变形和应力均作用显著，但设置跨中横隔板后，再增加其它横隔板，对畸变效应的减小作用不再明显；

4) 由柔性栓钉连接件造成的结合面相对滑移减小了结合梁截面的畸变翘曲刚度，使畸变应力和畸变变形明显增大，因此其对单箱双室结合箱梁畸变效应的影响不容忽视。

[1] Nakai H,Yoo C H.Analysis and Design of Curved Steel Bridges [M].New York:McGraw-Hill,1988.

[2] Fan Zhanfei,Helwig T A.Distortional loads and brace forces in steel box girders [J].Journal of Structural Engineering,2002,128(6):710-718.

[3] Nam-Hoi P,Choi Sanghyun,Kang Young-Jong.Exact distortional behavior and practical distortional analysis of multi-cell box girders using an expanded method [J].Computers and Structures,2005,83(19/20):1607-1626.

[4] 李运生,刘沛叶,张彦玲.弹性阶段单箱双室梯形结合梁弯扭效应分析[J].广西大学学报:自然科学版,2013,38(1):92-99.

Li Yunsheng,Liu Peiye,Zhang Yanling.Bending-torsion effect analysis of trapezoidal single box-double cell composite beams in elastic stage [J].Journal of Guangxi University:Natural Science,2013,38(1):92-99.

[5] 刘小渝,孙童龄.横隔板对钢箱梁受力畸变的分析[J].重庆交通大学学报：自然科学版,2007,26(5):9-12.

Liu Xiaoyu,Sun Tongling.Effect of diaphragm on distortion of steel box girder [J].Journal of Chongqing Jiaotong University:Natural Science,2007,26(5):9-12.

[6] 张长青，安永日，安里鹏.组合结构箱梁扭转极限承载力计算方法研究[J].重庆交通大学学报：自然科学版,2011,30(3):369-371.

Zhang Changqing,An Yongri,An Lipeng.Study on calculation method of ultimate strength of torsional moment of composite steel box girders [J].Journal of Chongqing Jiaotong University:Natural Science,2011,30(3):369-371.

[7] 王银辉,陈山林,钱立.考虑形心和剪心分离的变曲率箱梁弯扭分析[J].重庆建筑大学学报,2007,29(3):66-69.

Wang Yinhui,Chen Shanlin,Qian Li.Flexure-torsion analysis of

variable-curvature-box girder considering non-coincidence of torsion center and gravity center [J].Journal of Chongqing Jianzhu University,2007,29(3):66-69.

[8] Yu A M,Yang J W,Nie G H,et al.An improved model for naturally curved and twisted composite beams with closed thin-walled sections [J].Composite Structures,2011,93(9):2322-2329.

[9] 杨丙文,黎雅乐,万水,等.波形钢腹板箱梁畸变应力分析[J].东南大学学报:自然科学版,2011,41(5):1065-1069.

Yang Bingwen,Li Yale,Wan Shui,et al.Stress analysis of box girders with corrugate steel webs under distortion [J].Journal of Southeast University:Natural Science,2011,41(5):1065-1069.

[10] Yao T H,Fu C C.Application of EBEF method for the distortional analysis of steel box girder bridge superstructures during construction [J].Advances in Structural Engineering,2002,5(4):211-221.

[11] 卢彭真,魏召兰,占玉林,等.基于位移场的薄壁箱梁结构约束扭转和畸变效应分析[J].四川大学学报:工程科学版,2009,41(1):74-79.

Lu Pengzhen,Wei Shaolan,Zhan Yulin,et al.Analysis of restrained torsion and distortion effect for thin-walled box girder structure based on displacement field [J].Journal of Sichuan University:Engineering Science,2009,41(1):74-79.

[12] Ramos O R,Schanack F,Ortega G,et al.Unusual structural effects in a variable-depth box girder bridge:the Pujayo viaduct [J].Engineering Structures,2011,33(2):615-620.

[13] 张彦玲.钢-混凝土组合梁负弯矩区受力性能及开裂控制的试验及理论研究[D].北京:北京交通大学,2009:20-48.

Zhang Yanling.Theoretical and Experimental Research of Stress Performance and the Crack Control of Steel-Concrete Composite Beams under Negative Moment Zone [D].Beijing:Beijing Jiaotong University,2009:20-48.

[14] 聂建国,田春雨.简支组合梁板体系有效宽度分析[J].土木工程学报,2005,38(2):8-12.

Nie Jianguo,Tian Chunyu.Effective widths of simply supported composite beams with transverse end girders [J].China Civil Engineering Journal,2005,38(2):8-12.