自锚式悬索桥主缆下料长度精细化计算

韩旭辉，袁阳光，陈安洋，赵建峰，舒 涛

(1.山西交通职业技术学院，山西 太原 030000；2.长安大学 公路学院，陕西 西安 710064)

自锚式悬索桥主缆的下料长度是影响结构成桥精度的关键参数，精确计算主缆下料长度是保证悬索桥结构成桥后几何线形满足设计要求的必要条件，也是施工控制的第一步。目前，研究悬索桥的理论线形(由悬索桥的几个关键点决定，不包括索鞍位置线形修正)计算方法较多。潘永仁，等[1]在已有悬索桥分析理论[2]的基础上采用悬链线单元建立几何非线性有限元方程，通过多次迭代[3]得到成桥状态结构的真实几何形状及内力。文曙东，等[4]基于分段悬链线理论研究了自锚式悬索桥线形精确计算方法。同时，经过国内学者们多年的研究，在悬索桥索鞍位置及纵向曲线设计方法方面也取得了较多的研究成果。唐茂林，等[5]研究了单一半径圆弧索鞍位置设计；李传习，等[6]提出了悬索桥索鞍位置的分离计算方法；魏建东，等[7]研究了悬索桥鞍槽纵向曲线设计方法，并对每种鞍座的设计建立了相应的高效作图法。基于上述研究成果，主缆中心索股无应力长度计算也具有较高精度。

考虑到实际主缆为空间结构物，主缆各索股空间分布位置存在差异，特别对于主索鞍及锚固端位置主缆，主索鞍处以圆曲线通过鞍体，各层索股圆曲线半径差异较大，锚固区段主缆一般采用分层分散的方式锚固，每根索股锚固位置坐标不同，相应主缆各索股的无应力长度不一致，因此有必要对主缆下料长度作精细化计算修正后给出。笔者考虑自锚式悬索桥梁端锚固面为平面，主索鞍为一般单圆曲线设计，给出了基于中心索股无应力长度主缆下料长度精细化计算方法。

1 计算假定

计算方法考虑以下基本假定：

1)主缆为理想柔性材料，既不受压也不受弯；

2)主缆横截面积在外荷载作用下变化微小，忽略不计；

3)主缆材料满足胡克定律，应力与应变呈线性关系。

2 精确计算中心索股无应力长度

悬链线单元模拟主缆[8]，对主缆单元进行离散，除索鞍过渡段，其它位置主缆均离散为悬链线，累计各个悬链线单元的无应力长度，再加上鞍座位置主缆圆弧段无应力长度，即可得到主缆中心索股准确下料长度。

3 各索股下料长度精细化修正计算

3.1 瞄固区修正计算(散索鞍→锚垫板区段)

图1为梁端锚固区立面图，A-A断面为展索断面，B-B断面为锚固断面。将展索点与锚固点之间主缆悬链线段简化为直线段，并建立图2中的锚固端简化空间直角坐标系，设计展索中心点A点坐标为(x1,0,z1)，锚端中心点B点坐标为(x2,0,z2)，由A、B两点坐标可求得锚固区主缆中心索股有应力长度L，与水平向夹角θ；A，B点坐标转换为相对坐标表达即A(0,0,0)，B(-Lcosθ,0,-Lsinθ)。

图1 锚固端立面Fig.1 Elevation view of anchor end

图2 锚固端简化坐标系Fig.2 Simplified coordinate system of anchored end

图3 A-A断面局部坐标系Fig.3 Local coordinate system of A-A cross section

图4 B-B断面局部坐标系Fig.4 Local coordinate system of B-B cross section

将上述i点及j坐标换算至图1整体坐标系下，得到其换算坐标：

i点坐标：(-zisinθ,-yi,zicosθ)；

j点坐标：(-zjsinθ-Lcosθ,-yj,zjcosθ-Lsinθ)。

i，j点形成Ⅰ象限(其它象限计算方法相同)任意索股单元，相应其有应力长度为：

综上所述，通过建立主缆锚端局部坐标系，按空间坐标变换方法，统一至整体坐标系下即可确定任意索股两端相对位置坐标，进而较精确求得锚固段主缆各索股修正无应力长度。

3.2 主索鞍位置修正计算

由于主索鞍空间构造复杂，无法在程序中精确模拟，故需在理论成桥状态基础上按照索鞍及主缆实际尺寸对主缆进行必要的修正，以减小主缆制造误差，保证成桥精度。主缆线形一经确定，按前述已有研究成果即可确定索鞍位置及中边跨主缆的入鞍角φ1，φ2(图5)，进而确定鞍体内圆弧段主缆的有应力长度，可据此反算无应力长度。

图5 索鞍位置局部放大Fig.5 Partial enlargement drawing of cable saddle

从图5可以看出主缆以圆弧形式通过塔顶，各层主缆在塔顶处圆弧半径不同，因此需要计算各层索股的圆弧半径Ri并基于此对各层索股无应力长度作精细化修正。

式中:d为构造尺寸；m为相对中心索股的层数，位于中心索股上即为正，反之为负；R为主缆中心索股曲线半径；T1及T2分别为索鞍边中跨主缆的拉力；E为主缆弹性模量；A为主缆断面面积。

4 自锚式悬索桥工程算例

4.1 算例描述

以一座跨径布置为(45 m+120 m+45 m)的自锚式悬索桥为工程实例对上述精细化计算方法进行验证。图6为理想成桥状态结构成桥计算模型，拉索采用悬链线索单元模拟，塔顶索鞍位置处水平约束释放，主缆面积A=0.065 993 m2,弹性模量E=20 500 MPa，塔顶主索鞍以单圆曲线过渡，边跨入鞍角φ1=39.986 8°,中跨入鞍角φ2=34.901 6°，索鞍左主缆内力T1=33 085 kN，索鞍右主缆内力T2=30 908 kN，中心索股圆曲线半径R=3.10 m，锚固端主缆内力28 974 kN，主缆中心索股有应力长度S=9.969 5 m，与水平向夹角θ=29.018 3°;主缆索股布置及编号如图7，上述A-A断面a=55.8 mm，b=48.3 mm，B-B断面c=350 mm，塔顶主缆断面d=49 mm。

图6 自锚式悬索桥有限元计算模型Fig.6 FE model for the self-anchored suspension bridge

图7 主缆断面布置及索股编号Fig.7 Cross-section arrangement and cable numberingof the main cable

4.2 验证流程

针对工程算例中的详细计算参数，按上述修正过程对该精细化计算方法进行验证，计算流程描述如图8。

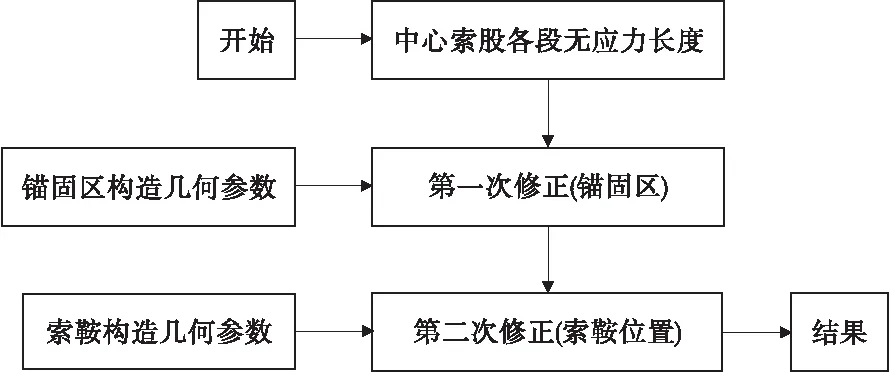
图8 主缆下料长度精细化计算流程Fig.8 Fine calculation process of the main cable fabrication length

4.3 验证结果

按图8流程计算得到主缆中心索股无应力长度为240.585 1 m，中心索股锚固段索长9.948 1 m，塔顶索鞍段11.898 3 m，通过对主缆锚固端及索鞍位置修正计算，得主缆37根索股下料长度，表1列出了主缆部分索股分别在修正位置处索长及索总长。

表1 主缆下料长度精细化修正验算结果

分析该工程实例验算结果，发现位于锚固端及主索鞍位置主缆由于各索股空间分布位置差异，主缆每股的无应力长度也不一致，部分索股与中心索股长度差值较大。经锚固端修正计算后与中心索股差值最大约5 cm，经主索鞍位置修正计算后与中心索股差值最大可达22 cm，通过该精细化修正过程计算后主缆最长索股与中心索股差值为52.9 cm，因此主缆下料长度应考虑主缆结构的空间分布位置进行精细化修正计算得到。

5 结 论

1)采用空间坐标变换法确定展索点与锚固点之间主缆各索股的有应力长度，并按照材料力学方法计算该段每股主缆的无应力长度。

2)仅介绍了主索鞍以单圆曲线形式通过塔顶时，索鞍位置主缆无应力长度的修正计算方法，其他可能存在的复合圆曲线形式索鞍，修正计算时只需分段考虑，计算方法一致。

3)主缆下料长度是控制成桥线形影响结构成桥精度的关键参数，研究了自锚式悬索桥主缆下料长度精细化计算方法，并以工程实例计算验证，发现由于主缆各索股空间分布位置差异使每根索股无应力长度差异较大，尤其是锚固区及索鞍位置影响最甚，需修正后给出各索股的精确下料长度。

[1] 潘永仁,杜国华,范立础.悬索桥恒载结构几何形状及内力的精细计算[J].中国公路学报,2000 ,13(4):33-36.

Pan Yongren,Du Guohua,Fan Lichu.A fine calculation of the geometry and internal force of suspension bridge under dead load [J].China Journal of Highway and Transport,2000,13(4): 33-36.

[2] 周孟波.悬索桥手册[M].北京:人民交通出版社,2003.

Zhou Mengbo.Suspension Bridge Handbook [M].Beijing: China Communications Press,2003.

[3] Peyrot A H,Goulois A M.Analysis of cable structure [J].Computers and Structures,1979,32(5): 805-813.

[4] 文曙东,郑凯锋,栗怀广.空间索自锚式悬索桥线形精确计算方法研究[J].公路工程,2007,32(4):127-129.

Wen Shudong,Zheng Kaifeng,Li Huaiguang.Study of an accurate calculation method for spatial cable curves of self-anchored suspension bridge [J].Highway Engineering,2007,32(4): 127-129.

[5] 唐茂林,沈锐利,强士中.悬索桥索鞍位置设计[J].公路交通科技,2001,18(4):55-62.

Tang Maolin,Shen Ruili,Qiang Shizhong.Design of suspension bridge saddle’s position [J].Journal of Highway and Transportation Research and Development,2001,18(4): 55-62.

[6] 李传习,王雷,刘光栋,等.悬索桥索鞍位置的分离计算法[J].中国公路学报,2005,18(1):63-68.

Li Chuanxi,Wang Lei,Liu Guangdong,et al.Separate calculation method on suspension bridge saddle’s position [J].China Journal of Highway and Transport,2005,18(1): 63-68.

[7] 魏建东,许惟国,刘忠玉.悬索桥鞍槽纵向曲线设计[J].西南交通大学学报,2005,40(2):215-219.

Wei Jiandong,Xu Weiguo,Liu Zhongyu.Longitudinal curve design of cable saddles in suspension bridge [J].Journal of Southwest Jiaotong University,2005,40(2): 215-219.

[8] 潘永仁,范立础.悬链线单元在悬索桥主缆下料长度计算中的应用[J].结构工程师,1998 (3):20-24.

Pan Yongren,Fan Lichu.Application of catenary element to calculating the fabrication length of the main cable of suspension bridge [J].Structural Engineers,1998 (3): 20-24.