动水压力对深水桥梁地震响应的影响

张 洁，曾金明，朱东生

(1.武昌工学院，湖北 武汉 430065；2.中交第二公路勘察设计研究院有限公司，湖北 武汉 430056；3.重庆交通大学 土木建筑学院，重庆 400074)

随着深水桥梁的建设，对处于深水中桥墩的研究也取得了很大的发展。P.Arnold，等[1]考虑水与结构的相互作用对带桩基础的海上石油平台进行了动力分析；N.W.Anthony[2]用Green函数考虑水对竖直圆柱体进行动力响应分析，并且研究了几何尺寸和材料特性两种因素对动水压力的影响；高学奎，等[3]基于Morison方程，用附加质量的形式考虑动水压力对深水桥墩的影响；赖伟[4]利用半解析半数值方法，讨论了桥墩和承台上辐射波浪动水力对深水桥梁地震响应的影响；张洁，等[5]以附加质量的形式考虑动水压力，通过对深水单墩模型、连续梁桥和连续刚构桥进行线性时程分析，研究了不同参数对动水压力的影响。现有的研究均是采用Morison方程和辐射波浪理论考虑动水压力对桥墩线性地震响应的影响，结构进入非线性后对于动水压力地震响应的研究则较少，并且采用Morison方程和辐射波浪理论两种方法计算动水压力的差异以及两种方法与规范规定动水压力值的比较都尚无具体的研究。笔者分别采用Morison方程和辐射波浪理论两种不同的方法考虑动水压力对桥墩进行线性和非线性地震响应分析，并分析比较了两种方法计算的动水压力与规范规定动水压力的差异。

1 动水压力的计算方法

1.1 Morison方程

J.R.Morison，等[6]基于忽略桥墩对水的影响提出了Morison方程。动水压力的计算公式为：

忽略动水阻力影响时墩水作用的动力平衡方程为：

由上述方程可以看出Morison方程采用附加质量的形式来考虑动水压力对深水结构的影响。

1.2 辐射波浪理论

辐射波浪理论基于边界条件求解流体速度势，然后求解动水压力，最后将求解的动水压力转化为作用在桥墩上水的附加质量来考虑地震作用下水对桥墩的影响。具体方法介绍参考文献[4，7]。

2 计算模型及动力特性分析

2.1 建立有限元模型

某一连续刚构桥，桥型布置为(90+166+90) m， 上部结构采用变截面箱梁，桥墩为矩形空心薄壁墩，1号墩和2号墩高度分别为70 m和83 m，水深分别达到56 m和66 m。采用有限元软件ANSYS对全桥建立有限元模型，主梁和桥墩采用Beam4梁单元模拟，水的附加质量采用Mass21单元模拟，计算模型如图1。

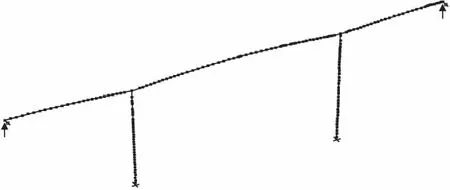
图1 桥梁计算模型Fig.1 Calculation model of the bridge

2.2 动力特性分析

分别建立不考虑水作用的计算模型、采用Morison方程考虑动水压力的计算模型(以下简称为M法)和采用辐射波浪理论考虑动水压力的计算模型(以下简称为F法)。计算3种情况下桥梁的动力特性，将桥梁的前10阶自振频率列于表1。

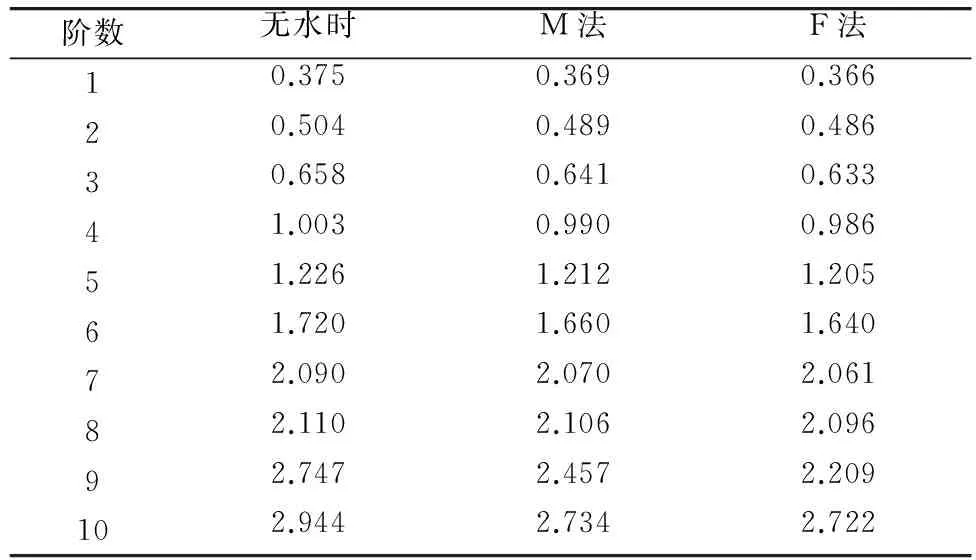
表1 桥梁的前10阶的自振频率

由表1可以得出：考虑水作用时桥梁的自振频率均小于不考虑水作用时的自振频率；采用辐射波浪理论计算的桥梁自振频率比采用Morison方程计算的桥梁自振频率要小；随着结构自振频率阶数的增加，自振频率的下降速度有增大的趋势，由此可见动水压力对结构的高阶频率影响较大。

随着阶数的增加，不考虑水作用与考虑水作用的振型略有差别，图2为不考虑水作用时桥梁结构的前5阶振型。

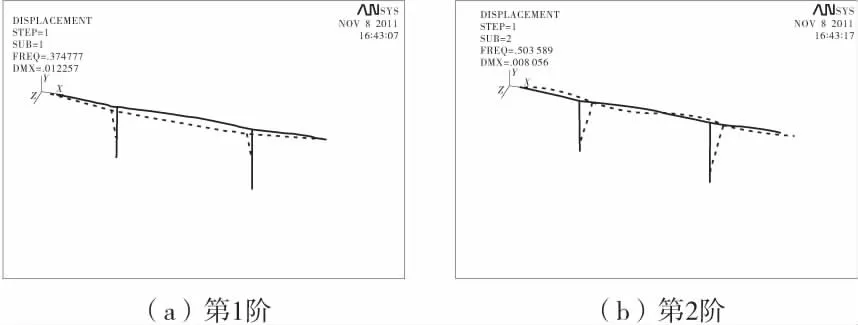
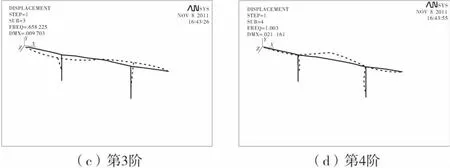
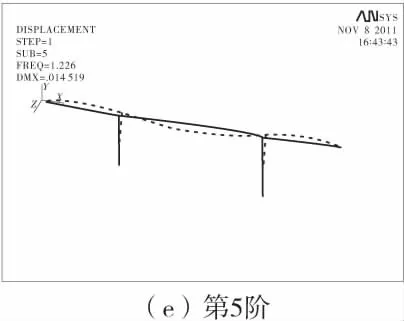
图2 桥梁结构前5阶自振振型Fig.2 Natural vibration modes of top 5 steps of bridge

3 深水桥墩的地震响应分析

根据场地特征，选择El-Centro地震波和两条人工波进行输入，分别对上述3种计算模型进行线性时程分析，3条地震波的水平加速度幅值均调整为0.2g,其加速度时程曲线如图3。

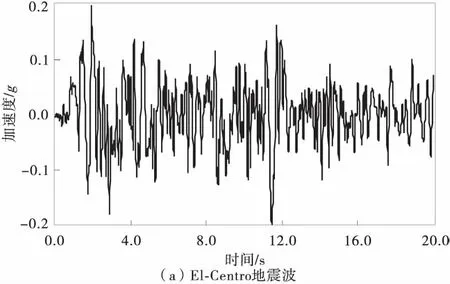
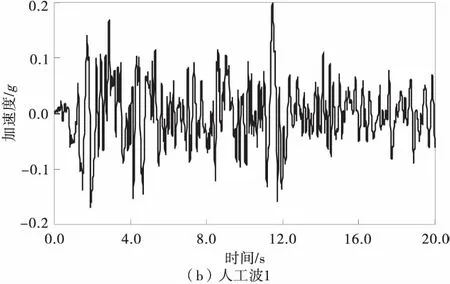
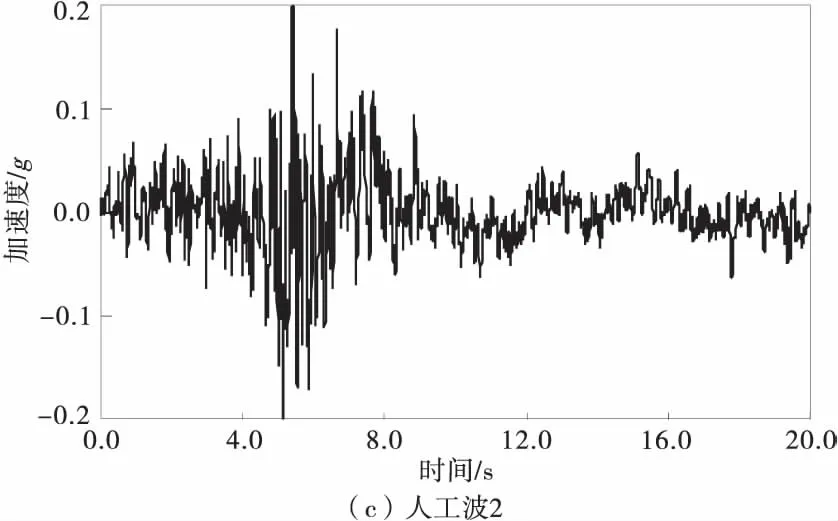
图3 地震波时程曲线Fig.3 Seismic time history curve

3.1 Morison方程考虑水作用的计算结果

采用Morison方程考虑水作用对桥墩地震响应的影响，分别计算在3条地震波作用下桥墩的地震响应。动水压力对1、2号桥墩地震响应影响类似，以1号桥墩为例，表2为3条地震波作用下桥墩地震内力响应的最大值。表3为1号桥墩在不同地震波作用下墩顶位移的最大值。

随着水深增加，动水压力对桥墩地震内力响应最大值的影响也在增大。El-Centro地震波沿顺桥向作用，水深为20 m，动水压力对墩底剪力增加量为851 kN，影响率为10%；对墩底弯矩增加量为23 034 kN·m，影响率不到5%。水深为56 m，动水压力对墩底剪力增加量为5 722 kN，影响率为30%。动水压力对墩底弯矩增加量为196 541 kN·m，影响率为20%(表2)。

横桥方向，水深为20 m，动水压力对墩底剪力的增加量为1 645 kN，影响率达到13%；对墩底弯矩的增加量为11 370 kN·m，影响率不到5%。水深为56 m，动水压力对墩底剪力的增加量为3 843 kN，影响率达到34%；对墩底弯矩的增加量为94 018 kN·m，影响率达到12%。

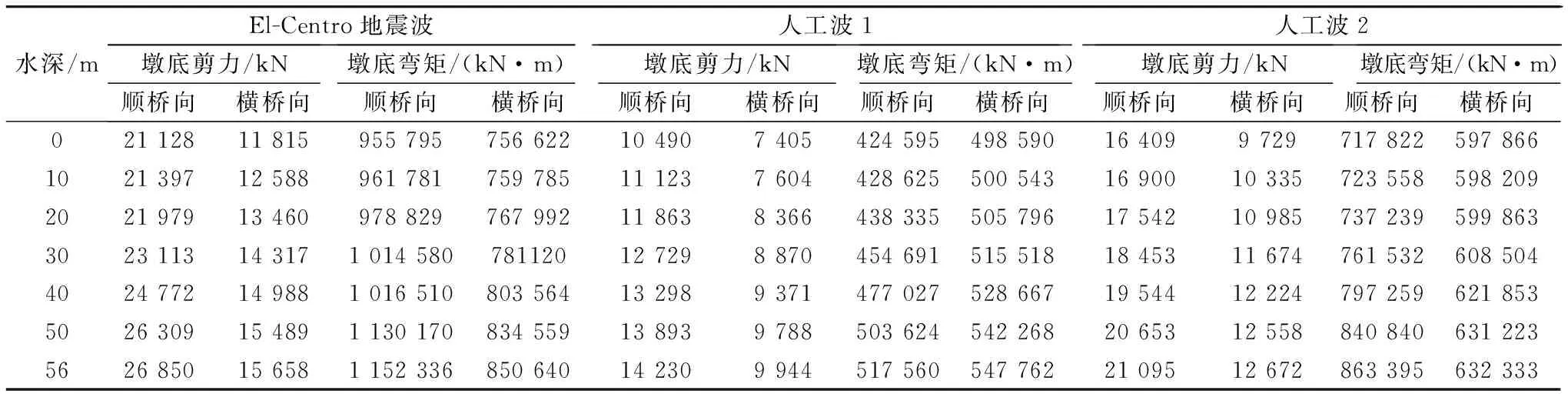
表2 桥墩地震内力响应最大值

随着水深增加，墩顶位移也在增大，即动水压力对墩顶位移影响率也在增大。水深为20 m时，动水压力对墩顶位移影响很小，影响率为2%；水深为56 m时，影响率达到20%(表3)。

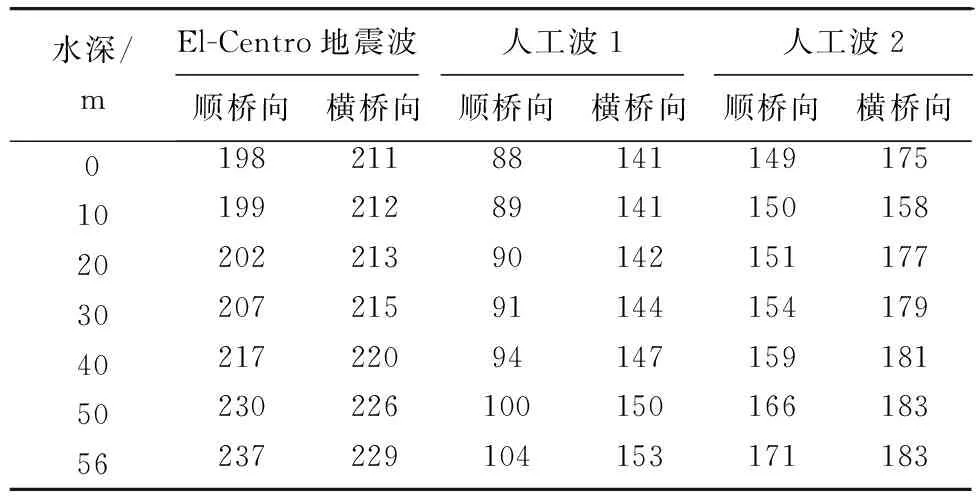
表3 桥墩墩顶位移最大响应值

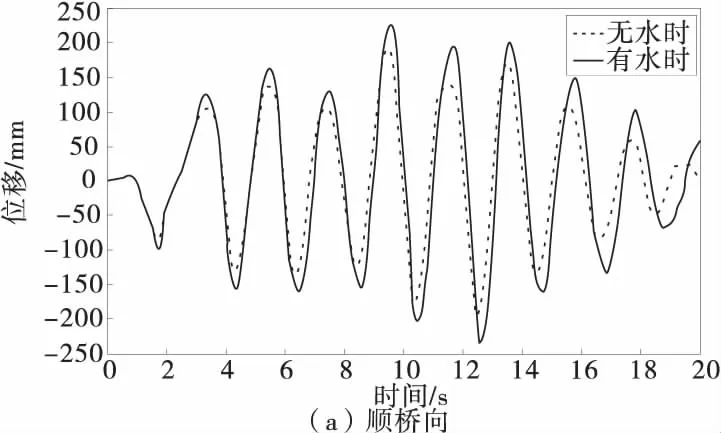
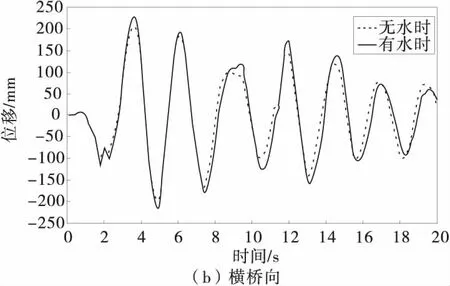
图4 桥墩墩顶位移时程曲线Fig.4 Time history curve of the displacement of pier top

图4为1号桥墩在El-Centro地震波作用下墩顶位移的时程曲线。由图4可以看出，有水(水深为56 m时)时墩顶的最大位移明显大于无水(不考虑水作用)时墩顶的最大位移。

3.2 采用辐射波浪理论考虑动水压力的计算结果

输入El-Centro地震波、人工波1和人工波2,3条地震波，采用辐射波浪理论考虑动水压力对上述3种模型进行地震响应分析。表4为不同地震波作用下1号桥墩响应的最大值。表5为1号桥墩墩顶位移的最大值。

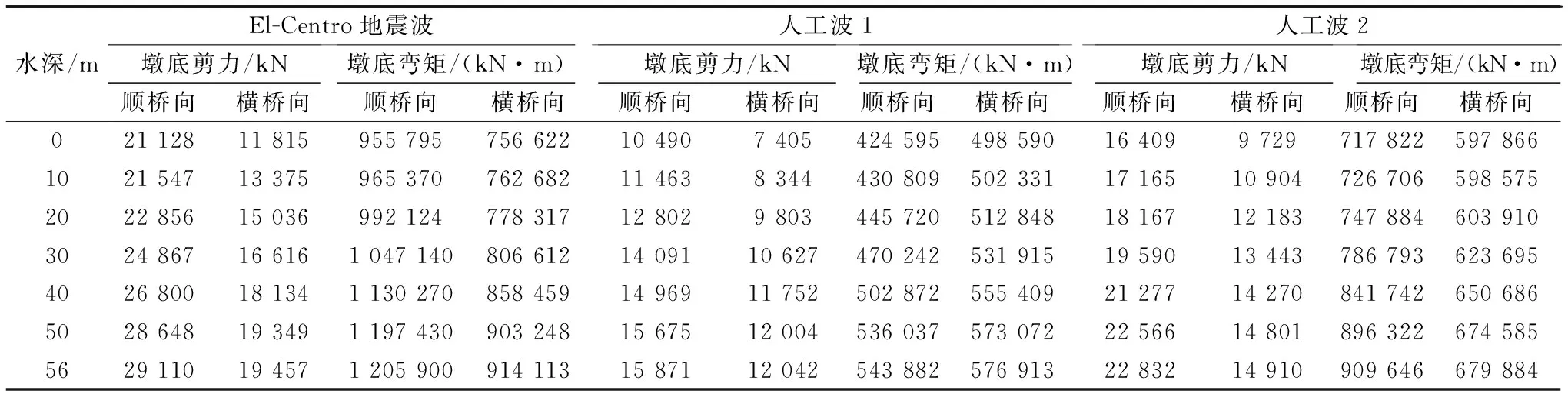
表4 桥墩地震响应的最大值

由表4可以看出，采用辐射波浪理论计算出的动水压力得到了与采用Morison方程计算动水压力相同的结论。即随着水深的增加，动水压力对桥墩地震响应的影响增大。

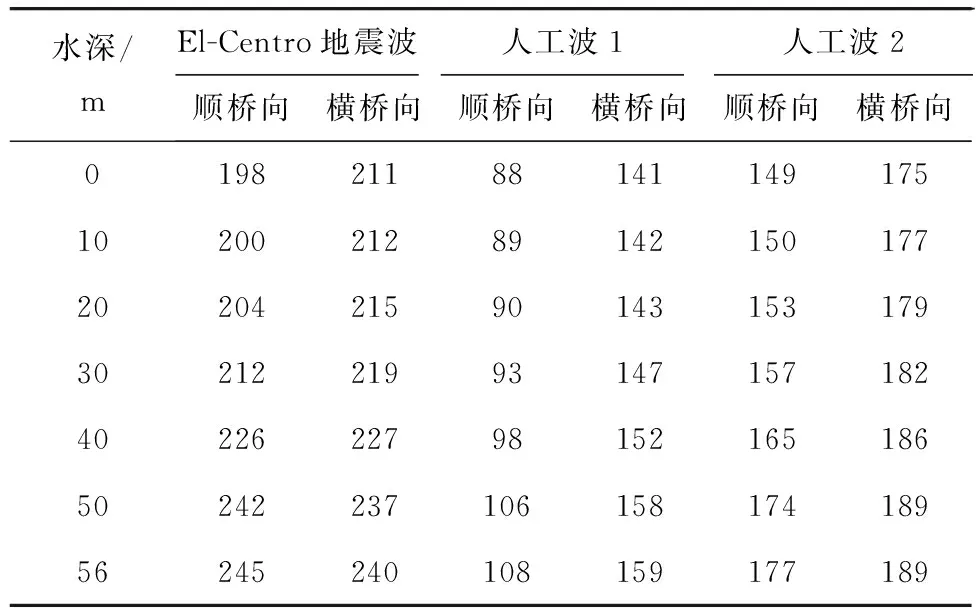
表5 桥墩墩顶位移最大值

由表5可以看出，随着水深的增加，墩顶位移明显增大，在水深为56 m时，动水压力对墩顶位移最大值的影响值达到47 mm，影响率达到24%。

3.3 两种不同计算方法的比较

分别将两种方法考虑动水压力计算的附加质量列于表6。

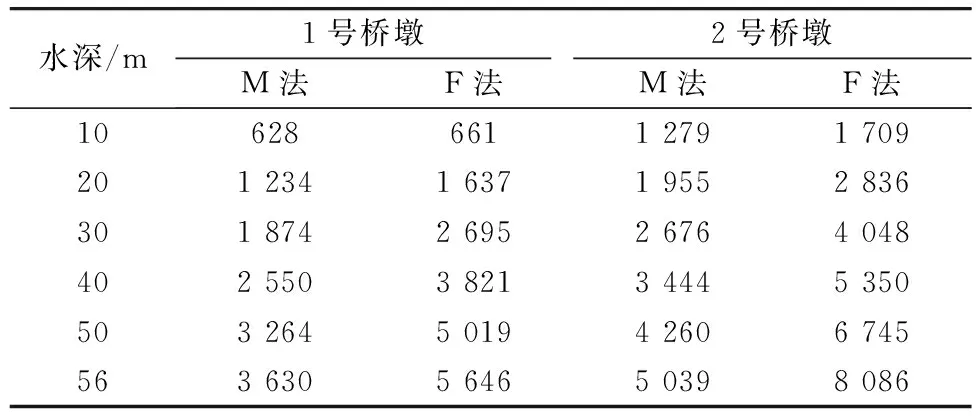
表6 不同方法计算水的附加质量

由表6得出，相同条件下，采用辐射波浪理论计算的附加质量要比采用Morison方程计算的附加质量大。

结合表2和表4的分析结果可以得出，在3条地震波作用下，采用辐射波浪理论计算的地震响应最大值都大于采用Morison方程计算的地震响应最大值。

为了更进一步说明不同水深的动水压力，以El-Centro地震波作用为例，分别把两种不同方法计算的动水压力列于表7。

由表7可以看出，随着水深的不断增加，采用两种方法计算的动水压力也在增大；采用辐射波浪理论计算的动水压力明显大于采用Morison方程计算的动水压力，并且随着水深的增加，两种方法计算动水压力的差值也逐渐增大。

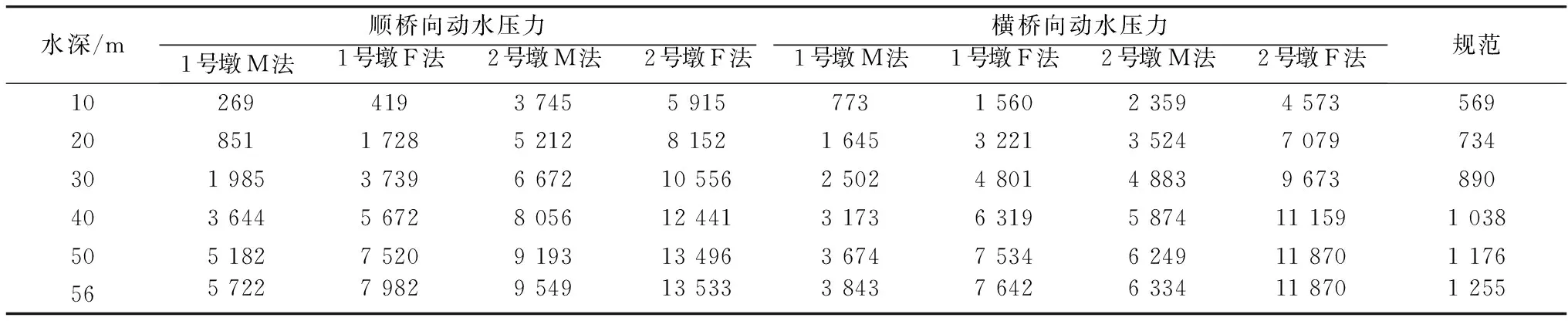
表7 地震作用下不同水深的动水压力

通过两种方法计算的动水压力与《规范》[8]规定动水压力相比较，在水深小于20 m时，规范规定的动水压力与两种方法计算的动水压力相差不大，随着水深的增加，规范规定的动水压力远远小于两种方法计算的动水压力。即在水深较大时，用规范规定的动水压力是偏不安全的。

为了具体说明Morison方程和辐射波浪理论两种计算方法的差异，分析比较两种不同方法考虑动水压力对桥墩墩底响应的影响率。

以1号桥墩为例，图5为Morison方程和只考虑外域水辐射波浪理论计算动水压力对桥墩墩底响应最大值的影响率，图6为Morison方程和辐射波浪理论计算动水压力对桥墩墩底响应最大值的影响率。

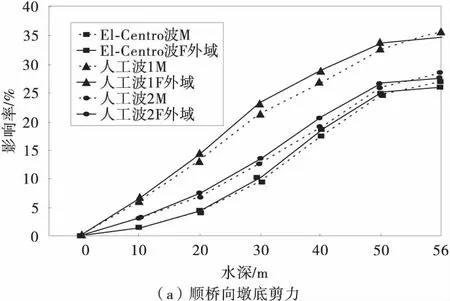
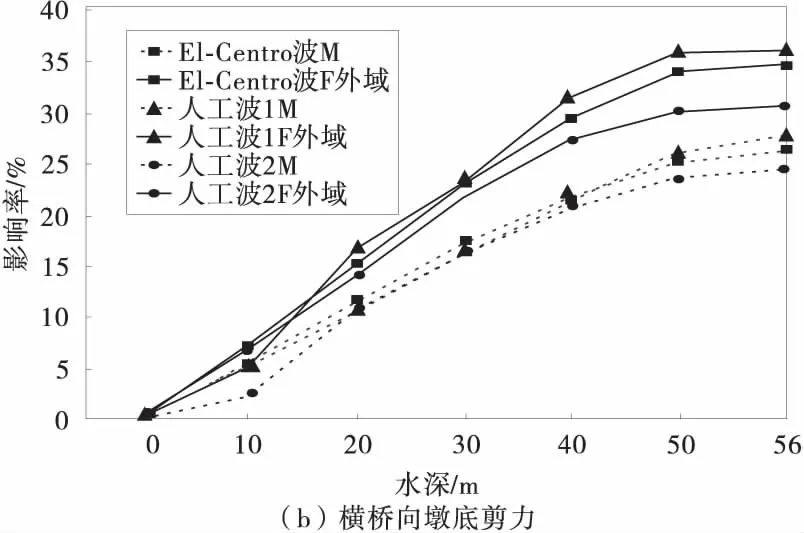
图5 动水压力对桥墩墩底响应值的影响率(外域水辐射波浪理论)Fig.5 Influence rate of hydrodynamic pressure on pierbottom(outland water radiation wave theoy)

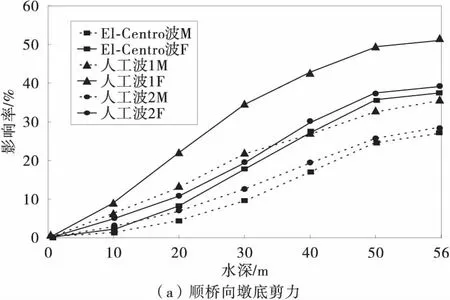
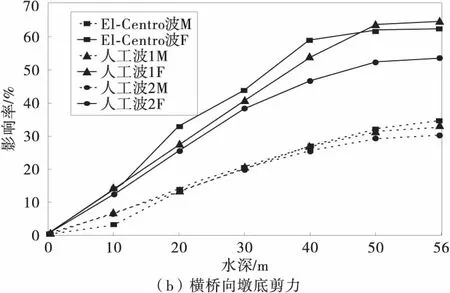
图6 动水压力对桥墩墩底响应值的影响率(辐射波浪理论)Fig.6 Influence rate of hydrodynamic pressure on pier

由图5和图6可以看出，水深小于20 m时，曲线上升的比较缓慢，随着水深的增加，曲线基本上呈直线上升。也就是说随着水深的增加，动水压力对桥墩地震响应的影响也逐渐明显。

由图5可以得出，在顺桥方向，采用Morison方程和辐射波浪理论(只考虑外域水作用)两种方法计算动水压力对墩底剪力和墩底弯矩的影响基本相同，但是在横桥方向，只考虑外域水作用时辐射波浪理论的计算结果都大于采用Morison方程计算的结果。由图6可以得出，采用辐射波浪理论计算动水压力对墩底剪力和墩底弯矩的影响都大于采用Morison方程计算动水压力对墩底剪力和墩底弯矩的影响。因此，处于深水中的空心截面桥墩，在地震的作用下，内域水的动水压力不容忽视。

4 非线性时程分析

为了分析动水压力对桥墩非线性地震响应的响应，笔者以桥墩采用纤维单元，主梁采用普通梁单元建立计算模型。钢筋采用理想弹塑性模型，混凝土采用Mander模型[9]。同样采用Morison方程和辐射波浪理论两种计算方法计算动水压力。桥墩纤维的划分如图7。

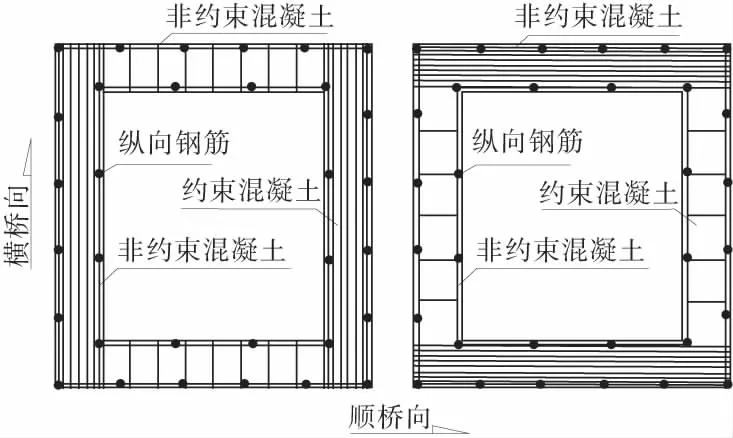
图7 桥墩截面纤维划分示意Fig.7 Sketch of pier cross-section meshing

选择El-Centro地震波，为了分析桥墩的非线性地震响应，将加速度峰值调为0.51 g。

输入El-Centro地震波，分别对上述3种计算模型进行非线性的时程分析，表8为1号桥墩非线性地震响应最大值。其中M法和F法分别表示采用Morison方程和辐射波浪理论计算水深为56 m时桥墩地震响应的最大值。

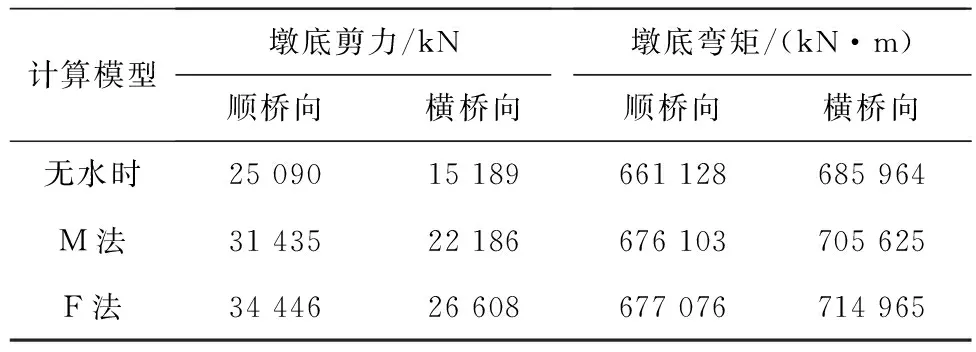
表8 桥墩非线性地震响应最大值

由表8可以看出，在顺桥方向，采用Morison方程考虑动水压力计算的桥墩墩底剪力、弯矩分别比无水时增加了25.3%，2.3%，而采用辐射波浪理论计算的墩底剪力、弯矩分别比无水时增加了37.3%，2.4%。在横桥方向，采用Morison方程考虑动水压力计算的桥墩墩底剪力、墩底弯矩较无水时分别增加了46.1%、2.9%，而采用辐射波浪理论计算的墩底剪力、墩底弯矩较无水时分别增加了75.5%，4.2%。

比较动水压力对桥梁线性及非线性地震响应的影响，当桥墩进入非线性后动水压力对桥墩墩底弯矩响应的影响减小，但是对剪力的影响度却有近两倍的增加。因此，当深水桥梁在强震作用下进入非线性后，采用线性的计算结果不能真实的反应出桥梁的地震响应，应该采用非线性的分析方法。

为了更进一步分析动水压力对桥墩非线性地震响应的影响，图8为1号墩在El-Centro地震作用下墩底的滞回曲线。

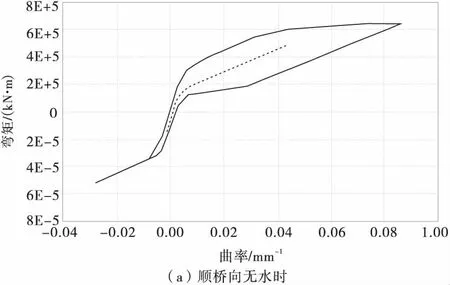
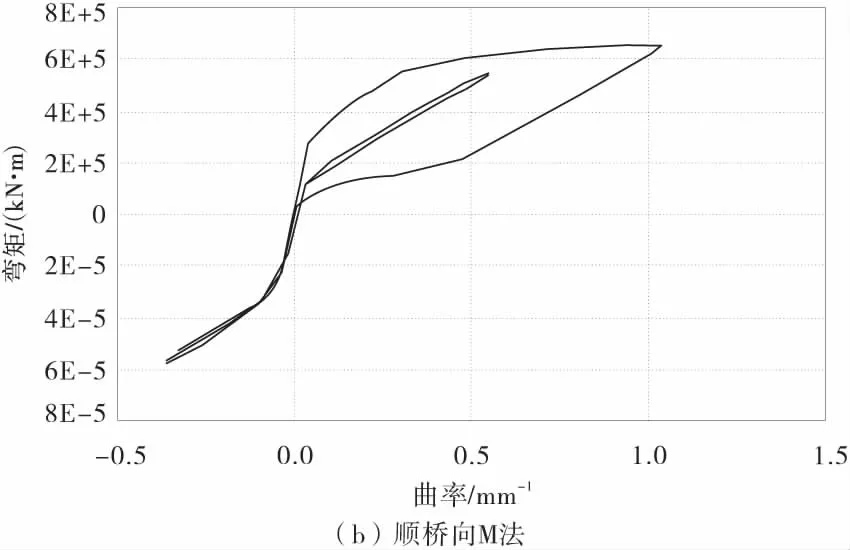
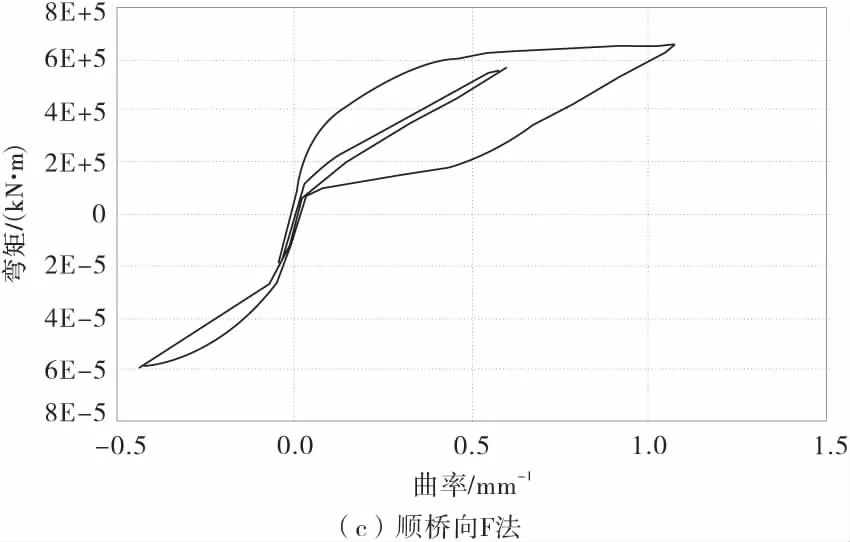
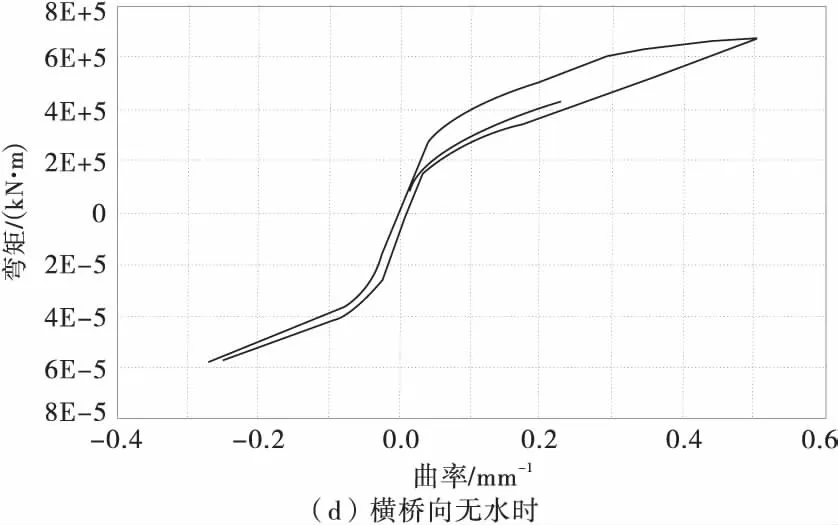
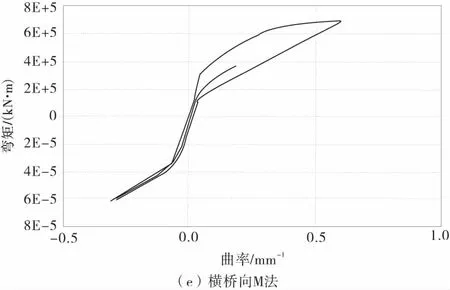
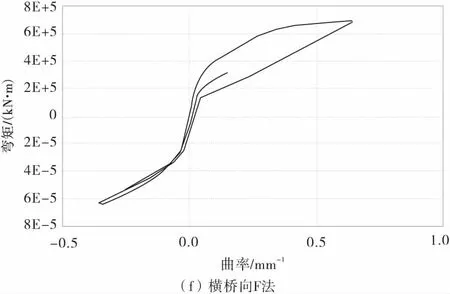
图8 墩底弯矩-曲率滞回曲线Fig.8 Moment-curvature hysteresis loop at the bottom of piers

由图8可以发现，在E2地震作用下，1号桥墩已经进入了屈服阶段。在顺桥向地震作用下，桥墩墩底在无水时、M法、F法计算得到的曲率延性系数分别为2.40，3.11和3.24。其中定义曲率延性系数为墩底最大曲率与屈服曲率之比。而在横桥向，桥墩墩底在无水时、M法、F法计算得到的曲率延性系数分别为1.70，2.00和2.13。由此可以看出考虑动水压力后桥墩墩底的曲率延性系数提高了，桥墩墩底的非线性程度更高。

由计算结果发现，E2地震沿着顺桥方向作用下，1号桥墩墩底在无水时、M法、F法计算的屈服时刻分别为3.20，2.14，1.70 s；在横桥方向，1号桥墩墩底在无水时、M法、F法计算的屈服时刻分别为3.54，2.40，2.12 s，即考虑水作用时1号桥墩墩底进入屈服的时刻有所提前。这是因为采用Morison方程和辐射波浪理论考虑动水压力增大了桥墩的质量，延长了桥墩的自振周期，并且采用辐射波浪理论计算的附加质量最大，1号桥墩墩底进入屈服的时刻也最早。

5 结 论

通过建立不考虑水作用、采用Morison方程考虑水作用和辐射波浪理论考虑水作用3种计算模型，分别对3个计算模型进行动力特性分析、线性时程分析和非线性时程分析；得出以下主要结论。

1)考虑水作用时桥墩自振频率比不考虑水作用时桥墩自振频率小；采用辐射波浪理论考虑动水压力计算桥梁的自振频率小于采用Morison方程计算的桥梁自振频率。

2)分别采用Morison方程和辐射波浪理论对深水桥墩进行线性时程分析，得出动水压力增大了桥墩的地震响应，并且两种不同计算方法考虑动水压力对桥墩地震响应的影响不同。

3)分析比较两种方法与规范规定计算的动水压力，当水深较大时，用规范规定计算深水桥墩的动水压力偏不安全。

4)当桥墩进入非线性后动水压力对桥墩墩底剪力、墩底弯矩和墩底屈服时刻的影响发生较大变化，因此当深水桥梁在强震作用下进入非线性后，采用线性的计算结果不能真实的反应出桥梁的地震响应，应该采用非线性的分析方法。

[1] Arnold P,Bea R G,Idriss L M.A Study of Soil-Pile-Structure Systems in Severe Earthquakes[C]//The 9thAnnual Offshore Technology Conference,Houston: Offshore Technology Conference,1977: 27-49.

[2] Anthony N W.Earthquake response of submerged circular cylinder [J].Ocean Engineering,1986,13(6): 569-585.

[3] 高学奎,朱晞.地震动水压力对深水桥墩的影响[J].北京交通大学学报:自然科学版,2006,30(1):55-58.

Gao Xuekui,Zhu Xi.Hydrodynamic effect on seismic response of bridge pier in deep water [J].Journal of Beijing Jiaotong University: Natural Science,2006,30(1): 55-58.

[4] 赖伟.地震和波浪作用下深水桥梁的动力响应研究[D].上海:同济大学,2004.

Lai Wei.Dynamic Responses of Bridges in Deep Water under Combined Earthquake and Wave Actions [D].Shanghai: Tongji University,2004.

[5] 张洁,朱东生,张永水,等.考虑动水压力作用的深水桥墩地震响应分析[J].重庆交通大学学报:自然科学版,2012,31(3):357-361.

Zhang Jie,Zhu Dongsheng,Zhang Yongshui,et al.Seismic response analysis of piers in deep water considering hydrodynamic pressure interaction [J].Journal of Chongqing Jiaotong University: Natural Science,2012,31(3): 357-361.

[6] Morison J R,O’Brien M P,Johnson J W,et al.The force exerted by surface wave on piles [J].Journal of Petroleum Transactions,1950,2(5): 149-154.

[7] 刘振宇,李乔,赵灿晖,等.深水矩形空心桥墩在地震作用下附加动水压力分析[J].振动与冲击,2008,27(2):53-56.

Liu Zhengyu,Li Qiao,Zhao Canhui,et al.Additional hydrodynamic pressure on rectangular hollow piers in deep water due to earthquake [J].Journal of Vibration and Shock,2008,27(2): 53-56

[8] JTG/T B02-01—2008 公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.

JTG/T B02-01—2008 Seismic Design of Highway Bridges[S].Beijing: China Communications Press,2008.

[9] Mander J B,Priestley M J N,Park R.Theoretical stress-strain model for confined concrete [J].Journal of Structural Engineering,1988,114(8): 1804-1826.