燃气涡轮机高速转子临界转速仿真

李日朝, 郝东旭



燃气涡轮机高速转子临界转速仿真

李日朝1, 郝东旭2

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 2. 中国人民解放军 92840部队, 山东 青岛, 266405)

工程应用中燃气涡轮机高速转子需要确定其临界转速, 以确保发动机在安全的转速范围内工作, 而不发生共振。以一种高速转子系统为研究对象, 分别采用传递矩阵法和有限元法对其临界转速进行求解, 通过试验测试, 验证了这两种方法的可行性和精确性, 为工程设计提供了依据。

燃气涡轮机; 临界转速; 传递矩阵; 有限元法

0 引言

为了提高涡轮机的经济性, 在一定的圆周速度限制下, 需将涡轮盘的转速不断提高, 在工程中, 高速回转机械需要计算其临界转速, 以确保涡轮机的工作转速在安全范围内, 不发生共振。常用的对转子系统临界转速计算有传递矩阵法和有限元法, 传递矩阵法具有占用储存空间小, 计算速度快, 能计算至任意高阶固有频率, 无需预知振型等优点。但对于结构复杂的涡轮盘转子, 解析法的计算过程十分繁琐, 而且由于各种因素会使计算结果受到影响, 从而降低计算精度。而有限元在处理转子动力学问题时, 可以很好地兼顾模型的完整性和计算的效率[1-3]。本文对一种高速转子系统的临界转速采用解析法和有限元法进行求解, 把2种方法所求的数值与试验测试结果进行对比分析, 考查计算结果的准确性和可行性。

1 转子模型描述

燃气涡轮机高速转子由涡轮盘、轴、花键套、输出齿轮轴和4个深沟球轴承等部分组成, 安装方式为外伸式。燃气涡轮转子系统剖面图见图1。

图1 涡轮转子结构简图

将图1简化成图2的模型, 按照传递矩阵法要求的原则分成13段有质量的均质轴(0-1、1-2、2-3、3-4、4-5、5-6、6-7、7-8、8-9、9-10、10-11、11-12、12-13)、1个涡轮盘(1)、4个弹性支撑(3, 4, 8, 12)。相关参数见表1~表3。

图2 涡轮转子系统简化图

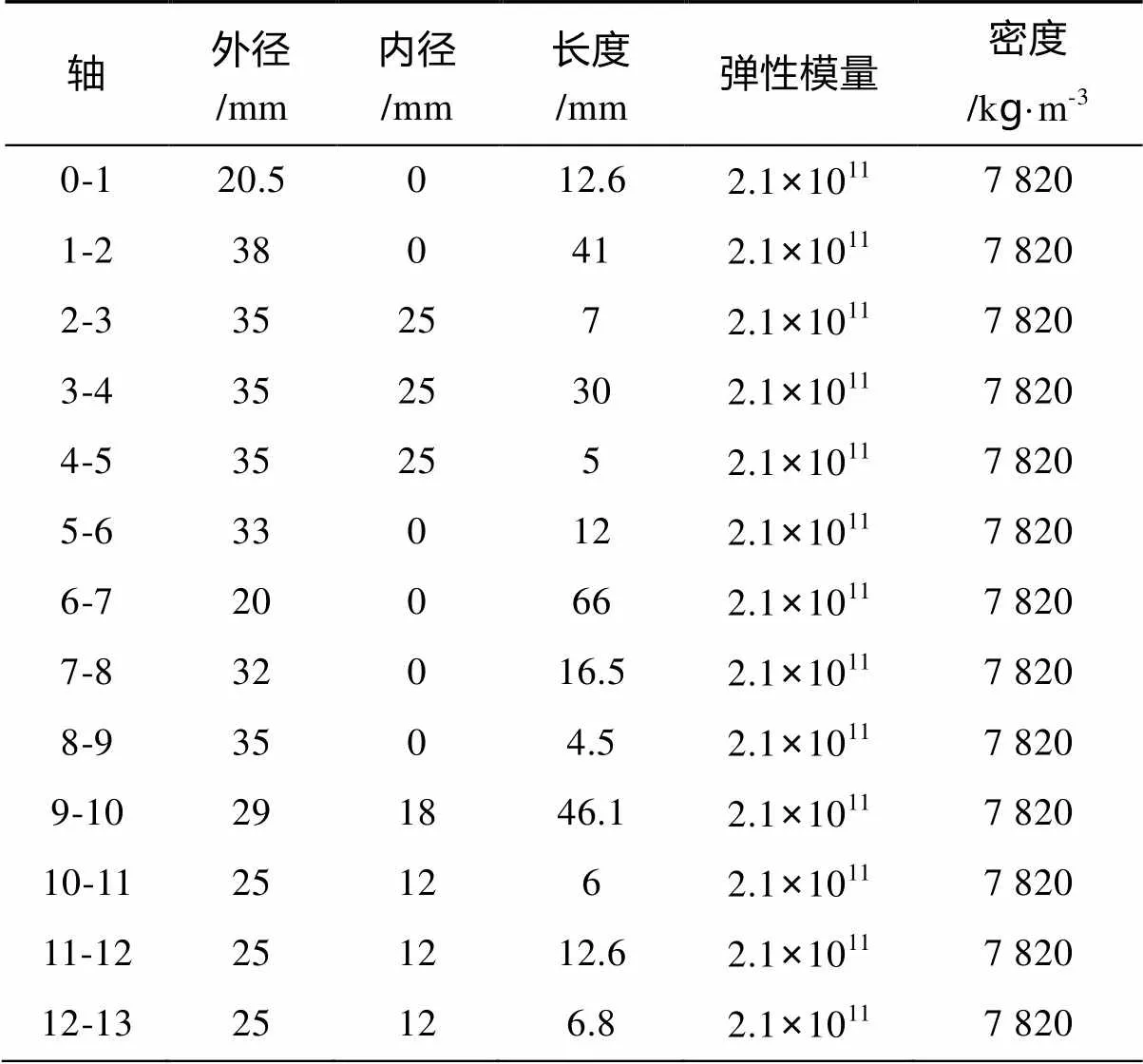
表1 涡轮转子系统均质轴参数

表2 涡轮转子系统涡轮盘参数

表3 涡轮转子系统弹性支撑参数

2 临界转速计算方法

2.1 传递矩阵法

2.1.1 轴单元传递矩阵

均质轴在不计轴向力、不计转动惯量时两端截面上状态参数之间的关系为[1]

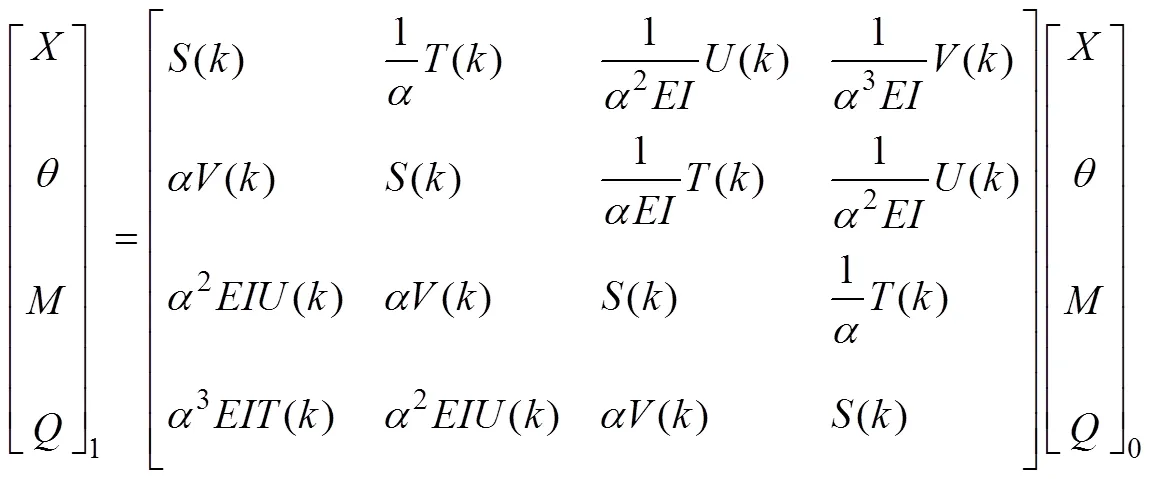
式中:为单位长度轴段的质量;为轴段材料的弹性模量。

均质轴传递矩阵为

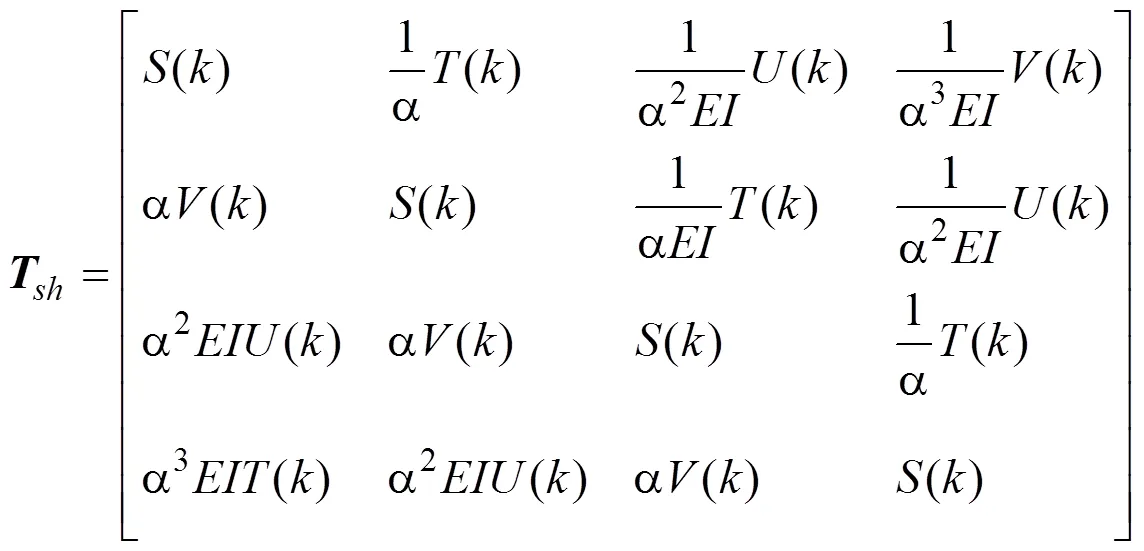
2.1.2 涡轮盘传递矩阵

轮盘的传递矩阵[1]为

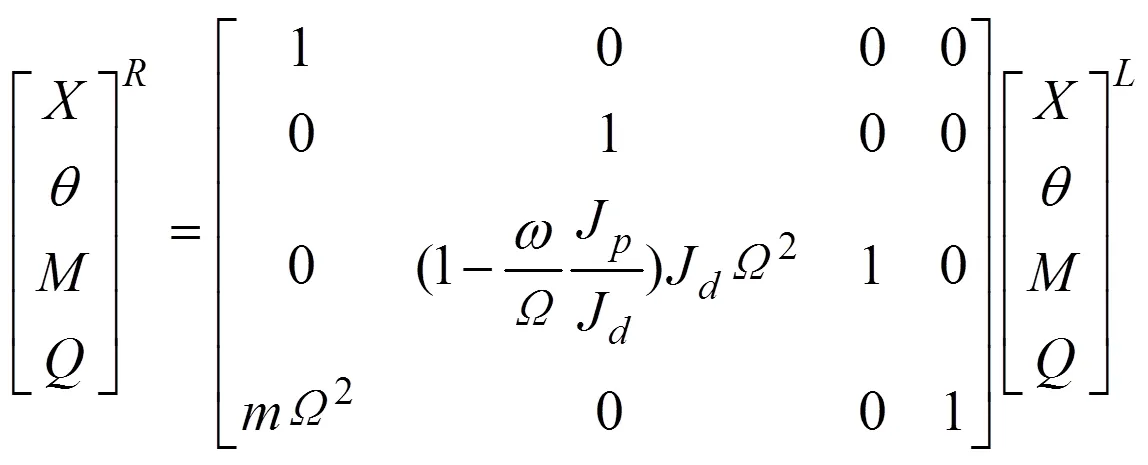
式中:为涡轮盘质量;J为涡轮盘极转动惯量;J为涡轮盘直径转动惯量;为涡轮盘转动角速度;为系统固有频率。

2.1.3 弹性支撑传递矩阵

弹性支撑左右两端的参数关系[1]为

2.1.4 边界条件

本系统两端均为自由悬臂,其截面状态参数如下。起始端状态矩阵

终端状态矩阵

根据以上计算参数, 利用传递矩阵法计算系统临界转速, 计算结果如图3所示。

图3 临界转速曲线

曲线与纵坐标0的交点所对应的转速即为系统临界转速点。由图3可知, 系统1阶临界转速为4469rad/s。临界转速同转子的弹性和质量分布等因素有关。对于具有有限个集中质量的离散转子系统, 临界转速的数目是有限的; 对于质量连续分布的弹性转子系统, 临界转速有无穷多个。工程上有实际意义的主要是前几阶, 过高的临界转速已超出了转子可达的工作转速范围。

2.2 有限元方法

计算旋转结构的临界转速就是计算它的固有频率, 固有频率分析在ANSYS中被称为模态分析, 共有7种提取方法[4], 即子空间法、分块Lan- czos法、PowerDynamics法、缩减法、非对称法、阻尼法和QR阻尼法。其中只有阻尼法和QR阻尼法允许在结构中考虑阻尼。本文采用QR阻尼法。

涡轮转子系统的3D实体模型如图4所示。

图4 涡轮转子系统3D实体图

考虑到转子动力学分析的特点, 选用3D实体单元SOLID92建模, 对模型中轴承的弹性支撑分别用4个2D弹簧单元COMBIN14仿真。SOLID92是3D结构单元, 有10个节点, 每个节点有,,共3个自由度, 并具有塑性、超弹性、压力硬化、大变形和大应变等特点, 很适合转子3D造型。此处取网格大小为0.005, 划分方式为智能。COMBIN14由2个节点组成, 每个节点有2个自由度, 不考虑弯曲和扭转, 假设周向刚度对称, 并忽略阻尼。按此划分好网格的计算模型如图5所示, 其中节点数为155258, 单元数为40 727。

图5 涡轮转子系统网格划分

采用有限元方法计算转子临界转速时, 转子会出现正进动和反进动。由于陀螺效应的作用, 随着转子自转角速度的提高, 反进动固有频率降低, 而正进动固有频率将提高。根据临界转速的定义, 应只对正进动固有频率进行分析。在后处理中首先剔除负固有频率, 然后分析各阶模态模型确定同一阶振型的正进动与反进动固有频率。改变转子自转角速度, 计算出新的, 最后画出曲线, 即转子坎贝尔曲线, 如图6所示。

图6 涡轮转子系统坎贝尔曲线

根据临界转速定义, 当=时, 即等速线与坎贝尔曲线处的即所求临界转速对应的频率。根据图6可知, 该转子的1阶临界转速665× 6.28=4176.2 rad/s。

3 试验测试验证

3.1 试验设备及测试方法

转子系统动力特性试验台如图7所示, 电机输出端通过膜片联轴器连接齿轮箱的输入端, 齿轮箱内部增速齿轮对使齿轮箱输出端具有较高转速, 齿轮箱输出端通过花键联轴器连接试验件。

图7 试验台实物图

本试验采用电涡流位移传感器和压电式加速度传感器来测量系统的振动。将传感器测试到的信号输送到USB4716数据采集卡, USB4716数据采集卡通过USB接口连接到PC机上, 在PC机上通过LABVIEW程序的界面实时监测和实时保存采集到的信号。LABVIEW软件内置滤波器模块, 可以滤掉噪声和谐波, 此外该软件可以进行快速傅里叶变换运算, 在控制面板上实时观测到幅频图, 并可通过加速度以及振幅的变化求出当前转速。LABVIEW程序的实时监测界面如图8所示, 可通过界面观测到轴心轨迹、加速度、振幅等信号, 同时可以实时保存所采集到的数据。

图8 Labview实时监控界面

3.2 试验结果与对比

对采集的数据进行分析计算, 取每个转速下采集的所有振幅的均方根值作为该转速下的幅值, 得到涡轮盘水平方向的幅频图如图9。可以看出, 涡轮盘在转速40872 r/min时, 振幅达到最大, 因此判断该转速为转子系统的1阶临界转速。

3种方法所得转速结果。传递矩阵法: 42697 r/min; 有限元法: 39898 r/min; 试验测量: 40872 r/ min。前2种方法与试验测量的结果比较。传递矩阵法: (42697－40872)/40872×100% = 4.46% , 相差4.46%; 有限元法:(40872－39898)/40872×100%=2.38% , 相差2.38 %。

图9 水平方向的幅频图

4 结束语

对于燃气涡轮机的设计, 转子动力学设计是一个重要环节, 首先就要对其进行动力学分析, 确保转子系统的工作转速离临近的临界转速有足够的裕度, 以免在正常工作时产生共振, 这就要求尽可能在设计阶段正确地预计转子-支撑系统的临界转速。本文通过传递矩阵法及有限元法分别计算了涡轮转子系统临界转速, 并通过试验验证了计算的准确性。

[1] 刘延柱. 振动力学[M]. 北京: 高等教育出版社, 1998.

[2] 张小龙, 何洪庆. 涡轮泵转子的临界转速研究(V)临界转速的有限元法[J]. 推进技术, 2000, 6(3):40-42.Zhang Xiao-Long, He Hong-qing. Critical Rotation Speed of Turopump rotors(V) Finite Element Methord for Criti- cal Rotation Speed Calcuation[J]. Journal of Propulsion Technology, 2000, 6(3):40-42.

[3] 秦然, 张建伟. 转子临界转速的求解方法比较[J]. 沈阳化工学院学报, 2007, 21(1): 74-76, 80.Qin Ran, Zhang Jian-wei. Comparison of Rotor Critical Rotation Speeds Solution Method[J]. Journal of Shenyang University of Chemical Technology, 2007, 21(1): 74-76, 80.

[4] SaeedMoaveni. 有限元分析: ANSYS理论与应用[M]. 欧阳宇, 王崧, 等译. 北京: 电子工业出版社, 2003.

[5] Nicola Diolaiti. Robotic Interaction Analysis and Control [D]. Bologna: University of Bologna, 2005.

[6] Wang L Q, Li W Z, Gu L, et al. Reducing Vibration with Friction-Damping in High-Speed Rotor System[J]. Tran- sactions of Nanjing University of Aeronautics & Astronautics, 2007, 24(1): 48-53.

[7] 周松江, 赵行明. 弹性环-挤压油膜系统双稳态和临界转速[C]//中国航空学会百年学术论坛动力分论坛文集-第五届动力年会结构强度振动分册,北京,2003:99-106.

(责任编辑: 陈 曦)

Simulation on Critical Rotation Speed of High-Speed Rotor of Gas Turbine

LI Ri-zhao, HAO Dong-xu

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. 92840thUnit, The People′s Liberation Army of China, Qingdao 266405, China)

To ensure a gas turbine working in the safe rang of speed without resonance, it is necessary to obtain the critical rotation speed of its high-speed rotor. In this study, the critical rotation speed of a high-speed rotor is calculated by using the transfer matrix method and the finite element method, respectively. Experiments verified the feasibility and accuracy of the two methods. This study may provide a support to engineering design of high-speed rotor of gas turbine.

gas turbine; critical rotataion speed; transfer matrix; finite element method

TJ630.32

A

1673-1948(2014)06-0457-04

2014-09-05;

2014-10-17.

李日朝(1970-), 男, 硕士, 高工, 研究方向鱼雷热动力技术.