单液滴撞击水平冷板面的模拟研究

王 瑾，李占勇，徐 庆，王瑞芳

(天津科技大学机械工程学院，天津 300222)

单液滴撞击水平冷板面的模拟研究

王 瑾，李占勇，徐 庆，王瑞芳

(天津科技大学机械工程学院，天津 300222)

针对喷雾冷冻干燥中液滴在设备壁面的冷冻沉积问题，在前期单液滴撞击水平放置冷板面的实验基础上，建立了单液滴与冷板面撞击的模型，利用水平集方法与固化模型相结合，模拟了蒸馏水液滴(直径为3.2mm，温度为293K)分别从100、250、500mm高度撞击不锈钢板面(温度为268K和253K)的过程．模拟的最大铺展直径同实验对比，误差小于10%，证明该模型可适用于低黏度、低密度的单液滴撞击水平冷板面的情况．

单液滴；冷板面；模拟；水平集方法；固化模型

喷雾冷冻干燥是一种新型的工程技术，主要用于奶粉、药物蛋白、卵清蛋白、流感疫苗[1–4]等高附加值热敏性产品的制备，产品形态也多种多样，合理地优化其过程工艺有助于制备比表面积大、空隙率高、结构均匀稳定的粉体[5]．雾化液滴在设备壁面的冷冻沉积是在喷雾冷冻干燥技术应用中的常见问题．此问题可以通过实验方法解决，如Xu等[6–7]对单液滴撞击不同材质的冷板面进行实验，得出不同温度和不同撞击速度下单液滴的铺展直径和铺展因子，提出了减少冷冻沉积发生的方法；还可以通过模拟设备流场的方法解决冷冻沉积问题，如Anandharamakrishnan等[8]利用3,D计算流体动力学模型模拟喷雾冷冻干燥设备的内流场，以减小雾化液滴与设备壁面的接触几率；也可直接对单液滴撞击冷板面进行模拟研究，反映液滴在板面的铺展冻结过程，可以弥补实验法无法直接测得的数据，如耿县如等[9]以单个雾化液滴为研究对象，模拟了液滴大小、气体流速和环境温度等参数对液滴冻结过程的影响，发现液滴越大冻结时所需的形核时间和完全固化时间越长，而且冻结过程随着气体流速的增大和环境温度的降低而缩短，为分析液滴撞击板面后的冻结过程提供了理论依据．

液滴撞击冷板面的模拟可以认为是存在相变的自由表面流动问题，涉及移动界面．同时，考虑凝固相变时，对流体有效的控制方程对固体不再适用，自由表面的流动也会变得更加复杂，需要追踪相界面的变化．

目前对于处理液体凝固的计算方法有2种，其中1种是对自由表面及流体中的焓值变化量进行追踪．Pasandideh-Fard等[10]采用改进的VOF法模拟了锡液滴撞击温度为25～240℃的不锈钢板面的凝固过程，并且模型中引入了液滴接触角及液滴底部界面的传热系数，该系数由实验测得并作为模拟的边界条件．但是VOF方法由于数值不连续，所以在计算界面的位置和平均曲率(确定表面张力)时精度较低.第2种方法是将流体描述为多孔介质[11–13]．

Voller等[14]使用固定网格来模拟对流扩散条件下的液体凝固情况，将焓值的变化转化为关于温度的函数，且定义全液相时孔隙率为1、全固相时孔隙率为0，将流体速度与孔隙率相乘，当流体速度为0时，则可以认为流体固化完全，通过在Navier-Stokes方程中修正体积力源项来模拟相变过程．而Marin[15]利用此方法模拟了直径2mm的铝液滴撞击板面的固化过程，结果表明此方法对模拟高黏度、高密度且具有高熔化潜热的材料撞击板面的问题具有很好的适用性．

本文结合Sussman等[16]描述的水平集方法与Marin[15]使用的固化模型，使用基于温度的热传导方程代替原有的焓值方程，并且在热容源项中加入熔化潜热，以解决低黏度、低密度液滴(如蒸馏水等)撞击板面的相变问题．

1 控制方程与计算方法

1.1 流体流动控制方程

液滴与空气的速度场和压力场控制方程用不可压缩Navier-Stokes方程表示：

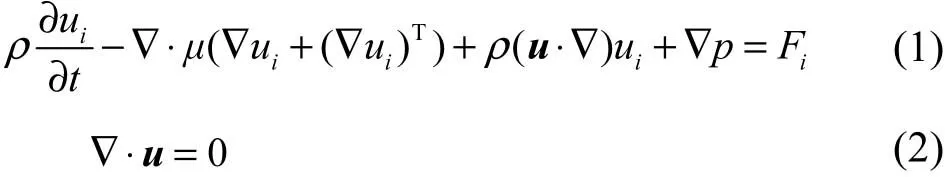
式中：∇为哈密尔顿算符；t为时间；µ为流体黏度；ρ为流体密度；u为速度矢量；ui为速度矢量在i方向上的数值，i为r或z，r表示液滴铺展直径方向，z表示液滴铺展高度方向；p为流体压强；iF为体积力在i方向上的数值．气液两相界面用固定网格的欧拉方程处理，由于气体和液体之间的密度差，所以气液接触面存在表面张力的影响．体积力包括重力和水平集法的表面张力，由于本模型中存在液滴固化的情况，因此体积力还包含依赖于凝固过程的固体比例源项，该源项将在1.3节详细说明．

1.2 水平集方法

水平集方法可以用于求解包含表面张力相的不可压缩两相流动．在水平集方法中，使用水平集函数ϕ来描述两相交界面．在连续相中水平集函数始终为正，在分散相中始终为负，两相交界的自由表面由水平集函数为零的点构成，即：连续相ϕ(x, y, t)＞0；交界面ϕ(x, y, t)＝0；分散相ϕ(x, y, t)＜0．

从自由面定义可知，交界面上的单位法向量n由分散相指向连续相，交界面的曲率κ可以用水平集函数表示为

交界面的运动可通过水平集函数的对流表示为

描述物性急剧变化的Heaviside函数可以用水平集函数表示为

Heaviside函数作用在液相与气相界面间平滑过渡，液相赋值为1、气相赋值为0．流体不同属性的改变可以用Heaviside的函数分别进行计算，公式见式(7)—式(9)．

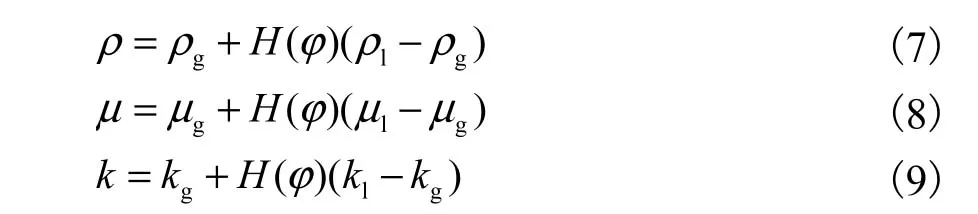
式中：k为导热系数；下标g表示气体，l表示液体．

表面张力在Navier-Stokes方程中只作用在气液交界面，由式(10)定义．

式中：σ为表面张力系数；κ为曲率；n为液–气界面的单位法向量．

采用平滑Dirac delta函数扩展出给定界面宽度的近似方程：

式中，n2为此函数的参数．

1.3 固化控制方程

纯净流体是否发生凝固由熔点决定．在流体冷却过程中，一旦温度低于熔点，在温度继续降低之前流体开始释放相变潜热．在多组分体系中，相变发生在从固体开始出现到流体最后凝固的温度范围内．在此过程中熔化潜热不断释放．

传热方程用系统温度形式表示为

首先，将相变时的固体组分FS表示为与温度相关的函数：

式中：T为温度；Tm为蒸馏水发生凝固温度；ε为冻结温度范围中间值．

为了将固化过程并入体积力中，可以将液相看作是一种多孔介质，孔隙率λ依赖于温度，全液相对应于孔隙率为1，全固相对应于孔隙率为0，孔隙率定义为

对于固化过程，固相源项S定义为

式中，A是孔隙率的函数，根据式(16)定义．

式中，C、q均为函数A的参数．

当温度位于液相线以上时，系统处于全液态，固体比例源项取值为0，对Navier-Stokes方程没有任何改动．当温度处于液相线和固相线之间，固液共存为多孔区域，A值增大并影响瞬态、对流和扩散项，流动方程近似相当于多孔介质中的Darcy定律．当温度降低到固相线以下时，孔隙率接近于0时(固相)，该源项使得速度值趋于0(固相)．式中的C和q是能达到预期的效果的任意常数，通常C要足够大且q要足够小到避免被0除．

水平集函数定义了两相初始态(该模拟中是气相与液相)的交界面，当固化发生时，固相会出现在液相中，所以需要修改固相源项S，使其严格作用在液相中．FS项在方程中都要乘以Heaviside函数H(ϕ)(在液态时H(ϕ)＝1)，这样就确保了固化模型是液相独有，无论气体温度如何，模型都不会影响气相．

式(1)中的体积力最终可以表示为

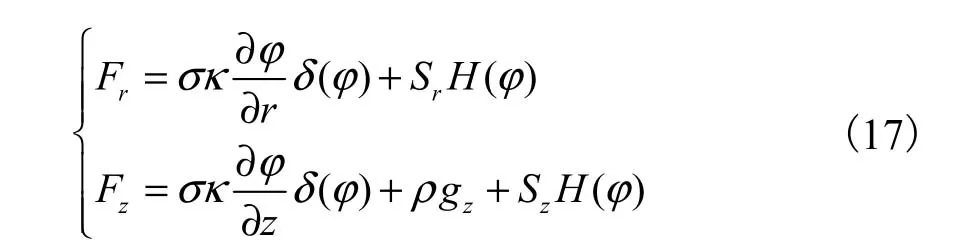
总体系热量由两部分组成：显热h和潜热ΔH．显热由式(18)计算．

式中，cp为比定压热容．

潜热的释放与温度的下降呈线性变化，发生相变的焓值作为温度的函数可以写成式(19)形式．

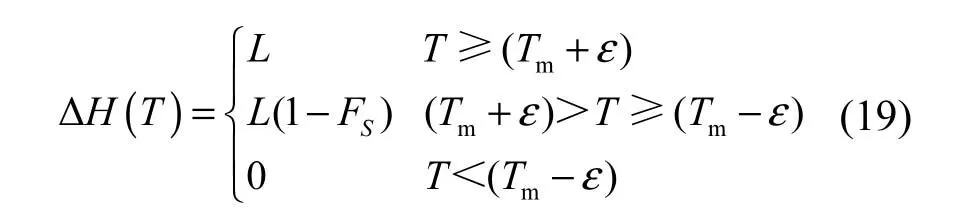
释放潜热可以被看作是只在过渡温度(从液相到固相)范围下释放的显热，因此潜热热容可以定义为

改进后的热容公式为

2 数值模拟

2.1 材料属性

本文模拟初始温度为293K、直径为3.2mm的蒸馏水液滴撞击温度为268K和253K的不锈钢板面，空气为气相．在模型中，空气的温度设置为与不锈钢板面的温度一致，且均低于蒸馏水的冻结温度.材料的基本性质见表1．

表1 空气、蒸馏水、不锈钢板的基本性质Tab. 1The basic properties of air，distilled water and stainless steel plate

2.2 参数与变量

由于模型中液滴存在相变情况，因此需要加入额外的源项来控制相变．在模型中加入的控制变量如表2所示．

模型建立的过程中需要进行全局定义的与模拟过程相关的参数如表3所示．

表2 相变控制变量Tab. 2 Variables in the phase change control equation

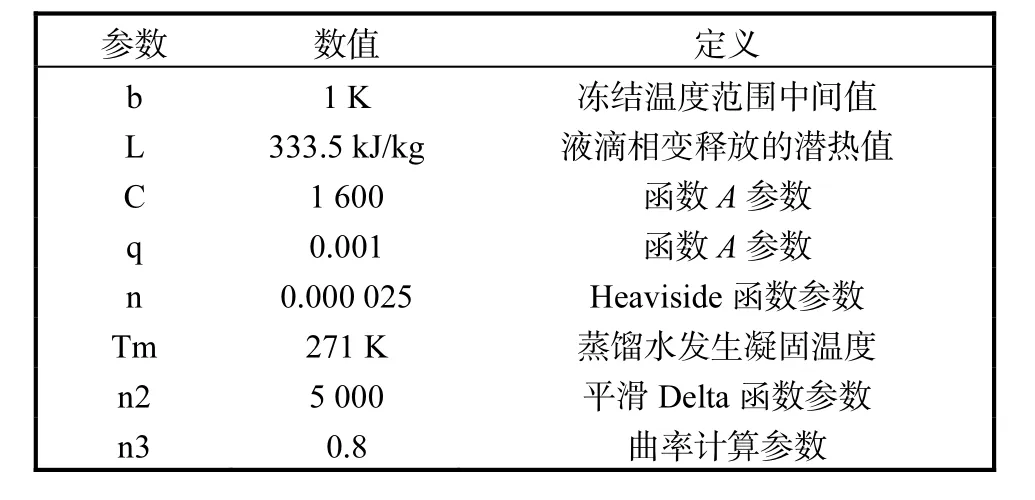
表3 全局定义参数Tab. 3 Globally defined parameters

2.3 模拟过程

利用He等[17]改进的经验公式，计算20℃的蒸馏水液滴在板面上发生附着或破碎与反弹之间的临界韦伯数，可以得到临界撞击速度为2.08m/s，若撞击速度大于临界速度，液滴发生附着或破碎，反之液滴发生反弹．喷雾冷冻干燥箱中的温度可以控制在269～233K．故设置液滴分别从H＝100、250、500mm高度下落，撞击温度为253K和268K的不锈钢板面，对应撞击速度分别为1.4、2.2、3.1m/s．

模拟采用美国COMSOL公司的COMSOL Multiphysics 4.2软件中“流体流动”模块下的“两相流水平集物理场”与“传热”模块下的“流体传热物理场”耦合．考察的是撞击后的液滴铺展直径以及发生相变的过程，因此计算区域选择为包含1个液滴的流体区域．设置环境与板面温度相同，因为空气传热系数较小且下落时间较短，为简化计算假设液滴下落过程中液滴温度不受影响．由于液滴呈球形结构并且板面相对液滴无限大，故将整个液滴与板面简化为二维轴对称模型．计算区域的初始设置见图1．

图1 液滴在板面铺展的计算区域设置Fig. 1Computational domain of droplet spreading on the plate

由于相变过程主要发生在液滴内部以及板面上，且初始界面为液滴边界，因此在划分网格的过程中需要在这些关键界面处将网格细化，如图2所示．在划分网格后，进行求解器设置，对模型进行“相初始化”求解和“瞬态求解器”求解．

图2 液滴在板面铺展的网格划分Fig. 2 Meshing of droplet spreading on the plate

3 模拟结果与讨论

3.1 板面温度对液滴撞击板面的影响

图3(a)和图3(b)为从100mm高度下落液滴分别撞击温度为268,、253K板面时的液滴铺展过程，图4为相应的液滴铺展直径的对比．从图4可以看出：对于同一下落高度，268K对应液滴的最大铺展直径要大于253K的最大铺展直径，且在碰撞板面后，268K对应的液滴与253K对应的液滴相比回缩更快，说明268K不足以使液滴在板面上快速冻结，从而液滴铺展的直径更大，回缩也更明显；而从253K的铺展直径可以看出，液滴达到最大铺展直径后，回缩速度比较慢，说明板面的低温使液滴与板面接触部分产生了凝固现象，减缓了液滴由于表面张力造成的回缩现象．

图3 液滴铺展过程模拟图Fig. 3 Simulated droplet spreading process on the cold plate

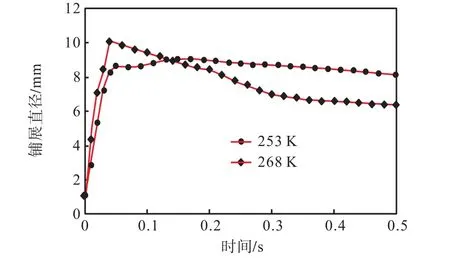
图4 不同冷板温度下液滴铺展直径(H＝100mm)Fig. 4 Droplet spreading diameter under varying cold plate temperatures(H＝100mm)

3.2 撞击高度对液滴撞击板面的影响

图3(b)、图3(c)和图3(d)是不同高度下落的液滴撞击温度为253K板面的液滴铺展过程．从图中可以看出：液滴在碰撞板面后开始铺展，液滴直径逐渐增大，在此过程中凝固阻碍液滴充分展开；撞击高度大时，液滴的铺展直径也相应增大．

从图5可以看出：对于同一板面温度(253K)，不同撞击高度对应的最大铺展直径也不相同，对于从100mm高度下落的液滴，其最大铺展直径为9.1mm；对于250mm高度下落的液滴，其最大铺展直径为12.5mm，铺展到最大直径的时间最短；而对于从500mm高度下落的液滴，其最大铺展直径为14.6mm，铺展到最大直径的时间较长．这是因为液滴的下落高度越高，撞击速度增大，液滴具有了更高的撞击能量．对于253K的板面温度，液滴在回缩过程中也在不断固化，虽然液滴随下落高度增加具有更大的动能，但是固化过程阻碍其回缩到较小直径；液滴回缩的趋势表明，更大高度的撞击会最终造成液滴沉积直径的增大．

图5 不同撞击高度下液滴铺展直径(T＝253K)Fig. 5Droplet spreading diameter under varying impact heights(T＝253K)

3.3 最大铺展直径的模拟结果与实验值的对比

液滴在板面上的铺展面积(最大铺展直径)是研究冷冻沉积时的重要参数，将模拟结果的最大铺展直径值与Xu等[5]的实验值进行对比，结果见表4．可以看出，本文采用的模型与实验值的吻合性较好．

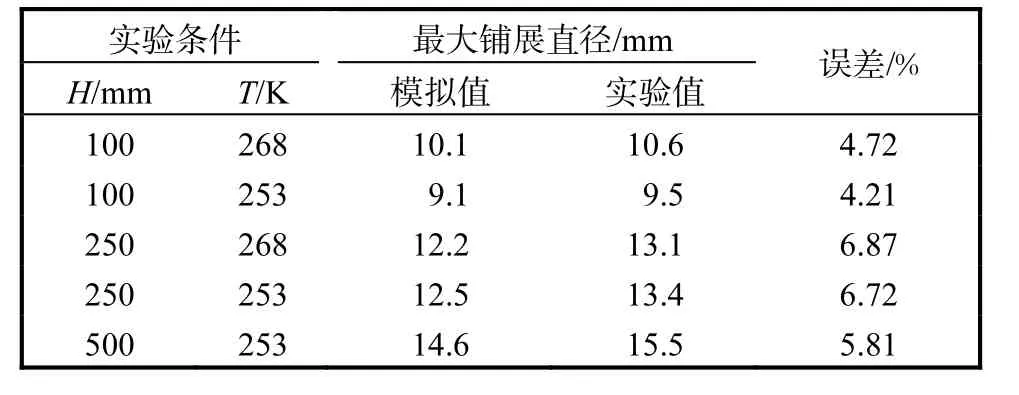
表4 最大铺展直径模拟值与实验值Tab. 4Simulated and experimental value of maximum spreading diameter

4 结 语

本文利用COMSOL Multiphysics 4.2软件的多物理场耦合功能，使用两相流水平集与传热物理场相结合的方法，建立了水平集方法的固化模型，对蒸馏水单液滴撞击水平冷板面的铺展和冻结固化进行了模拟．使用基于温度的热传导方程代替焓值方程，加入熔化潜热修正了热容源项，可以解决低黏度、低密度单液滴(蒸馏水)撞击水平冷板面的固化问题．

模拟对比了蒸馏水液滴在不同撞击高度以及不同温度板面产生的相变情况，发现随着撞击高度的增大液滴的最大铺展直径增大，最终造成液滴沉积直径的增大；而板面温度越低，液滴产生固化现象越明显，其回缩过程越缓慢，回缩程度越小．

最大铺展直径的模拟值与实验值吻合较好，误差小于10%；撞击过程中，撞击高度对液滴的铺展和固化的影响较明显．

［1］ Rogers S，Wu W D，Saunders J，et al. Characteristics of milk powders produced by spray freeze drying[J]. Drying Technology，2008，26(4)：404–412.

［2］ Leuenberger H，Plitzko M，Puchkov M. Spray freeze drying in a fluidized bed at normal and low pressure[J]. Drying Technology，2006，24(6)：711–719.

［3］ Yeom G S，Song C S. Experimental and numerical investigation of the characteristics of spray-freeze drying for various parameters：Effects of product height，heating plate temperature，and wall temperature[J]. Drying Technology，2010，28(2)：165–179.

［4］ Maa Y F，Ameri M，Shu C，et al. Influenza vaccine powder formulation development：Spray-freeze-drying and stability evaluation[J]. Journal of Pharmaceutical Sciences，2004，93(7)：1912–1923.

［5］ 徐庆，耿县如，李占勇. 喷雾冷冻干燥对颗粒产品形态的影响[J]. 化工进展，2013，32(2)：270–275.

［6］ Xu Qing，Li Zhanyong，Wang Jin，et al. Characteristics of single droplet impact on cold plate surfaces[J]. Drying Technology，2012，30(15)：1756–1762.

［7］ 徐庆，李占勇，王瑞芳，等. 单液滴撞击球形表面的涂覆效果[J]. 天津科技大学学报，2013，28(1)：50–54.

［8］ Anandharamakrishnan C，Gimbun J，Stapley A G F，et al. Application of computational fluid dynamics(CFD) simulations to spray-freezing operations[J]. Drying Technology，2010，28(1)：94–102.

［9］ 耿县如，徐庆，李占勇，等. 喷雾冷冻法单个液滴冻结过程模拟[J]. 化工进展，2012，31(5)：981–986.

［10］ Pasandideh-Fard M，Bhola R，Chandra S，et al. Deposition of tin droplets on a steel plate：Simulation and experiments[J]. International Journal of Heat and Mass Transfer，1998，41：2929–2945.

［11］ Voller V R，Markatos N C，Cross M. Techniques for accounting for the moving interface in convection/diffusion phase change[M]//Lewis R W，Morgan K. Numerical Methods in Thermal Problems. Swansea：Pineridge Press，1985：595–609.

［12］ Voller V R，Markatos N C，Cross M. Solidification in convection and diffusion[M]//Markatos N C，Tatchell D G，Cross M，et al. Numerical Simulations of Fluid Flow and Heat/Mass Transfer Processes. Berlin：Springer，1986：425–432.

［13］ Voller V R，Cross M，Markatos N C. An enthalpy method for convection/diffusion phase changes[J]. International Journal for Numerical Methods in Engineering，1987，24(1)：271–284.

［14］ Voller V R，Prakash C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems[J]. Journal of Hat and Mass Transfer，1987，30(8)：1709–1719.

［15］ Marin T L. Solidification of a liquid metal droplet impinging on a cold surface[C]//Proceedings of the COMSOL Users Conference. Trondheim，Norway：COMSOL AS，2006：1492-1–1492-8.

［16］ Sussman M，Smereka P，Osher S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Physics，1994，114：146–159.

［17］ He Zheng，Gao Ye，Gu Xuan，et al. Investigating a droplet-wall collision model[J]. Journal of Harbin Engineering University，2009，30(3)：267–270.

责任编辑：常涛

Numerical Simulation of the Impact of Single Droplet on Cold Horizontal Plate Surface

WANG Jin，LI Zhanyong，XU Qing，WANG Ruifang
(College of Mechanical Engineering，Tianjin University of Science & Technology，Tianjin 300222，China)

In spray-freeze drying(SFD)，freeze deposition of liquid droplets on the equipment walls has become a new challenge to its applications. Based on the previous experimental results of droplet collision with cold horizontal solid plates，a model of a single droplet collision with cold solid plates was established with the combination of the Level Set method and the solidification model to simulate the impacting process of the distilled water droplet(3.2mm in diameter，at 293K)on the stainless steel plate(268K or 253K) from the height of 100mm，250mm and 500mm，respectively. The simulation results of maximum spreading diameter were compared with the experimental data and the errors were less than 10%，which indicates that the model is suitable for dealing with the impact of droplets of low viscosity and low-density on the cold horizontal plate surface.

single droplet；cold plate surface；simulation；level set method；solidification model

TQ051

A

1672-6510(2014)01-0036-06

10.13364/j.issn.1672-6510.2014.01.008

2013–10–07；

2013–11–15

国家高技术研究发展计划(863计划)资助项目(2012AA021303)

王 瑾（1990—），女(满)，陕西人，硕士研究生；通信作者：李占勇，教授，zyli@tust.edu.cn.