锥形辊穿孔机顶头辗轧锥角的精益设计及验证

董少峰，郭继保

（太原通泽重工有限公司，山西太原030032）

锥形辊穿孔机顶头辗轧锥角的精益设计及验证

董少峰，郭继保

（太原通泽重工有限公司，山西太原030032）

建立了锥形辊穿孔机顶头辗轧锥角数学模型，以精确求得锥形辊穿孔机顶头辗轧锥角；并采用有限元法对设计效果进行验证。结果表明：采用穿孔机顶头辗轧锥角的精益设计方法设计的顶头，其轧制的毛管壁厚相对误差在2%～3%，壁厚最大偏差在1%以内，满足API标准要求且达到较高精度。该设计方法为穿孔工具设计软件及工艺控制模型的建立提供数学理论依据，可有效提升企业产品的市场竞争力。

锥形辊穿孔机；顶头；辗轧锥角；精益设计；有限元；壁厚精度

轧制工具的设计直接影响到无缝钢管的生产质量，随着国际市场对无缝钢管加工质量要求的提高，用户也对轧制工具的设计提出了更高的要求。穿孔机顶头的设计直接决定着穿孔的质量，而顶头辗轧锥角直接决定穿孔毛管的壁厚精度，辗轧锥角过大或过小都会引起毛管的壁厚不均，以致影响成品管的质量和精度。

由于国内最初引进的穿孔机均为桶形辊穿孔机，所以国内的许多学者对桶形辊穿孔机进行了大量的研究［1-4］。对于顶头辗轧锥角的计算也停留在桶形辊穿孔机上：文献［3］对桶形辊穿孔机顶头辗轧锥角的计算及合理设计进行了总结和归纳，并提出了空间变形区模型下顶头辗轧锥角的计算方法；文献［4］中所提到的穿孔机顶头辗轧锥角的计算仍为桶形辊穿孔机的经验算法。

近几年来，锥形辊穿孔机以其扩径量大、变形均匀、轧制缺陷少等优势，逐渐占据了穿孔机的主流市场［5-9］。但是，由于辗轧角和送进角的同时存在，给建立工具立体数学模型及精确计算穿孔工具造成一定的困难。国内钢管厂对锥形辊穿孔机顶头辗轧锥角的计算仍套用国外的参数，没有具体的数学模型。

本文主要介绍利用空间坐标变换，建立锥形辊穿孔机的曲面模型，并将轧辊开口度简化为非线性约束优化问题进行求解，最终建立了穿孔机顶头辗轧锥角的数学模型，随后利用有限元对新设计穿孔工具进行数值工艺模拟的过程。

1 计算模型的建立

1.1 轧辊曲面模型的建立

锥形辊穿孔机轧辊平面布置如图1所示。由于顶头辗轧锥角只与轧辊出口段有关，故只需建立轧辊出口段的曲面模型。在标准坐标系oxyz下，轧辊出口端由一段梯形圆锥组成。轧辊标准方程为：

式中，-DH/2-LAcos（α2-αA）≤x≤DH/2+LAcos（α2-αA），-LAsin（α2-αA）≤y≤0，LA为轧辊出口锥长度，αA为轧辊出口锥角，α为轧辊辗轧角，α2= 90°-α+αA，α3为与α有关的几何参数。

图1 锥形辊穿孔机轧辊平面布置示意

利用齐次坐标变换，将轧辊在oxyz坐标系下的曲面模型转换到OXYZ坐标系下，则坐标系oxyz需依次作如下基本变换：oxyz坐标系沿x轴左平移DH/2，DH为轧辊直径；绕z轴顺时针旋转α3；绕y轴顺时针旋转β（送进角）；沿y轴向下平移E/2（图1）。从oxyz坐标系到OXYZ坐标系的坐标变换系数为H［10］。二者的关系可用下式表示：

将求得的x、y、z代入式（1）即可求得轧辊在OXYZ坐标系下的曲面模型：

1.2 轧辊开口度模型的建立

为了定义锥形辊穿孔机顶头的辗轧锥角，必须建立顶头辗轧段轧辊空间实际开口度模型。A-A截面上轧辊开口度如图2所示。由于式（3）中的X已知，所以A-A截面上轧辊的曲线方程可简化成：

图2 A-A截面上轧辊开口度示意

假设A（Y，Z）是轧辊曲线上任意一点，则该点到坐标原点O的距离可表示为：

因此，A-A截面上轧辊开口度可以这样描述：在A-A截面上求轧辊曲线方程到轧制中心线的最短距离R。可以采用如下数学式描述：目标函数R=约束条件F（Y，Z），Y∧0。

此问题为非线性约束优化问题，其求解算法已经比较成熟，不再赘述。以某穿孔机参数为例，编制通用程序，其轧辊开口度计算结果如图3所示。

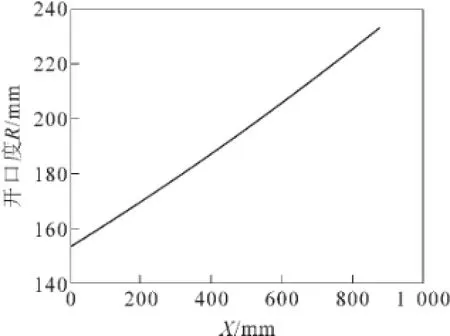
图3 轧辊开口度计算结果

1.3 顶头辗轧锥角的计算

为了保证穿孔机出口毛管的壁厚均匀，必须保证辗轧段DE始终与相对应的轧辊空间开口段BC平行，即DE与轧制中心线所形成的辗轧锥角β1等于BC与轧制中心线所形成的角度β2，如图4所示。

根据确定的开口度，可得到B、C点的坐标值。当顶头的位置和辗轧段长度确定后，顶头的辗轧锥角β1也可确定，为：

2 结果对比

将国外实际生产中部分型号顶头的参数与本模型计算结果进行对比，结果见表1。

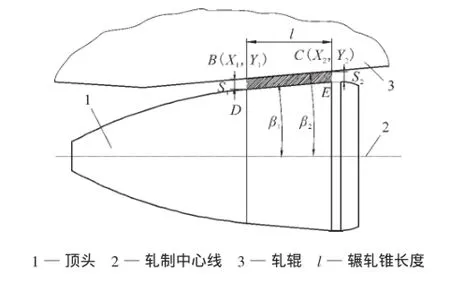
图4 顶头辗轧锥角计算示意

表1 顶头参数对比

从表1可以看出：所选型号顶头辗轧锥角β1的最大误差为0.42%，最小误差为0.01%，模型计算结果与国外顶头参数基本吻合。实际上，由于基本模型、算法及计算精度的差异，并不能说明哪个模型的精度更高；因此，模型的使用效果需通过模拟验证和实际应用验证。

3 模拟验证

随着计算机软/硬件的飞速发展及数学计算方法的不断进步，计算机数值模拟已成功地取代了大部分物理模拟［11］。现以某锥形辊穿孔机为例，采用有限元法对穿孔机轧制工艺进行模拟，以期对顶头辗轧锥角的设计效果进行验证。

锥形辊穿孔机的工艺参数如下：轧辊辗轧角α为15°，送进角β为10°，轧辊出口锥角αA为4.6°，轧辊直径DH为1 500 mm；顶头型号采用350-415-24，相关参数见表1；管坯外径DB为350 mm；毛管外径D为415 mm；毛管壁厚S为24 mm；轧辊转速为80 r/min。锥形辊穿孔机轧制工艺有限元模拟结果如图5所示。

图5 锥形辊穿孔机轧制工艺有限元模拟结果

在有限元模拟过程中网格畸变严重，准确测量壁厚比较困难，所有的有限元模拟结果必须经过数据处理。根据毛管截面输出截面数据点坐标，并拟合成样条曲线，出口毛管截面输出的截面数据点坐标如图6所示，内外轮廓数据点插值如图7所示。

图6 出口毛管截面输出的截面数据点坐标

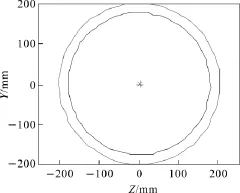
图7 出口毛管截面输出的内外轮廓数据点插值

根据数据点求弧长的三次样条插值原理，利用龙贝格（Romberg）积分法［12］可以计算出口毛管内外轮廓的周长δ。假设毛管内外轮廓由等分的N段圆弧组成，每段圆弧对应的弧度为θ，各圆弧对应圆的半径R1、R2、R3…RN，则内外轮廓的周长δ可以用R1θ+R2θ+R3θ+…+RNθ表示，而内外轮廓的平均直径

根据计算出的出口毛管截面平均直径及圆心，可以计算得到出口毛管的平均壁厚。用5个截面分段截取出口毛管，以计算其平均外径和壁厚，计算结果见表2。

表2 采用有限元模拟得出的毛管外径和壁厚数据

从表2可以看出：壁厚相对误差稳定在2%～3%，壁厚最大偏差理论计算控制在1%以内；采用穿孔机顶头辗轧锥角的精益设计方法设计的顶头，其轧制的毛管壁厚精度满足API标准要求且达到了较高的精度。

对于270-286-39和350-415-63型号顶头的辗轧锥角，国外参数与本模型计算结果误差较大，因此选取这两组顶头计算其毛管壁厚精度，结果见表3。从表3可以看出：与国外顶头计算结果相比，采用本模型计算参数计算的平均壁厚相差不大，但壁厚最大偏差小于国外顶头的。

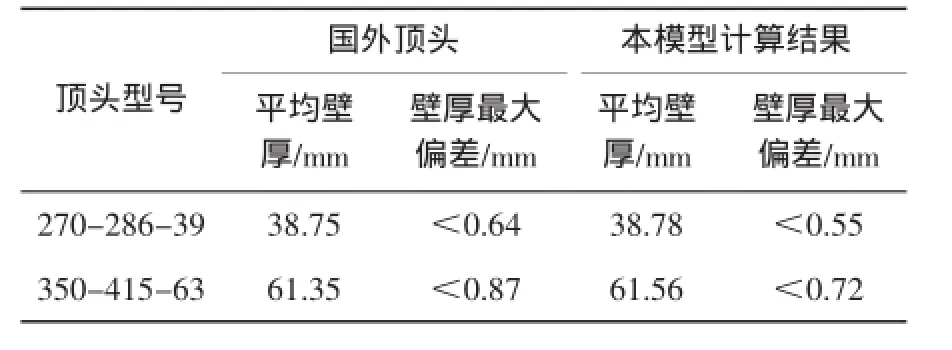
表3 毛管壁厚计算结果对比

当然，毛管壁厚精度控制与现场测量及操作水平也有很大关系，理论计算精度的实现还需要严密科学的操作步骤和方法，而该锥形辊穿孔机顶头辗轧锥角数学模型的现场使用效果也需进一步验证。

4 结语

本研究建立了锥形辊穿孔机顶头辗轧锥角数学模型，从工具间的几何关系入手，精确求得锥形辊穿孔机顶头辗轧锥角，并采用有限元法对设计效果进行验证。验证结果表明：采用本方法设计的顶头，可确保毛管的壁厚精度。该计算方法同时也为穿孔工具设计软件及工艺控制模型的建立提供了数学理论依据。

［1］朱景清，吕庆功，王红炜，等.关于鼓形穿孔机和锥形穿孔机的讨论［J］.钢管，2010，39（1）：30-34.

［2］金如崧.斯蒂弗尔穿孔机［J］.钢管，1999，28（5）：48-57.

［3］詹才俊.穿孔顶头辗轧段锥角的计算及合理设计［J］.钢管，1990，19（4）：22-25.

［4］成海涛.无缝钢管缺陷与预防［M］.成都：四川科学技术出版社，2007：118-119.

［5］殷国茂.中国钢管50年［M］.成都：四川科学技术出版社，2004.

［6］殷国茂.中国钢管飞速发展的10年［M］.成都：四川科学技术出版社，2009.

［7］田党，李群.孔腔离层与扭转变形——关于二辊斜轧桶形辊穿孔机与锥形辊穿孔机的讨论［J］.钢管，2012，41（6）：63-68.

［8］冀文生.太原通泽重工有限公司锥形穿孔机实现出口［J］.钢管，2011，40（5）：68.

［9］万本振，韩建元，汤智涛.基于MATLAB锥形辊穿孔机开度值的计算分析［J］.钢管，2012，41（2）：53-55.

［10］董少峰，郭继保，魏利明.锥形穿孔机导板设计的模型建立［J］.机械管理开发，2009，24（1）：91-92.

［11］尹元德，李胜袛.AutoCAD在有限元模拟连轧管壁厚测量中的应用［J］.工程图学学报，2006（1）：13-18.

［12］杜廷娜，徐元.三次样条插值曲线弧长算法与工程实现［J］.渝州大学学报：自然科学版，1998，15（2）：40-42.

Lean Design and Verification of Plug Toe Angle of Cone-type Piercer

DONG Shaofeng，GUO Jibao
（Taiyuan Tongze Heavy Industry Co.，Ltd.，Taiyuan 030032，China）

A mathematic model of the plug toe angle of the cone type piercer is established in order to precisely get the plug toe angle determined.And the design verification is conducted with the finite element（FE）method.As a result，it is identified that using the plug toe angle of the piercer as designed with the lean design method will be able to produce shells with wall thickness relative error as 2%～3%，and maximum deviation within 1%，being up to applicable API specification，and having rather high accuracy.The said design method provides relevant mathematic theoretic basis for establishing the tool design software，and the process control model for the piercing mill，so as to further sharpen the product competitive edge of the company.

cone type piercer；plug；toe angle；lean design；finite element；wall thickness accuracy

TG333.8

B

1001-2311（2014）06-0068-04

2014-05-14；修定日期：2014-10-09）

董少峰（1978-），男，硕士，工程师，长期从事轧钢工艺设计及模拟仿真工作。