毛管入口流量估算方法与验证
2019-07-18段晓辉牛文全
段晓辉,牛文全
(西北农林科技大学水土保持研究所,陕西 杨凌 712100)
滴灌系统管网水力学计算是滴灌工程设计的基础。近年来,对滴灌系统水力学解析进行了大量的研究,但不同研究采用的计算方法不同,考虑的影响因素差异较大。如Myers等[1]和Wu等[2]利用Bernoulli方程和Darcy-weisbuch公式,采用多孔系数等方法对管道水力学解析进行近似简化计算。Warrick[3]提出了一种选择处理的滴灌毛管水力计算设计方法。Valiantzas J D[4-7]以分析逼近的方法模拟毛管进口水头与平均水头的关系及水头损失与能耗的关系,进行了毛管的优化设计。魏秀菊[8]分析了平坦地形微灌田间管网设计中单元内允许压差在支、毛管中合理分配理论。张林等[9]通过分析不同坡度条件下,毛管水头损失变化规律,推导出了考虑地面坡度及水力偏差的单毛管流量偏差率计算公式。张国祥等[10-12]通过研究提出来适应田面地形的滴灌系统滴头设计水头计算公式。郑纯辉[13]提出了利用有限元法,设计出符合灌水器平均相对流量和灌水均匀度要求的相应支管单元操作压力水头。鞠学良[14]应用微灌管网水力学知识及数学方法,构建了均匀坡毛管和灌水小区及非均匀坡毛管的水力解析模型。张志新[15-16]通过对滴灌毛管进行水力学解析时发现,有限元法计算结果准确,但是计算量和存储量大。王新坤[17-18]以微灌系统田间管网水力解析与节约成本的优化设计为目标,提出利用遗传算法理论进行微灌系统田间管网水力学解析方法。白丹和党志良[19]提出了不规则田面微灌管网优化设计方法。上述这些方法虽然都基本可以确定滴灌管网系统的水力参数,但计算过程普遍比较复杂,需要多次试算才能确定近似值。康跃虎[20]通过研究提出了利用多项式表示毛管入口压力与入口流量的关系,并将其命名为毛管流量公式。利用多项式表示毛管入口压力与入口流量的关系,虽然计算结果精度较高,但拟合过程较为复杂。熊国武[21]研究发现,毛管入口水头和入口压力的关系可以用幂函数表示,这种表示方法拟合的毛管入口水头和入口流量关系式拟合度高,误差较小,计算方便,但是对于参数a、b的影响因素和确定方法缺乏进一步的研究。
Q=aHb
(1)
式中,Q为毛管入口流量(L·h-1);H为毛管入口工作水头(m);a,b为拟合系数。
以往研究中所采用的毛管流量计算方法较为复杂且计算量大,不便于实施。本研究以毛管结构参数为基础,考虑各影响因素的综合作用,建立毛管入口流量估算模型,以期为简化滴灌系统管网水力学解析过程,为简化滴灌设计提供理论依据和参考。
1 材料与方法
1.1 试验设计与方法
1.1.1 毛管水力参数的试验测定方法与装置 试验装置如图1所示,试验仪器设备主要包括水泵、水箱、压力调节装置、精密压力表(0.2级)、秒表、雨量筒、电子天平等。水泵为系统提供额定的工作压力,试验采用内镶式滴灌带,铺设长度为60 m,滴头间距为0.3 m,外径为16 mm,额定流量为2.1 L·h-1,经测定滴头流量系数及流态指数分别为0.5035和0.5880,滴灌带固定在试验台上,沿试验台水平铺设。
毛管入口工作水头设置为1、2、3、4 m和5 m。试验开始,通过调节入口处的球阀门控制毛管入口工作水头值,待压力稳定后,沿毛管入口等距选取20个滴头,利用量杯收集相应滴头出水,最后用称重法计算滴头流量。每次试验进行15 min,重复2次,随后调节毛管入口工作水头,并重复上述试验步骤。
1.1.2 毛管水力性能的计算方法 毛管水力参数性能采用退步法确定,如图2所示,沿毛管末端滴头开始编号,图中:ΔHn为毛管各管段的水头损失(m);Qn为毛管各管段流量(L·h-1);s为滴头间距(m);hn为各滴头的工作水头(m);qn为各滴头的流量(L·h-1)。
根据质量守恒定律,毛管各管段流量由式(2)计算:
qi=Qi+1-Qi
(2)
式中,qi为第i个滴头流量(L·h-1);Qi、Qi+1为第i、i+1管段流量(L·h-1)。
毛管各管段的总水头损失由式(3)计算[22-23]:
(3)
式中,ΔHi为毛管第i个管段总水头损失(m);a为水头损失扩大系数;Qi为毛管第i个管段的流量值(L·h-1);s为滴头间距(m);d为毛管直径(mm);f、m、b分别为摩阻系数、流量指数、管径指数;其余符号意义同上。
由压力递推原理,毛管各滴头工作水头由式(4)计算:
hi=hi-1+ΔHi
(4)
式中,hi,hi-1分别为毛管第i个和第i-1个滴头的工作水头(m);其余符号意义同上。

图1 试验装置示意图Fig.1 Schematic diagram of experimental device

图2 毛管水力计算模式示意图Fig.2 Schematic diagram of capillary hydraulic calculation
毛管入口工作水头及入口流量分别由式(5)和式(6)计算:
H=hn+ΔHn
(5)
Q=Qn-1+qn
(6)
式中,H为毛管入口工作水头(m);Q为毛管入口流量(L·h-1);其余符号意义同上。
1.1.3 毛管入口流量估算模型的建立 利用Excel RAND函数,在给定毛管各参数范围内随机各生成300组随机数,即每个毛管结构参数为300个水平,采用随机组合方式作为特定毛管结构参数,毛管各结构参数具体范围如表1所示。获取每组毛管入口工作水头与入口流量时,将毛管入口工作水头H设置为1 、1.5 、2 、…、14.5 m和15 m等共30个水平,利用退步法毛管水力学解析原理计算不同毛管结构参数所对应的毛管入口工作水头与入口流量值,最后利用最小二乘法计算拟合系数a和拟合系数b。
1.1.4 毛管入口流量估算模型的验证 验证试验共设置8个处理,每个处理下毛管入口工作水头设置为4、6 m和8m,毛管沿试验台水平铺设(i=0),具体试验处理如表2所示,利用上述1.1.1试验方法对给定毛管及毛管入口工作水头下的毛管入口流量进行测定。
1.2 数据处理
采用Microsoft Excel 2013软件处理数据,用SPSS 22.0统计软件对拟合系数与毛管结构参数进行相关性分析及方程拟合,用Origin 8.0软件绘图。

表1 模拟参数输入列表

表2 试验处理
2 结果与分析
2.1 毛管入口流量退步法计算结果的检验
当毛管入口工作水头H=1、2、3、4 m和5m时,毛管入口流量实测值与利用退步法毛管水力学解析方法计算结果如表3所示。可以看出,不同毛管入口工作水头下,毛管入口流量实测值与利用退步法毛管水力学解析方法计算值的最大相对误差为11.09%,最小相对误差仅为0.04%,平均相对误差为3.35%。由于在使用退步法毛管水力学解析方法计算毛管入口流量时,没有考虑灌水器制造偏差、滴头堵塞等因素,导致毛管入口流量实测值与计算值会产生一定的误差,经过验证发现两者之间平均相对误差较小。因此,当毛管入口工作水头一定时,利用退步法毛管水力学解析原理计算毛管入口流量具有较高的精度。
2.2 毛管入口流量估算方法
对随机生成的300组不同结构参数毛管与相对应计算得到的拟合系数a和拟合系数b分别进行Pearson相关性分析(表4),可以看出,毛管长度、毛管铺设坡度、滴头间距和流量系数显著影响拟合系数a,而毛管管径和流量指数与拟合系数a没有显著的相关性;毛管铺设坡度和流态指数显著影响拟合系数b,而毛管长度、滴头间距、毛管管径和流量系数与拟合系数b没有显著的相关性。其中,滴头间距与拟合系数a的相关性最高,相关系数达到-0.726,流量系数、毛管长度和毛管铺设坡度次之,说明滴头间距是影响拟合系数a最为重要的因素;毛管铺设坡度与拟合系数b的相关性最高,相关系数达到0.840,流态指数次之,说明毛管铺设坡度为影响拟合系数b最为重要的因素。
利用模拟生成的300组毛管结构参数分别与毛管流量公式中拟合系数a和拟合系数b进行回归拟合,可分别建立相应毛管结构参数与拟合系数a和b的关系式,即毛管入口流量估算模型为:
式中,l为毛管长度(m);s为滴头间距(m);k为流量系数;i为毛管铺设坡度;d为毛管管径(mm);x为流态指数;其余符号意义同上。
由方差分析结果可知,Fa=9436.17>F0.01(6, 293)=2.80,Fb=7203.99>F0.01(4, 295)=3.32,回归方程均达到极显著水平。拟合系数a和拟合系数b采用退步法拟合值与模型估算值散点图(图3)显示,拟合系数a和拟合系数b的理论值与模拟值决定系数R2分别为0.9949和0.9899,其理论值与模拟值平均相对误差分别为2.30%和0.70%,相对误差较小,表明拟合方程的拟合效果较好。
2.3 毛管入口流量估算模型的检验
为了检验毛管流量估算模型参数的适应性,通过检验分析得到拟合系数a和拟合系数b实测值与估算值,其误差如表5所示。拟合系数a的平均相对误差为5.97%,拟合系数b的平均相对误差为0.30%。拟合系数a的平均相对误差有所增大,拟合系数b的平均相对误差有所减小,这是由于在利用最小二乘法拟合毛管流量公式时,拟合系数a和拟合系数b随毛管入口工作水头范围的变化会发生波动,当毛管入口工作水头范围普遍较大时,拟合系数a值会明显的增大,导致模型的拟合误差偏大,因此,选择合理的毛管入口工作水头范围进行拟合分析,可以有效地降低模型误差。

表3 不同毛管入口工作水头下入口流量实测值与计算值

表4 拟合系数a、b与毛管各参数的相关性
注:**表示相关性在P<0.01水平上差异显著。
Note: ** indicates that the correlation is significant atP<0.01 level.

图3 拟合系数a和拟合系数b退步法拟合值与模型估算值散点图Fig.3 Plots of regression coefficient fitting values and model estimation values of fitting coefficients a and b
当毛管入口工作水头为4、6 m和8 m时,毛管入口流量实测值与毛管流量估算方法的估算值误差如表6所示。毛管入口流量实测值与估算值最大相对误差为11.65%,平均相对误差为3.79%,误差较小,说明本文建立的毛管流量估算模型具有较高的精度及适应性。
3 结 论
不同毛管入口工作水头下,毛管入口流量实测值与利用退步法毛管水力学解析方法计算值的最大相对误差为11.09%,最小相对误差仅为0.04%,平均相对误差为3.35%。毛管长度、毛管铺设坡度、滴头间距和流量系数显著影响拟合系数a,毛管铺设坡度和流态指数显著影响拟合系数b。
经过拟合分析建立相应毛管结构参数与拟合系数a、拟合系数b的回归方程。通过验证发现,当毛管入口工作水头为4、6 m和8 m时,通过实测得到的毛管入口流量值与本文建立的毛管流量估算模型计算毛管入口流量值平均相对误差为3.79%,说明本文建立的毛管入口流量估算模型具有较高精度及较强的适应性。

表5 拟合系数a和拟合系数b实测值与估算值误差表
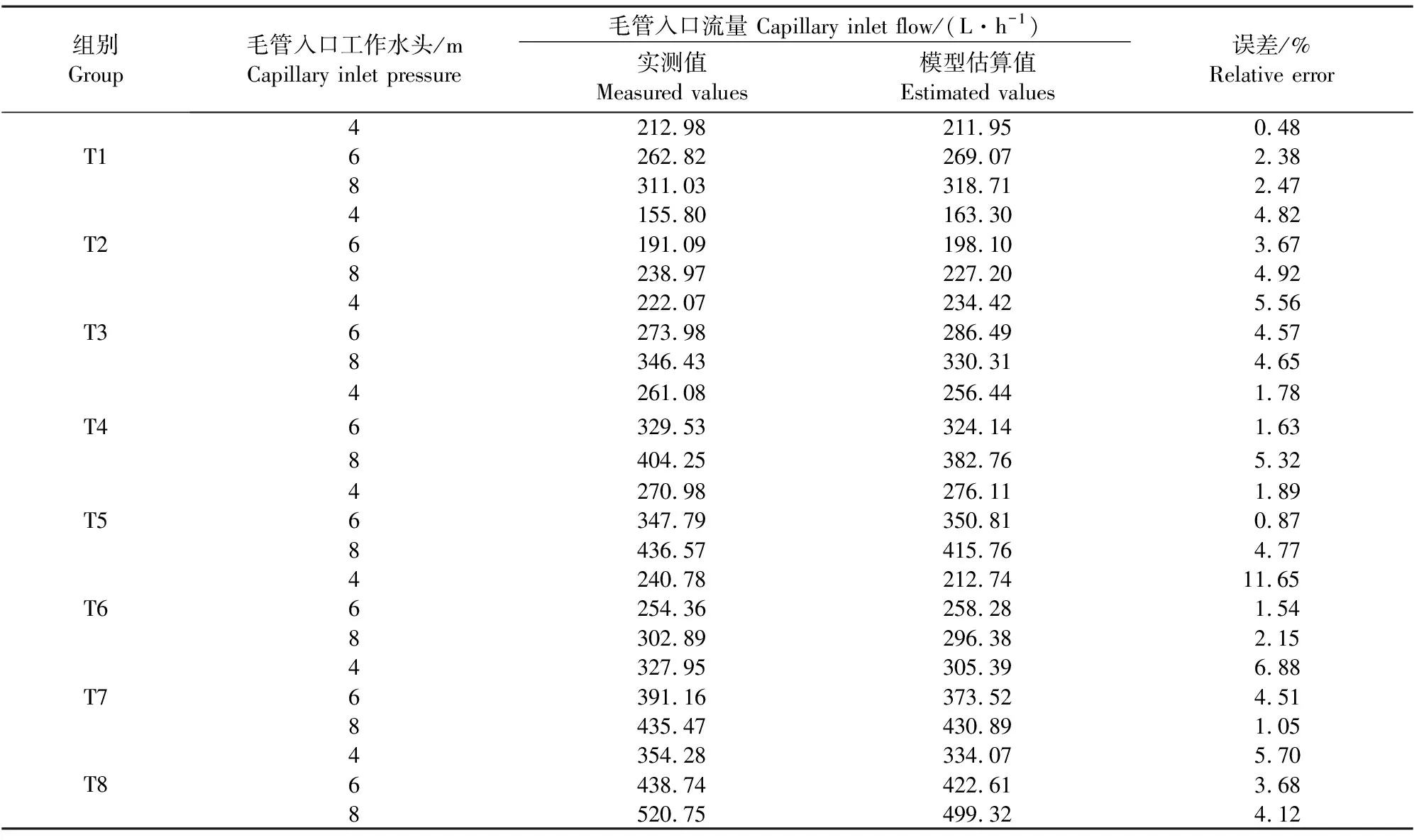
表6 毛管入口流量实测值与估算值误差表
