船舶装载对初稳性影响的实验教学模型

任 凯， 浦金云， 李 营

(海军工程大学 动力工程学院，湖北 武汉 430033)

0 引 言

倘若能够为学生提供一个简捷的平台，学生通过实际动手完成船模实验[1-2]，感受载荷种类、载荷变动对船舶稳性的影响，并根据实验结果与理论计算分析比较完成重要内容的强化训练，对提高学生分析问题、理解要点十分有益[3]。船舶装载对初稳性影响的实验教学模型提供了这样的平台。该模型采用了不锈钢材质，包括船模、水槽、砝码、配重载荷等部分，平台具有简洁轻便、可靠耐用、功能全面的特点，能够在实验教学过程中帮助学生生动的理解相关问题[4-5]。

1 模型实验验证的理论基础

1.1 船舶装载对初稳性影响实验验证的基本方法

运用船模开展“船舶装载对初稳性影响的实验教学”关键在于让学生通过实验验证掌握载荷种类不同、位置不同对船舶稳性的影响效果。本实验装置具备了开展相关试验的基本条件，验证船模稳性影响可以通过船模的横摇周期来判定。通过测定船模的横摇周期，运用经验公式计算船模当前的初稳度[6-8]。

1.2 船模横摇周期稳定性判定

船模实验验证的理论基础在于判定实验模型在静水阻尼作用下，横摇周期的稳定性问题。也就是说，船模初稳度可以进行实验验证，关键在于横摇过程中横摇周期不随船模横摇摆幅而变化[9]。根据船舶静力学的相关理论[10]，其横摇运动在数学上可近似的描述为齐次二阶常微分方程。船模小幅自由横摇时，可以认为横摇阻尼为线性规律[11-13]，横摇运动方程为：

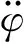
(1)

式中：Jφφ为横摇转动惯性矩(kg·m2)；ΔJφφ为附加转动惯性矩(kg·m2)；Nφφ为横摇阻尼；D为排水量(m3)；h为横稳度(m)。

(2)

(3)

φ(t)=φae-νφφtcos(nφ1t-εφ)

(4)

此时，在静水阻尼的作用下，船模的横摇周期可表示为：

(5)

(6)

由式(6)可得经验公式[6]：

(7)

式中：c是船型系数，一般船舶通常为0.37～0.45，对于矩形实验船体模型，c取值为0.5；B是船体的宽度[14]。因此，运用横摇周期判定船模的初稳度，并以此为基础设计相关的实验装置，研究船舶装载对初稳性的影响问题是可行的。

2 实验教学模型设计

2.1 模型实验验证的主要理论问题

船舶装载对初稳性的影响与载荷的种类有关，载荷的位置变化会对船舶初稳性带来影响，而固体载荷与液体载荷对船舶初稳性的影响亦不相同，在理论上移动和装卸固体载荷时，考虑到船舶纵稳度远大于横稳度，横稳度的变化则是关系船舶安全的主要衡量指标，教学过程中重点强化学生对横稳性的理解；导移和装卸液体载荷时，液体载荷对船舶初稳性的影响除了等量的固体载荷的影响外，还存在着自由液面的影响。这些理论问题衍生出“载荷重心位置变化的幅度与稳性的关系如何”，“中性面的位置究竟在哪里”，“自由液面对船舶稳性的影响结果究竟有多大”等一系列需要“证实”的问题，学生初次接触此类问题时，对于上述内容的理解存在着实验辅助学习的刚性需求[15]。表1中列出了本实验教具开展验证的有关船舶静力学中船舶装载和载荷变动的相关理论问题与计算方法。

2.2 实验目的

对于船舶而言，稳性是重要的安全性指标，在船体上没有一个具体的刻度来标志它的大小，但它确是客观存在的，稳度的降低会影响船舶的航行安全。船舶装载对初稳性影响的实验教学模型主要用于学员掌握2.1章节中所涉及的理论问题，其结果是与稳度变化Δh有关的量。该实验教学模型能够在功能上满足以下实验保障条件：①移动固体载荷对船舶稳性影响的验证；②装卸固体载荷对船舶稳性影响的验证；③装卸相同质量的固体载荷和液体对船舶稳性影响之比较；④装载相同质量的液体载荷时，自由液面面积不同对船舶稳性影响之比较。

表1 船舶装载和载荷变动的相关理论问题与计算方法

2.3 实验模型的材料与结构设计

根据上述功能需求，考虑到模拟船体一般性原理结构，模型模拟了船舶的舱段结构，采用方舱体构造，使用201不锈钢板材焊接制成。分为7个分体，包括主船体模型、2个大舱模型和4个小舱模型。主体结构如图1所示。

实验模型为长60 cm，宽12 cm，型深10 cm，在船模中部距离舱底3 cm处和船模中部距基线12 cm处各设置载物平台1个，平台中心安装固定杆，240 g砝码作为重物可在平台和液舱间移动。船模两端距离基线7 cm高度各设置平台1个，可实现12 cm×20 cm×3 cm液舱和2个6 cm×20 cm×3 cm液舱轮换布置，用于模拟不同大小的自由液面。材料密度约为7 850 kg/m3，板厚1.5 mm，实验模型金加工后，结构如图2所示。

图1 实验模型结构图

图2 实验教学模型

2.4 实验模型参数的理论计算

理论计算过程中，计算船模初稳性通过下式完成。

h=zc+r-zg

(8)

该实验模型的重量、浮心、重心、横稳定中心半径、初稳度等基本参数需进行计算，由于该实验模型形态规则，因此不难准确计算上述模型的参数，且计算结果可作为实验教学过程中开展典型工况模拟的理论数据。根据船模的物理特性以及合力距定理[7]，在典型实验状态下，船模的状态参数计算采用如下表2所示方法完成，考虑到计算方法的通用性，表2中仅列出了空船状态下船模参数的计算结果，其他典型状态不做赘述。

表2 空船船模参数计算表

注：表中标注*号的单位是cm

3 典型条件下的实验模型性能分析

运用该实验模型开展实验教学，目的在于加深学生对载荷变动与船舶稳性关系之间的理解。通过实际动手完成载荷变动实验，计算模型的稳度变化情况，在实验过程中，模型的稳度通过式(7)的方法计算。

3.1 移动固体载荷对船模初稳度影响的实验过程

空船无液舱状态下船模的稳度为1.30 cm，此时在船模顶部平台上加载240 g砝码后，此时的船模的稳性理论结果为0.67 cm。实验视频剪辑后可知船模的横摇周期约为1.52 s，经式(7)计算后，实验计算结果为0.62 cm。当载荷移动到船中平台上，此时理论计算结果为1.24 cm，实验测算结果为1.19 cm。通过实验结果计算与理论分析的结果比较，在移动载荷的实验条件下，理论分析结果与实验测算结果误差在3.22%～7.46%，这一实验结果是可以满足课堂教学的实验条件的。由于船模船中平台所在位置在水线面附近，这一结果同样可以帮助学生验证“中性面”这一理论问题，也就是说在中性面上增减载荷对船舶的稳性影响较小。图3和图4分别是载荷变动前后的实验过程截图。

0.29s0.96s1.81s2.56s3.44s4.08s

图3 船模顶部平台加载240 g固体载荷后的实验过程

图4 船模船中平台加载240 g固体载荷后的实验过程

3.2 装载相同质量的固体载荷和液体对船模稳性影响的实验过程

为了验证等质量的固体载荷和液体载荷对船模初稳度的影响，实验中在空船顶部平台布置了大液舱，大液舱中部，底面形心位置安装固定金属杆一枚，砝码可固定在金属杆上(如图3所示)。船模的初稳度实验分两次进行，第一次通过烧杯向大液舱内注入240 mL水，第二次倒掉液舱内水，在大液舱内的固定杆上安装240 g砝码，分别进行横摇周期测试。

当大液舱内加水后，此时的船模的稳性理论结果为0.30 cm。实验视频剪辑后可知船模的横摇周期约为2.36 s，实验计算结果为0.26 cm。当载荷变化为等质量的砝码后，此时理论计算结果为0.77 cm，实验测算结果为0.69 cm。理论分析结果与实验测算结果误差在10.38%～13.33%，这一结果基本满足实验验证的需求。图5和图6分别是载荷变动前后的实验过程截图。

1.92s3.25s4.58s5.71s6.87s8.08s

图5 船模前舱内加载240 mL水后的实验过程

图6 船模前舱内加载240 g固体载荷后的实验过程

3.3 自由液面面积不同对船模稳性影响的实验过程

为了验证自由液面对船舶初稳度的影响作用，实验设置了代换液舱，用于验证改变自由液面面积对船舶初稳度的影响。实验中，用两个小液舱对船模的大液舱进行替换，小液舱总容积近似等于大液舱的容积。由于在高处增加了液舱隔板，增大的载荷总重量约为71 g，高处加载后对船模稳性影响非常剧烈，替换后需要对实验模型进行稳度修正，使得此时未加液体载荷条件下的船模初稳度与船模中安装大液舱情况下的初稳度相近，采用的方法是在底部加装压载铁板。

当两个小液舱内各加水120 mL并稳定平衡后，此时的船模的稳性理论结果为0.66 cm。实验视频剪辑后可知船模的横摇周期约为1.55 s，实验计算结果为0.60 cm。理论分析结果与实验测算结果误差约为9.09%，这一结果可以满足实验验证的需求，而且通过与3.2中大自由液面的稳度计算结果进行比较，能够较好地验证减小自由液面的宽度，并进行分割，可以有效地提高船舶初稳度这一结果。图7是液舱变动后的实验过程截图。

1.58s2.29s3.12s4.00s4.75s5.60s

图7 船模前舱两个小液舱内各装载120 mL水后的实验过程

4 结 语

本装置在开展船舶装载对初稳性影响的实验教学过程中具有操作简便，实验验证效果清晰的特点。经过性能分析，可以得到以下几点结论：

(1)实验模型对于装卸载荷、移动载荷的模拟实验精度较高，一般可达到5%以内，可用于学生基于船模结构进行计算分析并结合实验结果进行验证；

(2)实验模型对于液体载荷自由液面的影响分析具备较好的定性分析验证条件，理论计算结果与试验验证结果存在10%左右的误差，可以满足学生进行估算并定性分析使用；

(3)实验模型精度与金加工有关，理论计算结果普遍高于实验条件，原因在于加工的精度受限，经过验证，液舱作为自由液面对稳度影响验证的保障条件，应当尽可能采用板材较薄的金属材料，且在加工过程中，通过提高精度，减小液舱间隙等手段能够进一步改进实验装置性能。

[1] 倪少玲，王少新. 船舶性能实验教学系统[J]. 实验室研究与探索, 2004,23(8): 64-66.

NI Shao-ling, WANG Shao-xin. Ship Performance Testing Teaching System [J]. Research and Exploration in Laboratory, 2004,23(8): 64-66.

[2] 张志宏，顾建农，王家楣. “流体力学”课程教学改革的实践与探索[J]. 高等理科教育, 2006(5):87-91.

ZHANG Zhi-hong, GU Jian-nong, WANG Jia-mei. Practice and Exploration of “Fluid Mechanics” course teaching reform [J]. Advanced Education of Sciences, 2006(5):87-91.

[3] 娄 敏，董文乙，陈建民. 船舶与海洋工程专业试验教学的探索[J]. 科技创新导报, 2010,24:184.

LOU Min, DONG Wen-yi, CHEN Jian-min. Explorations of the ship and ocean engineering experiment teaching [J]. Science and Technology Innovation Herald, 2010,24:184.

[4] 韩 征，王新宇. 高职教育实验教学成本探讨[J]. 实验室研究与探索, 2009,28(7): 174-176.

HAN Zheng, WANG Xin-yu. Discussion on the Experimental Teaching Cost of Vocational College Education [J]. Research and Exploration in Laboratory, 2009,28(7): 174-176.

[5] 李传英. 材料力学实验教学模式浅析[J]. 中国教育技术装备,2010,15:105-106.

LI Chuan-ying. Brief Discussion on Experimental Teaching Mode of Mechanics of Materials [J]. China Education Technology and Equipment, 2010,15:105-106.

[6] 任孔愚. 用横摇周期检验船舶稳性的实用研究[J]. 航海技术, 1996(4):1-4.

REN Kong-yu. Practical research on rolling period test of the ship stability [J]. Journal of Navigation Technology, 1996(4):1-4.

[7] 张文斌, 姚震球, 蒋志勇. 船舶稳性理论研究的方法及进展[J]. 华东船舶工业学院学报(自然科学版)，2002,16(1): 7-11.

ZHANG Wen-bin, YAO Zhen-qiu, JIANG Zhi-yong. Journal of East China Shipbuilding Institute (Natural Sciences Edition) [J], 2002,16(1): 7-11.

[8] 浦金云，刘 辉，吴向君，等. 破损进水舰船非线性横摇运动的实验研究[J]. 船舶力学, 2011,15(5): 480-489.

PU Jin-yun, LIU Hui, WU Xiang-jun,etal. Nonlinear roll motion experimental study on wreckage warship [J]. Journal of Ship Mechanics, 2011,15(5): 480-489.

[9] 阮景华. 横摇加速度与船舶安全[J]. 广西交通科技，1998,23(4): 47-48.

RUAN Jing-hua. Roll acceleration and ship safety [J]. Guangxi Science and Technology of Communication, 1998,23(4): 47-48.

[10] 马 山, 曹 宇, 马卫星. 基于能量法的船舶静水横摇试验阻尼估算方法研究[J]. 船舶力学, 2012,16(10): 1122-1131.

MA Shan, CAO Yu, MA Wei-xing. Investigation of estimation method for roll damping from calm water free decay experiment using energy method [J]. Journal of Ship Mechanics, 2012,16(10): 1122-1131.

[11] 李 浩, 陆建辉. 船舶非线性横摇运动方程的线性化研究[J]. 船舶, 2011,22(5): 1-4.

LI Hao, LU Jian-hui. On linearization of ship’s nonlinear roll motion equation [J]. Ship & Boat, 2011,22(5): 1-4.

[12] Greaves D M, Borthwick A G L, Wu G X,etal. A moving boundary finite element method for fully nonlinear wave simulations [J]. Journal of Ship Research, 1997,41(3):181-194.

[13] Lee S H, Kim J Y, Lee K J,etal. Simulation of 3D sloshing and structural response in ship’s tanks taking account of fluid-structure interaction [J]. SNAME Transactions,1995,103:321-342.

[14] 盛振邦，刘应中. 船舶原理[M]. 上海：上海交通大学出版社, 2003.

[15] 浦金云，邱金水，金 涛，等. 舰船生命力[M]. 北京：国防工业出版社, 2008.