基于神经网络—遗传算法的双层隔振系统复合振动控制

崔明月， 刘旭焱， 刘红钊， 蒋华龙

（1.南阳师范学院 物理与电子工程学院，河南 南阳 471063;2.重庆大学自动化学院，重庆 400044）

0 引言

双层隔振系统结构简单，易于实现，在噪声与振动控制领域中有着广泛应用。双层隔振装置能够显著降低机械设备振动向外界的传递，是隔离振动和结构噪声的有效措施。然而，传统被动式的隔振方式对于低频振动，尤其是双层隔振装置自身固有频率附近的振动，难以进行有效隔离［1］。主动振动控制需外界供给能量，它是利用外界能量产生控制振动所需要的力或运动［2］。这种控制效果较好，原结构改变不大，调整也方便。目前，在阻振、吸振和隔振领域，均已开展了相应的主动控制技术研究［1，3-4］。

各国学者在振动主动控制领域展开了广泛的研究，取得了显著的成果。Yagiz［5］针对7自由度汽车主动悬架的控制问题，运用反步控制策略设计了振动控制器。Rodriguez等［6］针对包含压电制动器的阻尼减振系统，基于微分平坦理论设计前馈控制律。经过各国学者的努力，振动主动控制技术在土木工程、航空航天以及车辆工程等领域均得到了广泛应用。然而，现有的振动主动控制通常只集中在削减有限模态的振动，并基于理想化的数学模型，减振效果并不十分理想。文献［7-8］用自适应控制理论进行主动控制研究，运用最小误差均方算法对系统误差通道进行在线辨识，取得了一定的控制效果。遗憾的是，该算法是以线性定常系统模型为基础。

随着神经网络理论研究的不断进展，许多基于神经网络的非线性控制策略被国内外学者先后提出，并在振动工程中得到成功应用［9-11］。遗传算法（Genetic Algorithm，GA）是一种基于自然的选择与进化机制的功能强大的随机搜索算法［12］，GA的操作不需要规划对象的先验知识，只需要计算个体的适应度值，使得该算法具有某些独到的优点，有学者曾应用于结构振动控制问题［13-14］，取得了很好效果。但是，标准遗传算法存在收敛速度慢，易于早熟等问题，影响了遗传算法控制器的实时性与准确性。

鉴于此，针对实际双层隔振系统参数时变，不易建模的特性，本文提出一种神经网络与遗传算法相结合的复合控制策略应用于双层隔振系统，构造了一种有源振动控制系统。运用三层BP神经网络作为辨识器，单纯形与标准GA相结合的改进遗传算法作为控制器，并进行了仿真分析，结果表明神经网络—遗传算法复合控制策略在双层隔振系统主动控制中的应用具有一定的可行性。

1 双层隔振装置数学模型

为了使问题简化，在此只考虑竖直方向的振动，则双层隔振系统可简化为一个两自由度的弹簧-阻尼-质量系统，如图1所示。选取隔振对象与中间块质量坐标分别为x1和x2，由牛顿定律可得双层隔振系统的振动方程［3］：

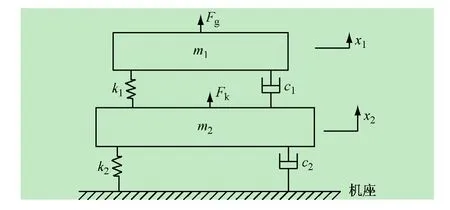
图1 双层隔振系统模型

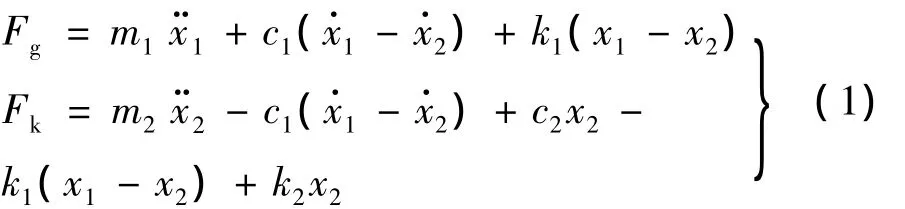
式中：m1为隔振对象的质量;m2为中间块质量;c1和c2分别为上下层隔振器阻尼系数;k1和k2分别为上下层被动隔振器的刚度系数;Fg为隔振对象工作时产生的竖直方向振动激扰力;Fk表示控制器作用力。

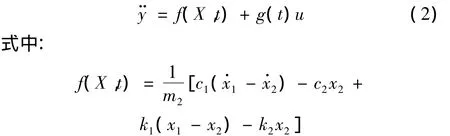
g（t）=1/m2，系统参数 m1，m2，k1，k2，c1，c2是时变的。

由于系统（2）中的f（X，t），g（t）是时变未知的，因此不能直接利用式（2）进行控制器的设计。首先要对式（2）所映射的系统输出y与控制输入u之间的关系进行辨识。

2 双层隔振系统辨识

对隔振系统辨识的目的是寻找中间质量块位移x2与竖直方向外作用力Fk的变化之间的关系，令外激扰力Fg=0进行系统辨识。双层隔振系统属于惯性系统，因此此刻输出不仅与当前刻的输入有关，也与前面时刻的输入有关，取当前时刻以及前m－1时刻的Fk作为网络的输入，如图2所示。

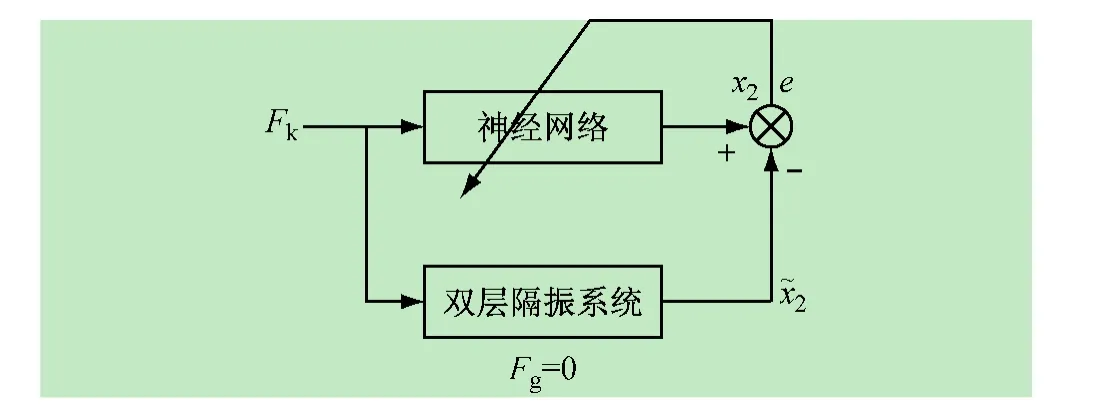
图2 隔振系统辨识器结构

2.1 神经网络权值调整算法

若输入层取为

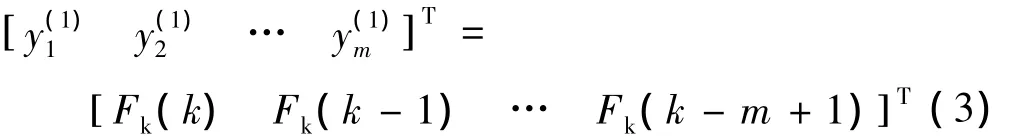
则中间层输入为

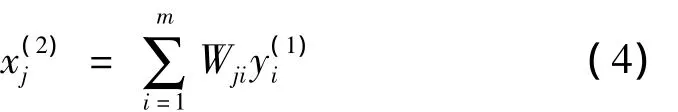
式中，Wji为输入层第i个神经元与中间层第j个神经元之间的连接权值。

式中，Wj表示输出层神经元与中间层第j个神经元之间的连接权值，激活函数取为y=x，则隔振系统中间块质量位移为

式中：x2与分别为神经网络辨识器与隔振系统中间质量块位移输出;Wji（k+1）为神经网络权值Wji的k+1时刻的更新值;μ为学习速率。

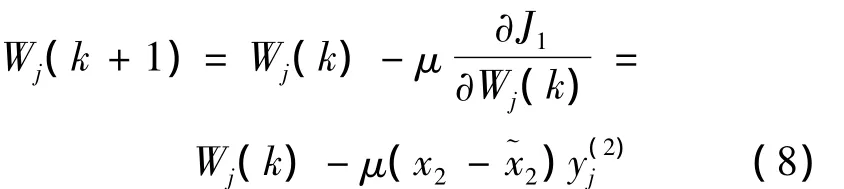
式中，Wj（k+1）为神经网络权值Wj的k+1时刻的更新值。

2.2 学习速率的自适应调整

传统的方法，学习速率μ的选择靠经验选择，如果选择太小，收敛速度慢，若选择过大，则导致振荡甚至发散，针对此问题，下面给出一种学习速率μ自适应调整算法：

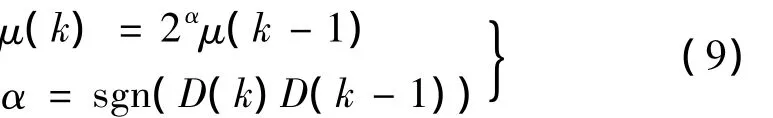
式（8）中的学习速率μ可以直接应用式（9）计算，式（7）中的μ也可以应用式（9）计算，但是此时

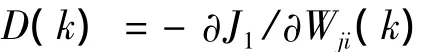
3 控制器的设计

3.1 标准遗传算法的改进

标准遗传算法局部寻优能力差，又易产生早熟，搜索后期往往在最优解附近反复进行，不能得到高精度的最优解［15］。而单纯形法是一种直接搜索方法，它具有很强的局部搜索能力，但是必须在给定合适的初始单纯形条件下，才能快速准确地收敛到初始值附近的最优解。

鉴于此，在常规遗传算法的基础上，提出了一种混合遗传算法，即在执行交叉和变异等随机性操作后，以一定的概率选择当前种群中的部分优秀个体，以这些个体为初始值，执行若干步单纯形搜索，来强化优秀个体，提高搜索效率，同时也保留了种群的个体差异性，不影响全局搜索的性能。在迭代过程中，当代价函数的适应度小于某一误差时，将取这一代种群中的最优个体作为初始值，只采用单纯形算法进行局部寻优，从而消除了遗传算法在局部搜索时的不利因素，可用更少的计算量得到问题的最优解。

3.2 神经网络控制系统的设计

系统辨识神经网络采用离线学习方式。令Fg为零，Fk采用典型的不同频率正弦信号复合，学习达到一定要求后，将权值Wji及Wj固定，在实时控制过程中不再调节。

在此，利用遗传算法在线计算施加于隔振系统中间质量块上的控制力Fk。根据第2节的研究结果，先利用BP神经网络对双层隔振结构进行辨识，再利用训练好的神经网络代替双层隔振结构进行动力分析。遗传算法—神经网络结构控制系统如图3所示。该控制系统充分发挥遗传算法控制器与神经网络辨识器各自的优点，达到了无模型实时控制的目的。

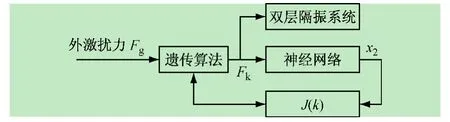
图3 神经网络控制系统

3.2.1 编码方式

要通过遗传算法寻求作用于中间质量块的最佳控制力Fk，首先就要对控制力进行编码组成染色体。因为在实际双层隔振结构中安装实施控制的执行器不太多，在此采用简单的二进制编码。

如果控制力Fk有其变化范围，用二进制字符串表示每个控制力，则控制力字符串表示值和实际控制力之间的关系如下：

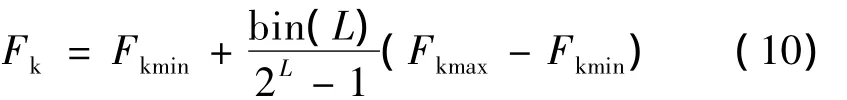
其中：bin（L）为一由L位字符串所表示的二进制整数;［Fkmin，Fkmax］为控制力Fk的变化范围。对控制力Fk进行编码，连接起来就组成了染色体。

控制目标函数取为：

3.2.2 交叉、变异概率的自适应选择

标准遗传算法中，由于交叉概率与变异概率是固定不变的，易出现过早熟现象而仅得到局部最优解。因此本文采用自适应的交叉概率Pc和变异概率Pm。Pc与Pm能够随着适应度大小进行自适应调整：

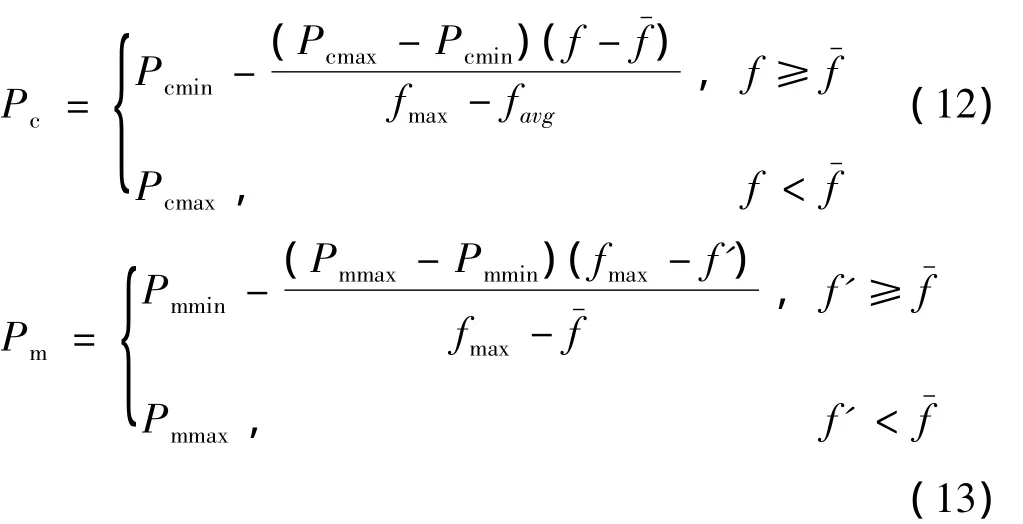
3.2.3 遗传算法控制器的工作过程

在算法的开始阶段主要利用遗传算法的全局寻优的能力，并以一定的概率对某些优秀个体进行单纯形运算，提高搜索速度，当适应度小于允许误差时，就选择该子代中的最优个体进行单纯形寻优，最后输出结果。

从第一个采样时刻k=1开始，根据外激扰力Fg计算控制力实施控制的具体流程如图4所示。

将混合遗传算法控制器计算的控制力施加于双层隔振结构，进行下一时刻（k+1时刻）的计算，重复图4所述步骤。

4 数值仿真

双层隔振系统各部分仿真参数如下：m1=105.42（kg），m2（t）=50+9sin t（kg），k1=5.7 MN/m，k2=1.90 MN/m，阻尼器的系数 c1（t）=0.1+0.05e－0.1t（N/（m·s－1）），c2=0.1（N/（m·s－1））。

4.1 双层隔振系统的特性辨识仿真

辨识系统输入信号选为

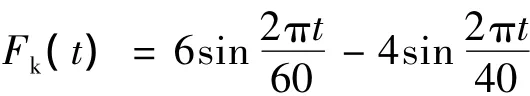
经反复训练，辨识神经网络采用16-8-1（分别表示输入层、中间层与输出层神经元的个数）型，学习因子μ（k）初始值取0.1。辨识结果如图5所示。由图5可以看出，训练后神经网络的误差能够达到预先设定的目标值，神经网络辨识器的输出较好地拟合了双层隔振结构的动态响应曲线。神经网络的输入—输出之间的关系基本上能够反映出双层隔振系统控制力与中间质量位移之间的动态变化趋势。

4.2 双层隔振系统振动控制仿真

遗传算法控制器参数选取如下：初始群体随机产生;选择策略采用适应度比例法，即选择概率按照转轮法进行调整;交叉概率Pc按式（12）进行自适应调整，采用双点交叉策略;自适应变异概率Pm按式（13）进行调整;停止准则为连续80代目标函数值不变。

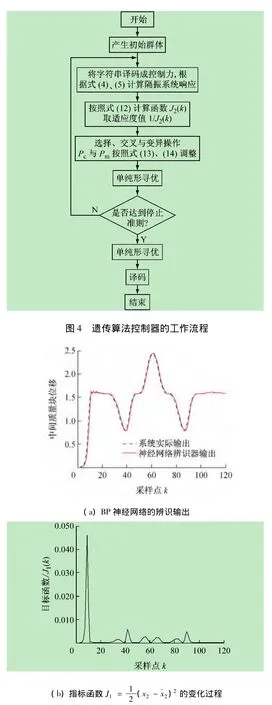
图5 系统特性辨识结果

4.2.1 持续激励下的主动控制仿真

现实中的外界激励可由不同频率的激励信号叠合而成［16］，为了考察不同频率的持续外界激励对双层隔振系统减振效果的影响，分别以频率为2、4和10 Hz，幅值为0.1 m的正弦信号作为外激励信号进行仿真，可得中间质量块m2的位移响应曲线，如图6所示。

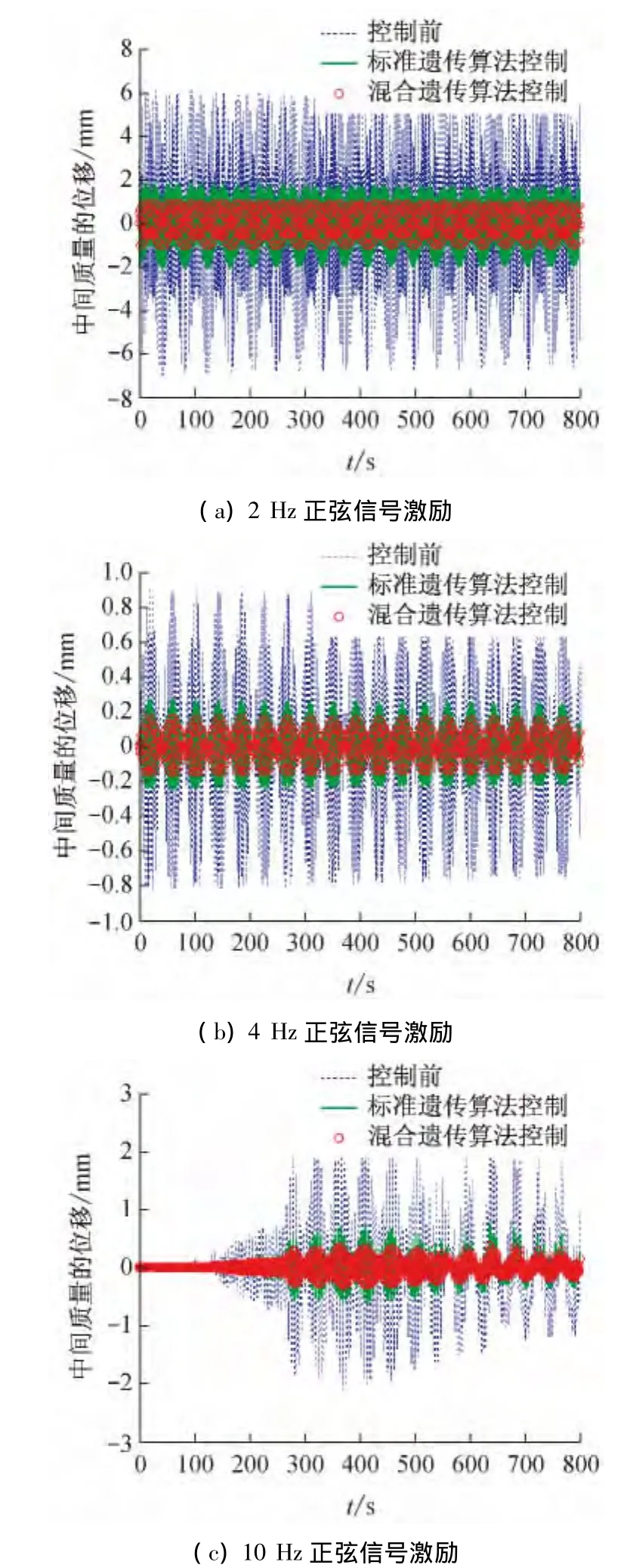
图6 中间质量块的位移响应

从图6中的中间质量块m2的振动位移响应，可以发现在外部激励信号频率分别为2、4、10 Hz的情况下，在激励频率处采用神经网络—标准遗传算法复合控制时振动位移的幅值分别是双层被动隔振时的30%、30%、50%，而采用神经网络—混合遗传算法复合控制策略时振动位移的幅值分别是双层被动隔振时的15%、18%、15%，这说明采用神经网络-混合遗传算法复合控制策略后的双层主动隔振系统具有更加良好的隔振效果。但是，激励信号的频率对隔振效果有较大的影响，随着激励信号的频率的增加，双层有源隔振系统的减震效果变差。这主要是遗传算法控制器的实时性引起的，因此寻求收敛速度更快，更精确的遗传算法可以在一定程度上解决这一问题。

需要指出的是，这种有源控制方法并未完全解决高频部分的控制问题，高频振动部分可考虑由被动隔振部分予以吸收。

4.2.2 初始扰动下的瞬态振动控制仿真

由振动力学的知识可知，现实的振动多为自由振动，即激励消失后系统所作的振动，反映的是系统关于振动的固有属性［13］。为此，需要考察瞬态响应时双层隔振系统的减振效果。在瞬态响应分析中，控制器参数保持不变，对双层隔振系统的施加一个激扰力Fg作用于上层质量块使中间质量块产生一个5 cm的初始位移，然后释放，图7是瞬间激扰力作用下运用神经网络—遗传算法复合振动控制策略的减振效果。

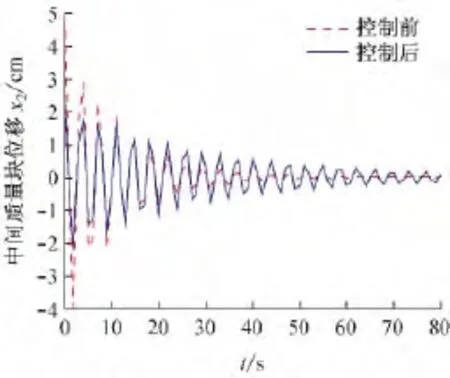
图7 瞬间激扰力作用下的减振效果

本文所提出的主动控制算法在实际应用中无论对外加的瞬间激扰力与持续激扰力的作用都具有较好的减振效果。这为该减振控制算法在工程实际中的应用提供了一种思路，即不需要建立双层隔振系统的动态模型，神经网络辨识器的学习和遗传算法在线控制可同时在线进行，实现隔振系统的无模型控制。

3 结语

为了提高系统参数时变双层隔振系统的振动控制效果，提出了将遗传算法与神经网络应用于双层隔振系统有源控制的新方法。该方法利用改进的混合遗传算法在线计算控制力，利用神经网络模拟隔振系统的动力特性，离线训练后代替隔振系统进行动力分析。仿真结果表明这种神经网络—遗传算法的复合有源振动控制策略是行之有效的。

（References）：

［1］ 杨铁军，顾仲权，刘志刚，等.双层隔振系统耦合振动主动控制实验研究［J］.振动工程学报，2003，16（2）：149-152.

YANG Tie-jun，GU Zhong-quan，LIU Zhi-gang，et al.Experimen tal Research on Active Control of Coupled Vibration for a Two-Stage Isolation System［J］.Journal of Vibration Engineering，2003，16（2）：149-152.

［2］ 顾仲权，马扣根，陈卫东.振动主动控制［M］.北京：国防工业出版社，1997.

［3］ 高宏伟，罗 军，贾建援.双层隔振系统主动控制的建模与仿真［J］.机械科学与技术，2005，24（11）：1340-1342.

GAO Hong-wei，LUO Jun，JIA Jian-yuan.Modeling and Simulation of Active Control of Two-layer Vibration Isolation System［J］.Mechanical Science and Technology，2005，24（11）：1340-1342.

［4］ 钟民军，胡世峰，史铁林等.双层混合隔振系统的CMAC和PID复合控制研究［J］.中国机械工程，2008，19（13）：1547-1551.

ZHONG Min-jun， HU Shi-feng， SHITie-lin. Studyonthe Compound Control of CMAC and PID to the Hybrid Two Stage Vibration Isolation System［J］.China Mechanical Engineering，2008，19（13）：1547-1551.

［5］ N.Yagiz，Y.Hacioglu.Backstepping control of a vehicle with active suspensions［J］.Control Engineer Practice，2008，16（12）：1457-1467.

［6］ J.M. Rodriguez-Fortun， J. Orusetc. Flatness-Based Active Vibration Control for Piezoelectric Actuators［J］.IEEE/ASME Transactions on Mechatronics，2013，18（1）：221-229.

［7］ 杨铁军，刘志刚，张文平，等.基于x-RLMS算法的自适应有源隔振技术研究［J］.内燃机学报，2001，19（1）：92-95.

YANG Tie-jun， LIU Zhi-gang， ZHANG Wen-ping， etal.Investigation in Active Vibration Isolation Based on x-RLMS Algorithm［J］.Transactions of CSICE，2001，19（1）：92-95.

［8］ 鲁民月，顾仲权，杨铁军.简化的结构振动自适应前馈控制方法研究［J］.振动与冲击，2005，24（1）：98-93.

LU Min-yue，GU Zhong-quan，YANG Tie-jun.Study on Simplified Adaptive Feedforward Control for Vibration Reduction of Structures［J］.Joural of Vibration and Shock，2005，24（1）：98-93.

［9］ 欧进萍，张利芳.模糊神经网络控制系统优化的实整数混合编码遗传算法［J］.地震工程与工程振动，2003，23（1）：11-17.

OU Jin-ping，ZHANG Li-fang.A genetic algorithm with real integer mixture encoding for optimization of fuzzy neural network control systems［J］.Earthquake Engineering and Engineering Vibration，2003，23（1）：11-17.

［10］ 孙承顺，任少云，张建武等.神经网络控制在柴油机主动隔振中的应用［J］.振动工程学报，2003，16（3）：311-315.

SUN Cheng-shun，REN Shao-yun，ZHAN Jian-wu.Application of Artificial Neural Network to Active Vibration Control of Diesel Engine［J］.Journal of Vibration Engineering，2003，16（3）：311-315.

［11］ 颜桂云，陈福全，孙炳楠.模糊神经网络在高层建筑横风向振动控制中的应用研究［J］.振动与冲击，2007，26（1）：69-76.

YAN Gui-yun， CHEN Fu-quan， SUN Bing-nan. Stduyon Application of Fuzzy Neural Network to Active Control of Across Wind Response of Tall Buildings［J］.Joural of Vibration and Shock，2007，26（1）：69-76.

［12］ 周 明，孙树栋.遗传算法原理及应用［M］.国防工业出版社，1996.

［13］ 何玉敖，郭 婷.基于遗传算法的结构主动控制［J］.振动工程学报，1999，12（2）：182-187.

HE Yu-ao，GUO Ting.Active Structural Control Based on Genetic Algorithms［J］.Journal of Vibration Engineering，1999，12（2）：182-187.

［14］ 何玉敖，郭 婷.遗传算法-神经网络结构控制系统研究［J］.振动工程学报，2001，14（2）：192-195.

HE Yu-ao，GUO Ting.Study on Structural Active Control by Genetic Algorithm-Neural Network System ［J］. JournalofVibration Engineering，2001，14（2）：192-195.

［15］ 柳建新，童孝忠，李爱勇，等.MT资料反演的一种实数编码混合遗传算法［J］.中南大学学报（自然科学版），2007，38（1）：160-163.

LIU Jian-xin，TONG Xiao-zhong，LI Jian-rong.A Real Coded Hybrid Genetic Algorithm in Magnetotellurk Sounding Data Invesion［J］.J Cent South Univ（Science and Technology），2007（1）：160-163.

［16］ 刘延柱，陈文良，陈立群.振动力学［M］.北京：高等教育出版社，1998.