一种改进的自适应中值滤波算法*

2014-02-10张涛,张欣

通信技术 2014年8期

关键词：极小值极大值中值

张涛,张欣

(贵州大学电子与信息学院,贵州贵阳550025)

一种改进的自适应中值滤波算法*

张涛,张欣

(贵州大学电子与信息学院,贵州贵阳550025)

针对传统自适应中值滤波算法的不足,文中提出了一种改进的自适应中值滤波方法,以有效的去除图像中的高密度脉冲噪声。第一,对于噪声点的检测,首先利用极大值和极小值的数量差找出可疑的噪声点,再利用邻域像素的相似性判断可疑点是否为噪声点。第二,对于滤波中值的计算,先把滤波窗口内具有相同灰度值的极值点压缩到一个,然后再计算中值。实验结果表明,该算法的滤波效果优于传统自适应中值滤波,且具有较好的稳定性。

中值滤波脉冲噪声自适应极值

0 引言

图像在传输和接收的过程中,不可避免地受到外界的干扰,如由传感器产生的热噪声、脉冲噪声,数字化过程中出现的量化噪声等,这对后期的图像处理带来严重的影响,因此有必要对其进行降噪处理。

对于含脉冲噪声的图像,由于噪声和图像内容相互独立,一般采用非线性滤波算法进行处理[1],传统的消除脉冲噪声的方法是中值滤波(SM)[2],它利用邻域中值代替当前像素值,但存在以下不足:①不能较好地保留图像边缘和纹理等细节;②窗口大小固定,滤波效果差;③对所有的像素采用统一的处理方法;④对高密度噪声的滤除效果并不理想。为此,研究者提出了许多改进的算法[3-8],如自适应中值滤波(AMF)[3],通过自动调节窗口的大小以实现滤波,但对高密度噪声的滤除效果不佳。加权中值滤波(WMF)[4],通过对窗口内不同像素赋以不同的权值以实现滤波,虽然保护了部分细节,但滤波效率也下降了。开关中值滤波(SMF)[5],通过在窗口内设置阈值来判断噪声点并以此进行滤波,但随着噪声密度的增加,算法的滤波效果逐渐变差。极值中值滤波(EMF)[6],通过在邻域内判断中心像素是否为极值来鉴别是不是噪声点,并以此进行滤波,但会带来图像的模糊问题。模糊加权中值滤波(FWMF)[7],通过模糊隶属函数对中值滤波进行加权以实现滤波,但如果模糊函数的选取不当,很难保证滤波的效果。

为此本文在研究自适应中值滤波的基础上,提出了一种新的自适应中值滤波算法,该算法在高密度噪声时,仍具有较好的滤波效果。

1 自适应中值滤波

自适应中值滤波算法可以自动调整窗口的大小,并且对不同噪声点采取不同的方法,因此在平滑非冲激噪声时可以保存部分细节,其滤波步骤如下。

对于大小为M×N的图像,设S(x,y)是其中一个像素的灰度值,(x,y)为该像素的二维坐标,且是方形滤波窗口的中心坐标,初始化窗口大小为3×3,Smax为允许的最大尺寸的窗口,Zmin为窗口中的最小灰度值,Zmax为窗口中的最大灰度值,Zmed为窗口内的中值,则自适应中值滤波的实现如下。

1)初始化窗口的尺寸W=3;如果Zmin＜Zmed＜Zmax,则转至步骤2),否则继续增大窗口W=W+2,如果W＜Smax,则重复步骤1),否则输出Zmed。

2)如果Zmin＜S(x,y)＜Zmax,则输出

S(x,y),否则输出Zmed。

从中可以看出,该算法对噪声的判断是基于最小值Zmin和最大值Zmax,如果Zmin=S(x,y),或者S(x,y)=Zmax,则判为噪声点,这对边缘或高频处的点会造成误判,从而不能很好的保存边缘和细节。另外当窗口达到最大且Zmin=Zmed或者Zmed=Zmax时,直接输出中值Zmed,而不讨论该点是否为噪声点,这样就使滤波器的去噪性能下降。并且在步骤2)中直接用Zmed代替噪声点,会造成图像的模糊。

2 改进的自适应中值算法

2.1 噪声点的检测

对于脉冲噪声,其出现极大值和极小值的概率近似相等,因此在窗口中如果极大值和极小值的数量差距很大,则可判定数量较多的极值点为非噪声点;当两者的数量大致相等时,再利用中心像素和周边像素的信息来判断其是否为噪声点。

如图1所示,在5×5的滤波窗口内,图1(a)所示的极大值为255,共有2个,极小值为140,共有1个,二者数量大致相等,都有可能是噪声点,但中心像素值与周边像素值的差值较大,可判定为是噪声点。对于图1(b),极大值为255,共有11个,极小值为0,共有1个,极大值的个数远多于极小值的个数,因此可判定极大值为非噪声点,故中心像素为非噪声点。

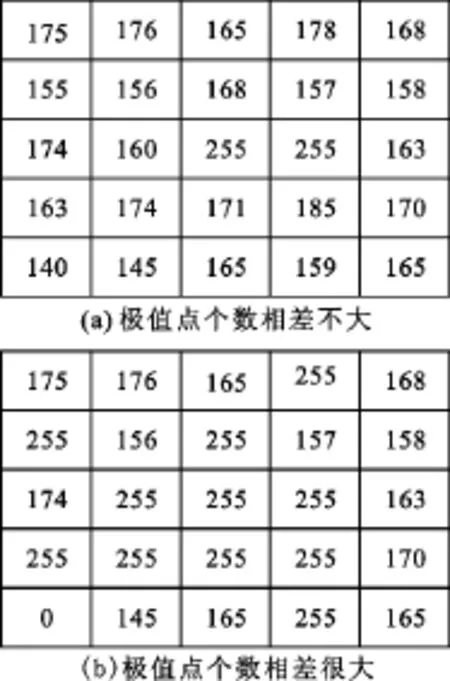
图1 图像灰度值Fig.1 Gray value of image

2.2 中值Zmed的新算法

对于传统的自适应中值滤波算法,当噪声密度较大时,获得的Zmed很有可能就是噪声点。例如对于噪声密度为80%的Lena图像,取中心点在(268,268),滤波窗口为3×3,其灰度值矩阵如图2所示。

图2 图像灰度值Fig.2 Gray value of image

则由传统算法获得的中值Zmed=255,此时的滤波失效。为此可以先删除重复的极小值和极大值,各保留一个,然后再取中值。对于上述的灰度值矩阵,经压缩后为{0,125,132,255},再求中值Zmed= 128,这样滤波器就能正常的工作,并且还可以避免噪声的传播,也减少了滤波窗口增大的次数,由此还可以提高算法的执行效率。

2.3 本文的滤波算法

1)初始化滤波窗口W=3。

2)利用新的中值算法求Zmed;如果Zmin＜Zmed＜Zmax,则转至步骤3),否则继续增大窗口W=W+2,如果W＜Smax,则重复步骤2),否则输出Zmed。

3)若S(x,y)不是极值点,则输出S(x,y),否则转至步骤4)。

4)统计窗口中极大值Zmax的个数m,极小值的个数n,若|m-n|≦T(可取为0.4×W),则转至步骤5),否则转至步骤6)。

5)若S(x,y)与周围像素的差值较小,输出S(x,y),否则输出Zmed。

6)若S(x,y)是极大值且m＞n,或者S(x,y)。

是极小值且n＞m,输出S(x,y),否则x出Zmed。

3 实验结果及分析

为了验证本文算法,用Matlab对256×256的Lena图像进行了仿真实验,最大窗口尺寸设为5×5。对于图像的滤波效果采用主观评价和客观评价两种标准。从图3可以看出当原图加入浓度为40%的噪声后(如图3(b)),经过传统自适应中值滤波器后仍有少量的残留噪声,而经本文算法滤波后图像(如图3(d))的效果基本接近原始图像图3(a)。当噪声的浓度为80%(如图3(e))时,本文算法的滤波效果(如图3(g))明显优于传统自适应中值滤波的效果(如图3(f))。所以在主观感受上本算法具有较好的滤波性能。

本文采用的客观评价标准主要有均方误差(MSE,Mean Squared Error)和信噪比(SNR,Signal -to-Noise Rate)。均方误差MSE的计算公式为:式中,为恢复后重建的图像灰度值,S为原始图像灰度值。

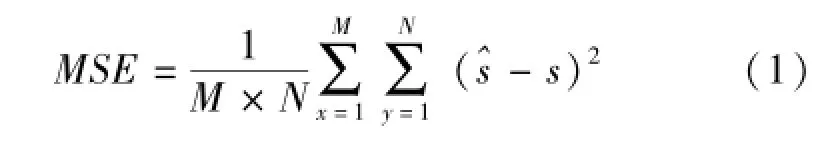
信噪比SNR的计算公式为:

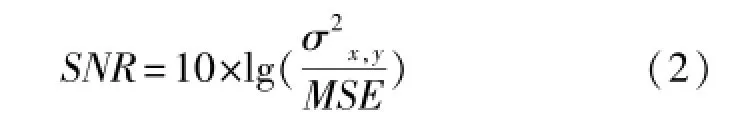
图3 各种滤波方法对加入椒盐噪声的Lena图像滤波效果比较Fig.3 Efficiency of some filters for Lena image with salt&pepper noises

从表1中可以看出在噪声浓度相同的情况下,本文算法的MSE要小于传统自适应中值滤波的MSE;本文算法的SNR要大于传统自适应中值滤波的SNR。并且随着噪声浓度的增加,传统自适应中值滤波算法的MSE和SNR变化的幅度较大,特别是在噪声浓度较大时,这种变化更加明显,而本文算法的MSE和SNR变化的幅度并不大,因此本文算法的稳定性比较好。

表1 不同水平的脉冲噪声图像通过不同去噪算法后的均方误差和信噪比Table 1 MSE and SNR of different levels of impulse noise image through different de-noising algorithm

4 结语

本文通过改进噪声点检测算法和滤波中值计算算法,提出了一种改进的自适应中值滤波算法,实验分析和仿真表明,无论是主观感受还是客观评价,该算法均优于传统自适应中值滤波算法,在高密度脉冲噪声的情况下,这种现象更明显。后续的研究中希望能够更充分利用像素之间的关联进行滤波,并且如何在有效的滤波下更好的保护图像的细节一直是图像去噪的研究重点。

[1] GONZALEZ R C,WOOD R E.Digital Image Processing [M].Second Edition.Beijing:Publishing House of Electronics Industry,2002:183-193.

[2] 董继扬,张军英.一种简单的椒盐噪声滤波算法[J].计算机工程与应用,2003,39(20):27-28.

DONG J Y,ZHANG J Y.A Simple Algorithm for Removing Salt and Pepper Noise[J].Computer Engineering and Application.2003,39(20):27-28.

[3] HWANG H,HADDAD R A.Adaptive Median Filters: New Algorithms and Results[J].IEEE Transaction on Image Processing,1995,4(04):499-502.

[4] BROWNRIGG D.The Weighted Median Filter[J].Communication Association Computer Machine,1984,27 (08):807-818.

[5] SUN T,NEUVO Y.Detail-preserving Median Based Filters in Image Processing[J].Patten Recognition Letters, 1994,15(04):341-347.

[6] 胡旺,李志蜀,黄奇.基于双窗口和极值压缩的自适应中值滤波[J].中国图像图形学报,2007,12(01):43-50.

HU W,LI Z S,HUANG Q.An Adaptive Median Filter Based on The Double Windows and Extremum-Compressing[J].Journal of Image and Graphics,2007,12 (01):43-50.

[7] Eng How-lung,Ma Kai-kuang.Noise Adaptive Soft-Switching Median Filter[J].IEEE Transactions on Image Processing,2001,10(02):242-251.

[8] 尹剑仑,卫武迪.一种改进的自适应中值滤波算法研究[J].通信技术,2009,42(11):241-243.

YIN J L,WEI W D.The Research of The Ameliorated A-daptive Median Filter Algorithm[J].Communications Technology,2009,42(11):241-243.

ZHANG Tao(1990-),male,graduate student,majoring in image processing.

张欣(1976—),男,博士,副教授,硕士生导师,研究方向为下一代无线通信及应用、无线传感器网络。

ZHANG Xin(1976-),male,Ph.D.,associate professor, M.Sci.tutor,mainly working at the next generation of wireless communications and applications,wireless sensor networks.

An Improved Adaptive Median Filter Algorithm

ZHANG Tao1,ZHANG Xin2*
(School of Electronics and Information,Guizhou University,Guiyang Guizhou 550025,China)

To overcome the drawbacks of the traditional adaptive median filter,an improved adaptive median filter is proposed to effectively remove the high density impulse noise of the image in this paper.Firstly, detect noise points.Different point values between the maximum and minimum points are used to identify suspicious noises.Then,the similarity of neighborhood pixels is used to judge these suspicious points whether they are noise points or not.Secondly,calculate the filtering median.Extreme points that have the same gray value in the filter window are compressed to only one.Finally,calculate the median values.The experimental result shows that this algorithm is better than traditional adaptive median filter to remove the noise and has a good stability.

median filter;impulse noise;adaptive;extreme value

TP751.1

1002-0802(2014)08-0873-04

10.3969/j.issn.1002-0802.2014.08.007