切换控制在动力定位系统中运用的研究与进展

金 鑫， 王 磊， 徐胜文

(上海交通大学 海洋工程国家重点实验室, 上海 200240)

0 引 言

切换控制作为控制理论中的一种方法，在计算机学科、控制工程以及应用数学等领域都有着广泛的运用[1-3]。一套完整的切换控制系统是一个动态系统，该系统可以用一组连续或离散的动态变量以及基于逻辑的状态切换来描述。这些动态变量是基于不同的模式的，而这些不同的模式也就是通常所说的触发系统进行状态切换的“事件”[4]。

动力定位系统( dynamic positioning system) 是一套闭环的控制系统，以不同的控制方程作为自动定位和导航的指导，通过桨、舵和推进器的配合使用，保持船舶或者平台的位置和姿态。文献[5]中关于动力定位系统早期发展的描述可以在文献[6]中找到，其控制系统的发展同样经历了由简入繁、不断深入的过程。20世纪70年代诞生的第一艘动力定位船舶只考虑水平面的三种运动模式(横荡，纵荡和首摇)，采用的是单输入单输出的PID控制，配合低通滤波和带阻滤波器[7]。到了80年代，更为先进的基于多变量优化的控制策略以及卡尔曼滤波器理论被提出。这套控制策略被不断地优化和发展，其中结合了基于卡尔曼滤波理论的波浪滤波技术的观测器的提出可以视作船舶控制系统领域的一个突破，并且对许多其他的船舶控制的应用也有促进[8]。

随着动力定位应用领域的拓展，锚泊辅助动力定位[9]、冰区动力定位[10]以及5自由度运动控制[11]等课题渐渐成为研究热点。这三种应用背景虽然各有区别，但是在动力定位的控制系统设计上，都需要面对一个共同的问题——多工作模式切换。锚泊辅助动力定位需要在纯动力定位、锚泊辅助以及纯锚泊之间切换，冰区动力定位则需要在有冰载工况和无冰载工况间切换，5自由度运动控制则需要考虑何时开启和关闭5自由度控制功能。显然，这些切换都应该由控制系统自身根据外部载荷和环境条件的变化，做出相应的判断，并且平滑、高效地切换到相应的工作模式。国内外在相关理论和应用角度都开展了研究，本文将对相关理论和研究进行综合，提出一点自己的见解，以期对后续研究工作有一定的指导作用。

1 切换控制相关理论

切换控制在航空、控制工程以及计算机学科等领域都有成熟的运用，系统的稳定性一直都是其中的一个重点。文献[7]中监督切换控制理论的提出[12-14]则使控制的稳定性得到了较大的改善，也是动力定位领域所采用的切换控制理论的基础，因而本部分将对此进行简要介绍。

图1展示了切换控制的基本结构。图中：u表示控制信号；w表示外界干扰和观测噪声；y表示控制输出；虚线框所标示部分即为切换控制的核心部分。

图1 切换控制结构图

假设我们需要在控制器组C中进行控制器切换，变量表示为q∈Q，Q表示参数集合，其为有限、无限但可数甚至于不可数均可，所有的zq均具有相同的维度，则切换控制可以表示为：

(1)

在控制器组中的切换可以使用以下的多控制器来表示：

(2)

其中，信号σ:[0, ∞)→Q称为切换信号，能决定每一时刻系统所采用的控制器。

图1中最为重要的是产生切换信号的逻辑，这种逻辑称为监督器，它的作用是控制测试到的信号(在此处就是u和y)并且决定每一时刻接入控制回路中的控制器。此处所提出的切换控制和传统的基于连续调谐的主动控制的区别在于监督器中采用了控制学习过程的逻辑。实际上，传统的主动控制可以看作是一种特殊的切换控制，其切换信号σ通过如下所示的常微分方程产生：

(3)

2 动力定位系统的相关理论

2.1 坐标系定义

图2 动力定位坐标系定义图

在动力定位系统中，运动通常采用如图2所示的三组坐标系进行表示。

(1) 地球固定坐标系(XEYEZE)。该坐标系用于测量船舶相对于定义原点的位置和首向角，每个位置参考系统(例如全球定位系统(GPS)、水声参考系统等)的局部坐标系都是通过一个共同的地球固定坐标系平移得到的。

(2) 随船坐标系(XYZ)。该坐标系是固定于船上并且随船一起运动的，坐标原点通常选取在船舶的重心位置。

(3) 参考平行坐标系(XRYRZR)。该坐标系也可称为水动力坐标系，通常是沿着船舶航行轨迹进行平面运动，不随船舶摇动。在动力定位系统中，该坐标系固定于定位的目标点，与地球坐标系的夹角即为动力定位的目标首向角。

地球固定坐标系中船舶的位置和首向角与随船坐标系中船舶的速度可以通过转换矩阵[15]J(η)∈R6×6求得，其关系式为

(4)

如果只考虑3自由度的运动，则速度关系式可简化为

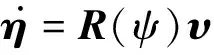
(5)

(6)

2.2 非线性低频运动

船舶6自由度低频运动模型在文献[15]中有详细讲述，其运动方程可以表示为

τenv+τmoor+τc

(7)

其中:M∈R6×6为船舶质量矩阵，包括附加质量；CRB(ν)∈R6×6和CA(ν)∈R6×6分别为船舶刚体和附加质量的科氏力和向心力作用矩阵；D(νr)∈R6为船舶阻尼向量，是关于船舶与流的相对速度νr∈R6的函数；G(η)∈R6为广义回复力向量，由浮力和重力产生；τenv∈R6为风力和二阶波浪力向量；τmoor∈R6为系泊力向量，本文将有详细描述；τc∈R6为控制向量，包括推进系统产生的推力和力矩。

2.3 线性波频运动

线性波频运动方程可以表示为：

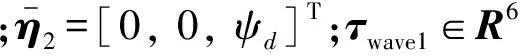
2.4 锚泊载荷

锚泊系统由一组通过转塔连接或者直接连接到船舶上的锚泊线组成。锚泊线的运动形式通常包括大幅低频运动、中幅波频运动和小幅特高频涡激振动。在考虑锚泊影响的控制系统设计中，通常将锚泊的影响在低频运动模型中进行考虑。水平分布的锚泊模型可以用以下公式表示：

τmoor=-J-1(η2)gmo(η)-dmo(νr)

(10)

其中，dmo和gmo∈R6分别为由于锚泊系统存在而产生的附加阻尼向量和地球固定坐标系下的回复力向量。

2.5 冰区载荷

航行于冰区的船舶，会承受的来自浮冰的冲击载荷，相关理论研究早有开展[17-19]，此处只讲述破冰机理[20]。

船舶与冰床接触，首先会发生挤压，随着接触面积的增加，挤压力持续增加。当挤压力增加到一定程度，垂向分量引起的弯矩会使冰床局部发生弯曲破断，形成浮冰。随着船舶的前进，浮冰沿着船体移动，并且在新产生的浮冰的推挤下，沿着船体下沉，直到与船体不再发生接触。

3 切换控制在动力定位中的运用

3.1 国外相关领域

国外相关领域的应用研究主要采用的控制思想还是前文所提到的监督切换控制，应用领域多为锚泊辅助动力定位，在冰区动力定位领域的应用也有研究。

Nguyen[21]研究了在平静海况以及恶劣海况下，切换控制在动力定位模式和锚泊辅助动力定位模式之间切换的适用性，并且开展了数值仿真模拟和模型试验，均表明切换控制对动力定位系统的整体稳定性没有负面影响，同时多控制模式比单一控制模式具有更高的工作效率。

Nguyen等[22]研究了恶劣海况中，不进行波频滤波并且加入速度反馈控制器后的观测器与进行波频滤波并且加入PID控制器的传统观测器间的区别，并且将新的观测器引入到切换控制的设计中，进行了数值模拟和模型试验，证明切换控制能达到拓宽动力定位系统作业窗口的效果。其中，该切换控制进行切换的依据是采用监督控制追踪波浪峰值频率是否变化。

Nguyen等[23]对动力定位中切换控制的特点及基本结构进行了介绍，以穿梭油轮为例，设计了适用于固定环境条件下，可变航速及工作模式的切换控制系统，并且进行了模型试验，验证了监督切换控制器在动力定位、低速航行和变化工作状况之间进行切换的有效性。

Nguyen等[24]拓宽了切换控制进行切换的标准，将平均扰动载荷以及波浪峰值频率共同作为切换的标准，并且将定位点自动寻优[25]方法引入到控制器的设计中，开展了数值模拟和模型试验，表明切换控制在锚泊辅助动力定位中相对于单状态控制器具有更好的控制效果。

Skogvold[26]采用环境最有控制策略[27]，引入冰区观测器和信号无抖动切换方法，以支持船为研究对象，研究了切换控制在冰区的适用性，并且使用挪威科技大学的Marine Cybernetics Simulator模拟程序对所设计的整个系统进行了模拟。

3.2 国内相关领域

国内在相关领域的研究基本处于仿真模拟阶段，相关的模型验证试验未见开展。

郭娟[28]设计了满足不同海况条件下工作任务要求的系统观测器和控制器，引入开关逻辑算法设计混合控制器，建立可以在多种海况条件下自动切换控制算法和模型的动力定位混合控制系统，并通过计算机仿真验证所设计的控制器的控制效果。

陈豪[29]将非线性的控制对象模型拆解为4个连续的线性部分，并用离散的模糊切换规则将其融合为一个混杂系统，设计了针对多海况条件下的动力定位多PID切换控制系统，并用计算机软件对此控制系统进行仿真实验。

4 结 语

本文对切换控制以及动力定位的基本原理进行了简要介绍，并且对国内外关于切换控制在动力定位领域的应用研究及进展进行了总结和概括。通过总结可以发现：

(1) 国内目前在该领域的研究主要以仿真为主，未见有相关验证试验开展，后期可结合验证试验，对切换控制的效果和特点进行进一步的研究；

(2) 国外在该领域的研究以试验和仿真相结合，在锚泊辅助动力定位中的应用以开展较多研究，在实验条件下证明了切换控制系统相较于单模式控制系统具有更好的控制效果；

(3) 目前切换控制在冰区动力定位中的应用逐渐成为热点。现有的冰区切换控制所采用的策略还是基于环境最有控制策略，专用的冰区控制策略有待开发。

[1] Brockett R W. Hybrid models for motion control systems[M]. Cambridge: Springer,1993: 29-53.

[2] Hespanha J P. Stochastic hybrid systems: Application to communication networks[M]. Cambridge: Springer,2004: 387-401.

[3] Mestl T, Plahte E, Omholt S W. A mathematical framework for describing and analysing gene regulatory networks[J]. Journal of Theoretical Biology,1995, 176(2): 291-300.

[4] Shorten R, Wirth F, Mason O,etal. Stability criteria for switched and hybrid systems[J]. SIAM Review,2007, 49(4): 545-592.

[5] Sørensen A J, Sagatun S I, Fossen T I. Design of a dynamic positioning system using model-based control[J]. Control Engineering Practice,1996, 4(3): 359-368.

[7] Sørensen A J. A survey of dynamic positioning control systems[J]. Annual Reviews in Control,2011, 35(1): 123-136.

[8] Fossen T I, Perez T. Kalman filtering for positioning and heading control of ships and offshore rigs[J]. Control Systems,2009, 29(6): 32-46.

[9] Sorensen A, Strand J P, Fossen T I. Thruster assisted position mooring system for turret-anchored fpsos[C]// Proceedings of the 1999 IEEE International Conference on Control Applications,IEEE,1999: 1110-1117.

[10] Zhou L. Numerical and Experimental Investigation of Station-keeping in Level Ice[D]. Trondheim: CeSOS, NTNU,2012.

[11] Xu S, Wang X, Wang L,etal. Dynamic Positioning With Roll-Pitch Motion Control for a Semi-submersible[C]// The Twenty-third International Offshore and Polar Engineering Conference,International Society of Offshore and Polar Engineers. Alaska, USA,2013:973-975.

[12] Hespanha J P. Tutorial on supervisory control[C]// Lecture Notes for the workshop Control using Logic and Switching for the 40th Conference on Decision and Control, the 40th Conference on Decision and Control. Orlando, Florida, USA, 2001:3-5.

[13] Hespanha J P, Morse A S. Switching between stabilizing controllers[J]. Automatica,2002, 38(11): 1905-1917.

[14] Hespanha J P, Liberzon D, Morse A S. Hysteresis-based switching algorithms for supervisory control of uncertain systems[J]. Automatica,2003, 39(2): 263-272.

[15] Fossen T I. Handbook of marine craft hydrodynamics and motion control[M]. United Kingdom: John Wiley & Sons,2011: 151-153.

[16] Triantafyllou M S. Cable mechanics for moored floating systems[C]// BOSS '94, 7th Intl Conf on the Behaviour of Offshore Structures, Massachusetts, USA,Pergamon,1994: 57-79.

[17] Enkvist E. On the ice resistance encountered by ships operating in the continuous mode of icebreaking[M]. Finland: Swedish Academy of Engineering Sciences,1972: 76-80.

[18] Lewis J W, DE BORD F W, Bulat V A. Resistance and propulsion of ice-worthy ships[J]. Transactions-Society of Naval Architects and Marine Engineers,1982, 90: 249-276.

[19] Lindqvist G. A straightforward method for calculation of ice resistance of ships[C]// POAC 89, 10th Intl Conference, Port and Ocean Engineering under Arctic Conditions, Luleaa, Sweden,1989: 722-736.

[20] Su B, Riska K, Moan T. A numerical method for the prediction of ship performance in level ice[J]. Cold Regions Science and Technology,2010, 60(3): 177-188.

[21] Nguyen T D. Design of hybrid marine control systems for dynamic positioning[D]. Singapore National University of Singapore (NUS) Department of Civil Engineering 2006.

[22] Nguyen T D, Sørensen A J, Tong Quek S. Design of hybrid controller for dynamic positioning from calm to extreme sea conditions[J]. Automatica,2007, 43(5): 768-785.

[23] Nguyen T D, Sorensen A J, Quek S T. Multi-operational controller structure for station keeping and transit operations of marine vessels[J]. Control Systems Technology, IEEE Transactions on,2008, 16(3): 491-498.

[24] Nguyen D T, Sørensen A J. Switching control for thruster-assisted position mooring[J]. Control Engineering Practice,2009, 17(9): 985-994.

[25] Nguyen D T, Sorensen A J. Setpoint chasing for thruster-assisted position mooring[J]. IEEE Journal of Oceanic Engineering,2009, 34(4): 548-558.

[26] Skogvold M. Supervisory-switched Control for Dynamic Positioning Systems in Arctic Areas[D]. Trondheim Norway: Norwegian University of Science and Technology (NTNU) Department of Marine Technology,2010.

[27] Fossen T, Strand J P. Nonlinear passive weather optimal positioning control (WOPC) system for ships and rigs: experimental results[J]. Automatica,2001, 37(5): 701-715.

[28] 郭 娟. 不同海况条件下船舶动力定位混合控制系统设计[D]. 上海: 上海交通大学 船舶海洋与建筑工程学院,2012.

[29] 陈豪. 动力定位系统多 PID 切换控制研究[D]. 大连: 大连海事大学 轮机工程,2013.