无底柱分段崩落法崩矿步距的优化

王云鹏，余健

（中南大学 资源与安全工程学院，湖南 长沙，410083）

无底柱分段崩落法崩矿步距的优化

王云鹏，余健

（中南大学 资源与安全工程学院，湖南 长沙，410083）

基于分段高度、进路间距和崩矿步距的不同组合，对放矿损失贫化指标具有重要影响，研究结构参数优化的方法，在利用端部放矿理论贫化损失指标的计算公式确定崩矿步距的基础上，建立单位工业储量盈利最大化和单位精矿盈利最大化为目标函数的数学模型。研究结果表明：该方法改变了传统的仅考虑贫化损失指标最佳确定结构参数的方法，开辟了从保障矿床开采整体经济效益最大化确定结构参数的新途径。

崩矿步距；放矿；矿石贫化损失率；经济效益

无底柱分段崩落法是一种安全、高效、机械化程度高的采矿方法[1]。其典型方案最早在瑞典kiruma铁矿山使用，由于其显著的优点，在世界金属矿山中得到了迅速推广，特别是铁矿山的应用更为广泛[2]。由于这种采矿方法在岩石覆盖条件下放矿，矿石的贫化损失问题严重[3−4]，降低贫化损失是矿山企业追求的目标。为此，国内外采矿专家学者和生产矿山做了大量的研究工作，总结归纳出了一些典型的放矿理论[5]。由较经典的椭球体放矿理论可知：无底柱分段崩落法的贫化损失是由分段高度、进路间距及崩矿步距决定的。在矿山的实际生产中，分段高度及进路间距的确定往往受到矿山地质、采矿设备等诸多条件的制约，不易调整，而崩矿步距是灵活可变的，且存在一个最优值[6]。传统方法一般采用“回贫差”作为目标函数来确定崩矿步距，即矿石的回收率减贫化率的最大值为最优[7]。但采用“回贫差”来确定崩矿步距只能获得较好的放矿效果，其经济效益并不一定是最佳的，因为矿山的盈利还受采矿成本、选矿成本、矿石价格等诸多因素的影响，企业以最终盈利为目的，因此，无法从根本上实现崩矿步距的优化。如何利用有限的资源来获得最高的利润才是问题的关键。建立最终盈利与影响因素之间的数学模型，然后由盈利的最大值来确定崩矿步距才是解决优化问题的重要途径。本文作者拟建立以矿石价格、采矿成本、围岩品位等主要因素为参数的企业经济效益关于崩矿步距的函数关系。不同时期，任一参数的改变必然导致函数关系的改变。因此，由经济效益最佳确定的最优崩矿步距是随着市场行情和矿脉延伸不断变化的。针对某一特定时期特定矿块、矿石价格、采矿成本、围岩品位等都是固定的，经济效益由贫化损失率即崩矿步距决定，可以绘出此时的函数曲线并根据曲线确定盈利的最大值点及此时的最佳崩矿步距。

1 放矿理论的研究

1.1 放出体的数学模型

无底柱分段崩落法是在端部约束的情况下进行放矿的，放矿椭球体是一个被切割的放出椭球体缺。但是，当放矿高度超过端部后放出体的发育就失去了约束，这时的放矿条件与底部放矿时的情况近似，因此，超过端部约束之上的放出椭球体部分可近似地作为普通椭球体来处理，而且超过约束顶部的高度越多，用这种处理方式误差越小。

混入矿石中造成出矿贫化的岩石主要来自3个方向，即放出体的正面、顶部和侧面（其他方向可化为这3个方向的组合）。设每次崩矿后崩下的矿石堆体积为Vb，放出体的体积为Vd，正面废石混入的体积为V1，顶部废石混入的体积为V2，侧面废石混入的体积为V3。

式中：S为崩矿时炮孔控制的面积；L为崩矿步距；α为挤压条件下爆破后的松散系数。

大量的物理模拟实验表明：端部放矿时放出体形状为一前倾的扁椭球缺，见图1。为了提高计算的准确性，假定其下部顶点在巷道高度的1/3处，用雅可比变换法可以求出扁椭球缺的体积Vd计算式[8]：

式中：a2为放矿椭球体长轴，m；b2为垂直进路方向放矿椭球体短轴，m；c2为进路方向放矿椭球体短轴，m；θ为流轴与端壁夹角；

同理，放矿过程中放出体正面废石混入体的的体积V1为

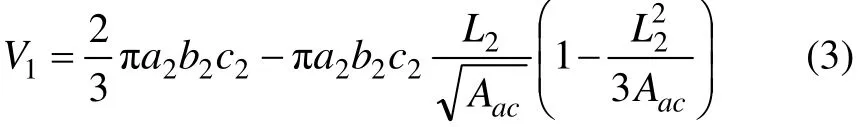
当放出椭球体的高度为h1时，纯矿石已放完，若再继续放矿，就会形成高为h2的放出椭球体，此时，矿岩接触面上部就会有（h2−h1）椭圆截锥体积V2的废石混入矿石中，此后，如果放矿继续进行，混入废石量还会不断增加。利用图2所示的关系可得出废石体积V2。

图1 正面废石混入的情况Fig. 1 Condition of positive waste rock mixed

图2 顶部废石混入的情况Fig. 2 Condition of top waste rock mixed

式中：h1为未贫化时放出椭球体高度，m；h2为最终放出椭球体高度，m；

放出体垂直进路的剖面，在这个剖面上放出体截面是一个完整的椭圆，当放出体侧面超越矿废接触面，就会造成侧面废石混入。图3所示为侧边矿岩接触面岩石混入贫化情况，由图3可知：由于放矿端壁的存在，侧面废石的混入体积等于侧边接触面所截取的放出椭球体体积的一半。进行这样的处理虽然存在一定误差，但误差很小。事实上，造成这种误差的原因是由于放出体前倾造成的，而这种前倾角度很小（仅3°～5°），因此，进行这样的处理在工程范围内是可接受的。

图3 侧边矿岩接触面岩石混入贫化情况Fig. 3 Condition of side waste rock mixed

可用式（5）计算体积V3：

式中：a1为纯矿石放矿椭球体长轴，m；b1为垂直进路方向纯矿石放矿椭球体短轴，m；c1为进路方向纯矿石放矿椭球体短轴，m。

1.2 矿石贫化率的计算

贫化是由正面、顶部和侧面的废石混入造成的，若Vd表示实际放出矿石的体积，废石混入体积为Vf，用P表示废石混入造成的体积贫化率，则有即

生产实际中围岩中经常是有一定品位的，设纯矿石的品位为C、围岩品位为Cy，令，式（6）可推演为

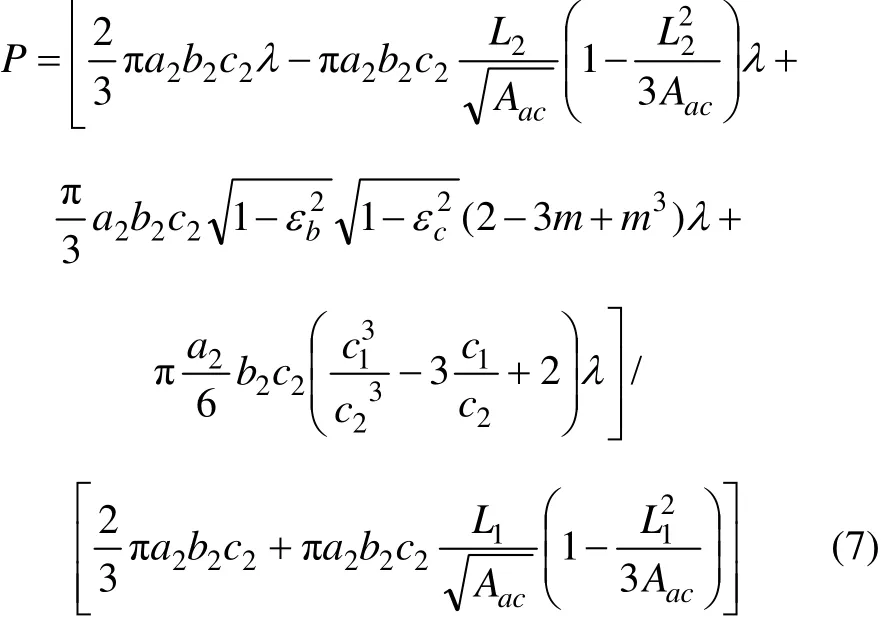
1.3 矿石回收率的计算

每次爆破崩下的矿石体积为Vb，实际放出的纯矿石体积为Vs，用H表示矿石贫化率，则有即

生产实际中围岩中经常是有一定品位的，设纯矿石的品位为C、围岩品位为Cy，令式（8）可推演为

式（7）和式（9）分别给出了3个方向岩石混入情况下贫化率和回收率的计算方法，任何岩石混入情况都可由该计算式简化而得，因而该式是无底柱分段崩落采矿贫化率和回收率的通用计算式。

2 以最佳经济效益确定崩矿步距

衡量矿山企业经济效益的标准是单位工业储量盈利，工业储量盈利是一座矿山所圈定的工业储量矿石开采销售所获得的最终盈利额，每吨矿石的盈利额即单位工业储量盈利[9]。除矿石的开采成本和矿石卖价外，单位工业储量盈利主要是受矿石的回收率和废石的混入率影响。废石的混入率是由矿石的贫化率决定的，从而矿石的贫化率和回收率是崩矿步距的函数。因此，可以建立单位工业储量盈利关于崩矿步距的函数，不同的崩矿步距会有与之相应的盈利额。当控制在某一崩矿步距下矿山的单位工业储量盈利最大，即获得最佳的经济效益，此时的崩矿步距即最优崩矿步距。

假设单位工业储量为a，崩矿步距为L，建立a关于L的函数表达式。

若矿山企业以开采出的矿石为最终产品，单位工业储量盈利额可用下式表示：

式中：m为工业储量，t；H为矿石回采率，%；Pf为废石混入率，%；Mk为采出矿石卖价，元/t；Fc为采矿成本，元/t。

式中：P为矿石贫化率，%；C为矿石工业品位，%；Cy为围岩品位，%；Ce为采出矿石品位，%。

矿石卖价取决于采出矿石品位Ce，可近似视为一次函数关系，即Mk=kCe，其中Ce=C（1−P）。

将式（7），（9）和（11）代入式（10），依然用贫化损失率代替崩矿步距，故单位工业储量盈利为

求解得出L，即为以矿石为最终产品按单位工业储量盈利最大化确定的最优崩矿步距。

若矿山企业以精矿为最终产品时，单位工业储量盈利额可用下式表示：

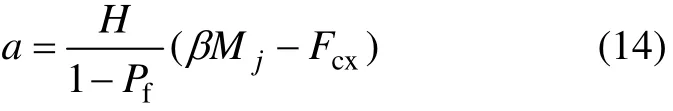
式中：β为精矿产出率，Mj为精矿卖价，元/t；Fcx为1 t矿石的采选费用，，元/t；f1为采场放矿前已付出的费用每吨储量平均摊销额，元/t；f2为采场放矿及放出以后的费用每吨采出矿石的摊销额（包括选矿费用），元/t；Hx为选矿金属回收率，%；Cj为精矿品位，%；

式中：Cc为采出矿石品位，%；Cw为尾矿品位，%；mj为精矿量，t；mc为采出矿石量。

将式（7）、式（9）、式（15）代入式（14）中，依然用贫化损失率代替崩矿步距，故单位工业储量盈利为

将式（16）对崩矿步距L求导数，并令其等于0，得

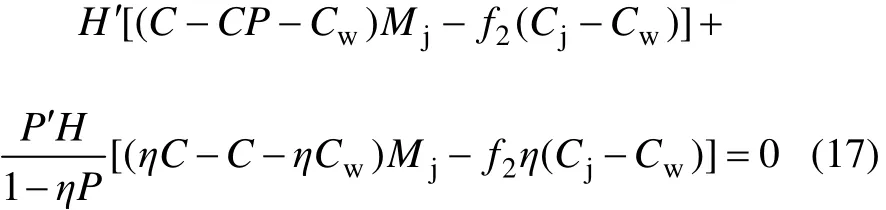
求解得出L，即为以精矿为最终产品按单位工业储量盈利最大化确定的最优崩矿步距。

式（13）和式（17）是适用于无底柱分段崩落法的通用式，根据这2个计算式解出的崩矿步距是使目标函数为极值时的崩矿步距。但是，是使目标函数为最大值或是为最小值的崩矿步距还要进行进一步分析。首先要分析计算的结果，若上式的解为负值，则显然与事实不符，可舍弃（因为崩矿步距不可能为负）；对于取正值的多个解，可以作出从小于最小值到大于最大值的数值区间，然后得出各目标函数在该区间内变化曲线（用Matlab[10]软件很容易做到），就可得出函数在该区间的变化规律，由此确定目标函数取得最大值的崩矿步距就是最优崩矿步距。

3 大红山铁矿最优崩矿步距的确定

大红山铁矿的缓倾斜厚大矿体，采用高分段大间距无底柱分段崩落法开采，目前的分段高度为20 m，进路间距20 m[11]，现利用单位工业储量盈利来确定其最优崩矿步距。

3.1 以矿石为产品确定最优崩矿步距

放出体高度为45 m，a2=22.5 m，b2=6.6 m，c2=6.8 m，θ=45°，a1=20 m，b1=6.1 m，c1=5.95 m，α=1.3，k=700，Cj=63%，C=47%，Cy=17%，Cw=15%，Fc=70元/t，Mj=650元/t，f1=30元/t，f2=65元/t。

代入式（7）和式（9）可得贫化率和回收率分别为：

将式（18）和式（19）代入式（13）即可得出a关于L的函数表达式，用Matlab软件显示函数图形，如图4所示。

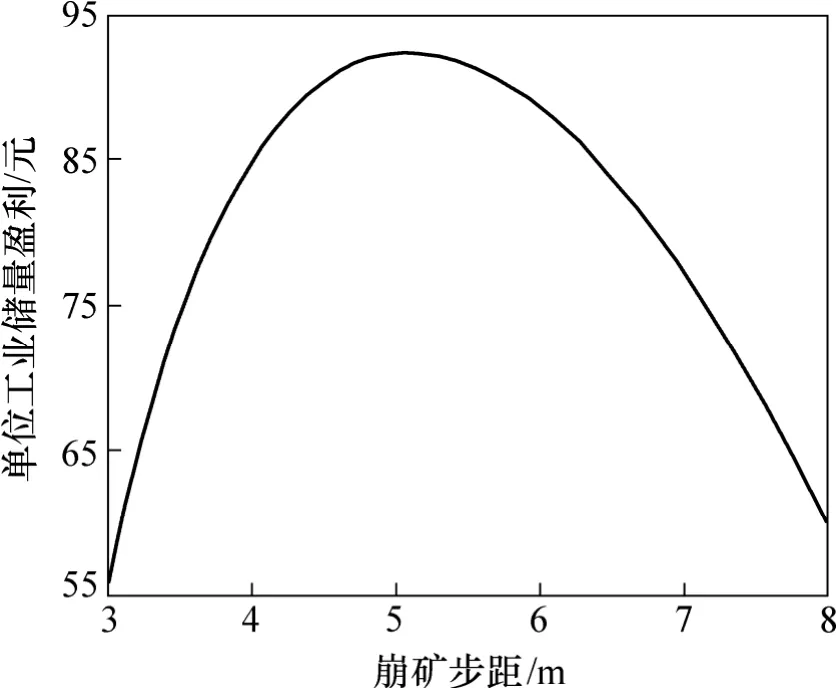
图4 a关于L的函数表达式图形Fig. 4 Curve of function a（L）

求得当L=5.10 m时，a为最大值，a的导数为0，即最优崩矿步距为5.10 m。

3.2 以精矿为最终产品确定最优崩矿步距

将参数及式（18）和式（19）代入式（9）即可得出a关于L的函数表达式，用Matlab软件显示函数图形，如图5所示。

图5 a关于L的函数表达式图形Fig. 5 Curve of function a（L）

求得当L=5.49 m时，a为最大值，a的导数为0，即最优崩矿步距为5.49 m。

3.3 最优崩矿步距的验证

前面的只是理论分析得出的最优崩矿步距，但是，生产实际中究竟使用哪种崩矿步距，还得由现场工业试验确定。现对国内外一些无底柱分段崩落法矿山，实际使用的崩矿步距与分段高度的关系进行研究来验证所求的崩矿步距是否在允许范围内。

表1所示为瑞典基律纳铁矿不同时期的崩矿步距与分段高度的比例关系，表2所示为国内一些无底柱分段崩落法矿山的崩矿步距与分段高度的比例关系。从基律纳铁矿和国内一些无底柱分段崩落采矿法矿山的崩矿步距与分段高度的比例关系可看出：一是国内外无底柱分段崩落法的矿山，使用的崩矿步距与分段高度的比值范围为0.107～0.300，平均值为0.232；二是随着分段高度的增加，其比值有降低的趋势。

表1 基律纳铁矿崩矿步距与分段高度比值的变化情况Table 1 Relationship between breaking interval and sublevel height of Kiruna iron mine

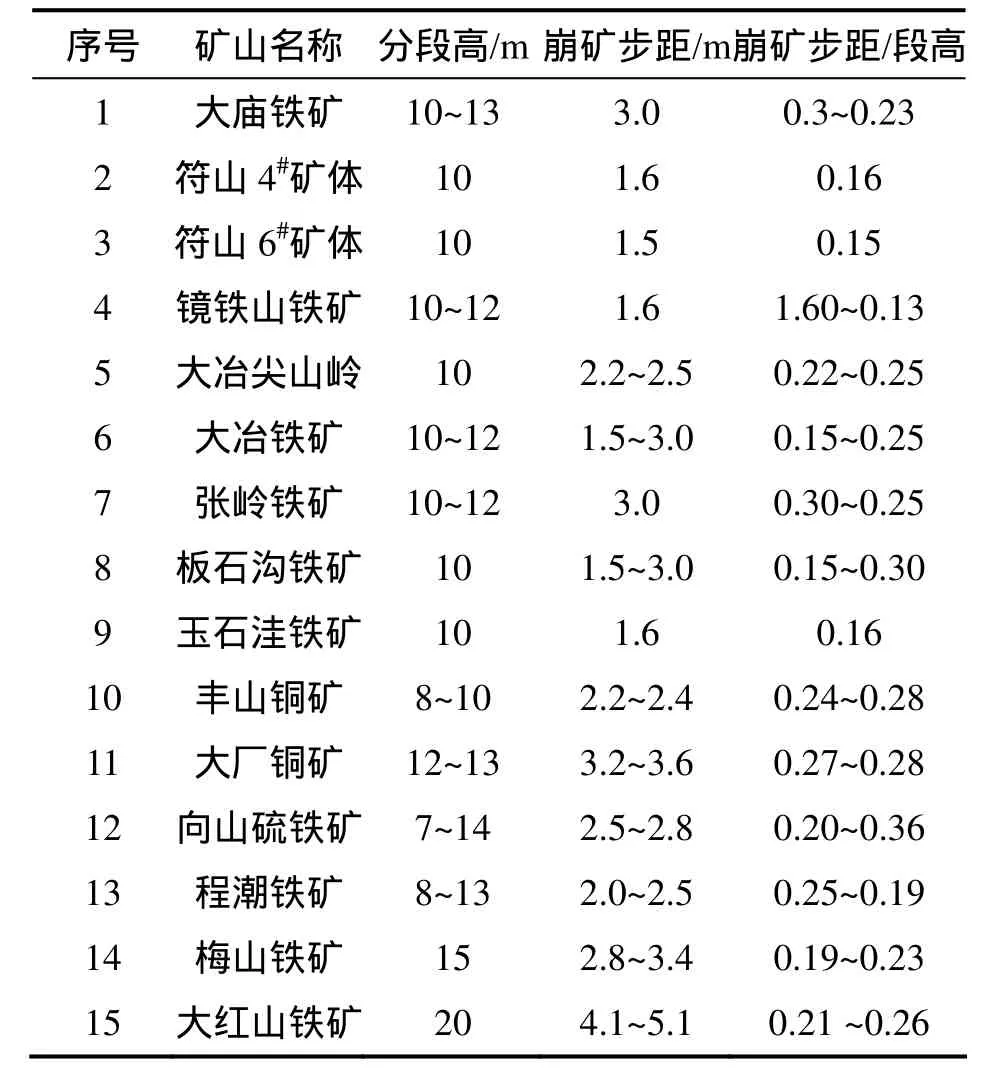
表2 国内部分矿山崩矿步距与分段高度的比例关系Table 2 Relationship between breaking interval and sublevel height of some domestic mines

按上述的比例关系，大红山铁矿的崩矿步距在2.14～6.00 m之间，理论计算的440 m分层的最优崩矿步距5.10 m和5.49 m都包含在上述范围内，说明这种估值方法是有一定依据的。

4 结论

（1） 对于投资者而言，经济效益的最大化才是最终目的。以单位工业储量盈利作为确定最优崩矿步距的目标函数，保障了矿床开采整体经济效益的最大化，这样确定的崩矿步距才更科学、更可靠。

（2） 随着市场矿石价格和精矿价格的波动、围岩品位的变化，求得的最优崩矿步距也会随之改变，但以此确定的企业最终盈利都是最大的。

（3） 以单位工业储量盈利作为目标函数确定的最优崩矿步距具有可操作性和准确性。

[1] 刘兴国. 放矿理论基础[M]. 北京： 冶金工业出版社, 1995： 3−6.

LIU Xingguo. Ore drawing theory[M]. Beijing： Metallurgical Industry Press, 1995： 3−6.

[2] 孙光华, 吕广忠. 我国无底柱分段崩落法的发展方向[J]. 河北理工学院学报, 2007, 29（2）： 4−6.

SUN Guanghua, LÜ Guangzhong. The development direction of no-pillar sublevel caving mining in China[J]. Journal of Institute of Technology, 2007, 29（2）： 4−6.

[3] 王文杰, 任凤玉. 无底柱分段崩落法矿石贫化原因分析[J].中国矿业, 2008, 17（3）： 69−72.

WANG Wenjie, REN Fengyu. The ore depletion reasons analysise of sub-level caving method[J]. China Mining Magazine, 2008, 17（3）： 69−72.

[4] Freidin A M, Neverov S A, Neverov A A, et al. Mine stability with application of sublevel caving schemes[J]. Journal of Mining Science, 2008, 44（1）： 82−91.

[5] Bull G, Page C H. Sublevel caving-today’s dependable low-cost‘ore factory’[C]//MassMin 2000 Proceedings. Brisbane： The Australasian Institute of Mining and Metalurgy, 2000： 537−556.

[6] 周传波. 无底柱分段崩落法崩矿步距及贫损指标的计算模型与实例[J]. 有色矿冶, 1994（4）： 5−8.

ZHOU Chuanbo. Sublevel caving method without sill pillar caving step distance and the dilution and loss index calculation model and instance[J]. Non-ferrous Mining and Metallurgy, 1994（4）： 5−8.

[7] Sen S K, Shaykhian G A. Matlab tutorial for scientific and engineering computations[J]. Nonlinear Analysis Theory Methods and Applications, 2009, 71（12）： 1005−1020.

[8] 余健, 刘培慧. 高分段大间距结构合理崩矿步距研究[J]. 矿业研究与开发, 2008, 28（6）： 10−12.

YU Jian, LIU Peihui. Study on reasonable caving space for pillarless sublevel caving with high sublevel and large drive interval[J]. Mining Research and Development, 2008, 28（6）： 10−12.

[9] 马志刚, 岳润芳, 任凤玉. 回收进路放矿规律及截止品位确定方法研究[J]. 矿业工程, 2003, 1（3）： 23−24.

MA Zhigang, YUE Runfang, REN Fengyu. Regular pattern of ore drawing in the case of recovery access and research of calculating cut-off grade of ore[J]. Mining Engineering, 2003, 1（3）： 23−24.

[10] 苏金明, 阮沈勇. MATLAB 6.1应用指南[M]. 北京： 电子工业出版社, 2002： 35−55.

SUN Jinming, RUAN Shenyong. MATLAB 6.1 Application Guide[M]. Beijing： Electronic Industry Press, 2002： 35−55.

[11] 陈兴发, 张志雄. 大参数无底柱分段崩落法在大红山铁矿的运用[J]. 有色金属设计, 2009, 36（3）： 18−21.

CHEN Xingfa, ZHANG Zhixiong. Application of big parameter of no-pillar sublevel caving in dahongshan iron mine[J]. Nonferrous Metals Design, 2009, 36（3）： 18−21.

（编辑 何运斌）

Optimization of breaking interval in non-pillar sublevel caving mining

WANG Yunpeng, YU Jian
（School of Resources & Safety Engineering, Central South University, Changsha 410083, China）

Considering that the ore drawing dilution rate is influenced by different combinations of sublevel height, drive interval and step of blasting, the method of structural parameter optimization and loss and dilution rate calculation formula were studied. After dilution rate was founded to confirm the step of blasting, the objective function of maximization of industrial unit of reserves gain and union of concentrate gain were established as mathematical model. The traditional method only considering loss and dilution rate to define structural parameter was changed. A new approach was created to define structural parameter for the purpose of gaining the maximal benefit in the deposit exploitation.

breaking interval; ore drawing; ore loss and dilution rate; economic benefit

TD853.36+2

A

1672−7207（2014）02−0603−06

2013−02−08；

2013−04−18

云南省省院省校科技合作计划重大资助项目（2003UDBEA01A052）

余健（1960−），男，重庆人，教授，从事无轨机械化采矿工艺与技术研究；电话：13974870542；E-mail：zxs143@163.com