沥青路面非线性疲劳损伤特性及应力状态演变规律

孙志林，卓斌，廖中平

（1. 长沙理工大学 道路灾变防治及交通安全教育部工程研究中心，湖南 长沙，410114；2. 湖南省高速公路管理局，湖南 长沙，410016）

沥青路面非线性疲劳损伤特性及应力状态演变规律

孙志林1，卓斌2，廖中平1

（1. 长沙理工大学 道路灾变防治及交通安全教育部工程研究中心，湖南 长沙，410114；2. 湖南省高速公路管理局，湖南 长沙，410016）

运用通用有限元软件ABAQUS及其二次开发平台，建立考虑路面材料非线性疲劳损伤的沥青路面结构数值计算模型，分析沥青路面结构在车辆荷载反复作用下路面结构损伤的空间分布、演化规律以及路面结构内部水平正应力的空间分布与演化规律。研究结果表明：路面结构损伤主要分布在双轮中心线下靠近基层与底基层层底的区域，随着荷载作用次数增加，基层层底与底基层层底损伤度均增加，且增加幅度逐渐增大；双轮中心线下靠近基层与底基层层底区域，考虑损伤的路面结构相比无损路面结构，层底水平拉应力均有所减小，且随荷载作用次数增加，水平拉应力逐渐减小，减小的幅度逐渐增大。研究结果可用于路面维修养护中路面破坏区域及程度的判断，以及路面设计研究中设计指标的确定。

道路工程；路面结构；损伤力学；疲劳损伤模型；有限元

沥青路面疲劳破坏机理是长期研究的热点，有关学者利用断裂力学、损伤力学、现象学等方法针对沥青路面疲劳破坏进行了大量研究[1−4]。目前，针对沥青路面结构疲劳损伤过程的研究特别是基于损伤力学－有限元全耦合方法对沥青路面结构在交通荷载作用下疲劳损伤过程的相关研究较少[5−6]。为了更准确地分析沥青路面结构疲劳损伤过程，了解沥青路面结构在交通荷载下力学状态变化规律，本文作者将运用损伤力学－有限元全耦合方法，基于ABAQUS[7]计算平台及相应疲劳损伤用户材料子程序UMAT，分析沥青路面结构在车辆荷载作用下路面结构损伤度及应力状态的演化规律[8−9]，以便为沥青路面结构设计、养护维修等提供依据。

1 疲劳损伤有限元方法

在疲劳损伤力学理论中，一个广泛应用的非线性损伤演化模型即为Chaboche模型，其损伤演化方程为[10]

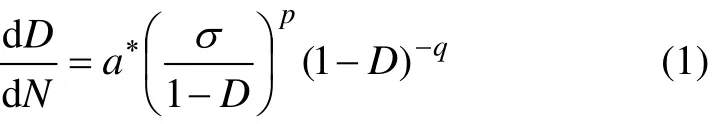
式中：D为损伤度，在本研究中取0≤D≤0.5；N为荷载作用次数（疲劳寿命）；a*，p和q为材料的疲劳损伤特性参数；σ为拉伸应力。本文采用此模型作为材料疲劳损伤分析模型。

有限元计算模型选择平面应变模型，此时，有限元方法的本构方程为

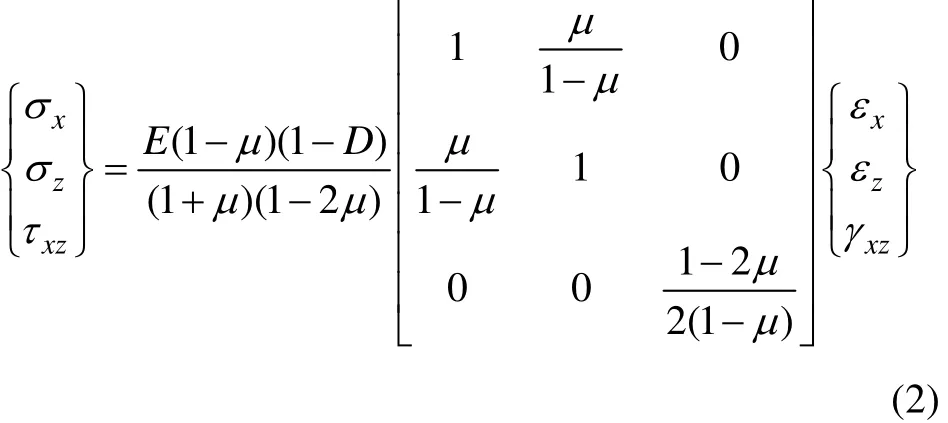
式中：σx和σz分别为x和z方向的正应力；τxz为剪应力；E为弹性模量；μ为泊松比；D为损伤度；εx和εz分别为x和z方向的正应变；γxz为剪应变。

为了准确地进行损伤力学有限元疲劳损伤累积分析，采用全耦合方法，即每隔一定的应力循环次数对单元刚度矩阵重新计算，以反映疲劳损伤累积效应对单元刚度矩阵的影响。在有限元软件ABAQUS提供的用户子程序接口上，采用FORTRAN77编写用户子程序UMAT，以反映疲劳损伤对单元刚度的影响，即耦合疲劳损伤的材料模型进行相应的编译连接，用于进行疲劳损伤分析。所用计算方法中，用户子程序UMAT中的单元刚度矩阵在每个增量步中都进行调用，每次调用之后按照疲劳损伤演化规律及时更新刚度矩阵中的疲劳损伤度D，因此，该方法属于全耦合解法，解法准确度要高于全解耦和半耦合解法，具有明确的物理意义。

2 结构计算模型

2.1 路面结构

采用我国目前常用的半刚性路面结构形式。路面结构各组成部分的材料如下：面层材料为沥青混凝土，基层材料为水泥稳定碎石，底基层材料为二灰土。各层材料的参数见表1。

表1 路面结构计算参数Table 1 Calculation parameters of pavement structure

有限元计算模型为平面应变模型，其长×宽为10 m×10 m。假定模型两侧与底部完全约束，路表为自由面，没有约束。靠近约束边界的位置各种力学响应很小，可忽略不计，故假定模型两侧与底部完全约束合理。

2.2 材料疲劳损伤参数

张行在有关拉伸疲劳试验中，针对Chaboche提出的模型，得出：

式中：KT为应力集中系数，在本文中取1；Ncr为裂缝形成疲劳寿命。

依据相关疲劳方程和试验数据[11−12]，可以得到p和c的值，并取q=0，由式（3）可计算出a*。整理计算结果如表2所示。

2.3 荷载条件

本文中，选取车辆荷载宽度W=156 mm，双轮中心距B=312 mm。选取荷载集度P=0.16 MPa，计算可得施加荷载为标准轴载，以保证各层结构的应力水平和路表弯沉在通常范围内，不影响路面结构力学响应的规律性分析。

表2 Chaboche疲劳损伤模型参数Table 2 Chaboche fatigue damage model parameters

3 损伤场分析

3.1 损伤度分布云图

图1所示为上述路面结构在车辆荷载作用600万次后，损伤度在路面结构中的分布云图。从图1可以看出面层没有损伤，基层与底基层均发生疲劳损伤，在双轮下靠近层底的位置损伤最严重。

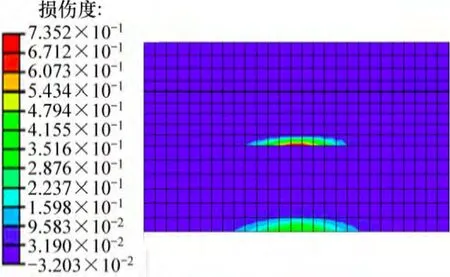
图1 损伤度分布云图Fig. 1 Cloud picture of damage degree distribution

3.2 损伤度空间分布规律

利用ABAQUS有限元计算软件，计算可得沥青路面结构在车辆荷载作用600万次后，损伤度空间分布规律如图2和图3所示，其中，图2所示为双轮中心线下垂直方向基层与底基层损伤度分布规律，图3所示为基层与底基层层底沿水平方向损伤度分布规律。

从图2可以看出：在双轮中心线下，无论是基层还是底基层，越靠近层底，损伤度越大，从层底往上损伤迅速减小；对于基层，距层底略5 cm处，损伤度已接近于0；对于底基层，损伤自下往上逐步递减，直到接近距层底约20 cm的位置损伤度接近0。可见底基层损伤范围比基层的要广，但损伤程度比基层的低。

图3所示为基层层底与底基层层底沿水平方向损伤度分布规律。从图3可以看出：损伤最大的位置出现在双轮中心线下，往两侧损伤度减小，说明该位置是整个结构最先出现破坏的地方；当损伤达到一定程度时，便会在此位置逐渐形成裂纹直至开展形成宏观裂缝；对于基层，距中心线25 cm的位置损伤度已经接近于0；对于底基层相对要缓慢点，不过在接近距中心线40 cm的位置损伤度也已经接近于0。该结果与损伤度云图反映的结果也一致。这种损伤区域集中的原因主要是非线形损伤模型中考虑了当前损伤度对损伤速率的影响。

图2 双轮中心线下基层与底基层损伤度Fig. 2 Damage degree of base and sub-base along middle line between double wheels

图3 基层与底基层层底损伤度Fig. 3 Damage degree at bottom of base and sub-base

3.3 结构层层底损伤度随荷载作用次数的变化

层底损伤度随荷载作用次数的变化规律如图4所示。从图4可以看出：基层层底的损伤度随着荷载作用次数的增加而增加；当荷载作用次数从0增加到50万次时，基层层底损伤度从0增加到0.018；当荷载作用次数从650万次增加到700万次时，损伤度增加了0.071；随着荷载作用次数的增加损伤度增加的幅度越来越快。底基层损伤度在初始阶段其增长速度比基层的小，但后期增长速度比基层的大。

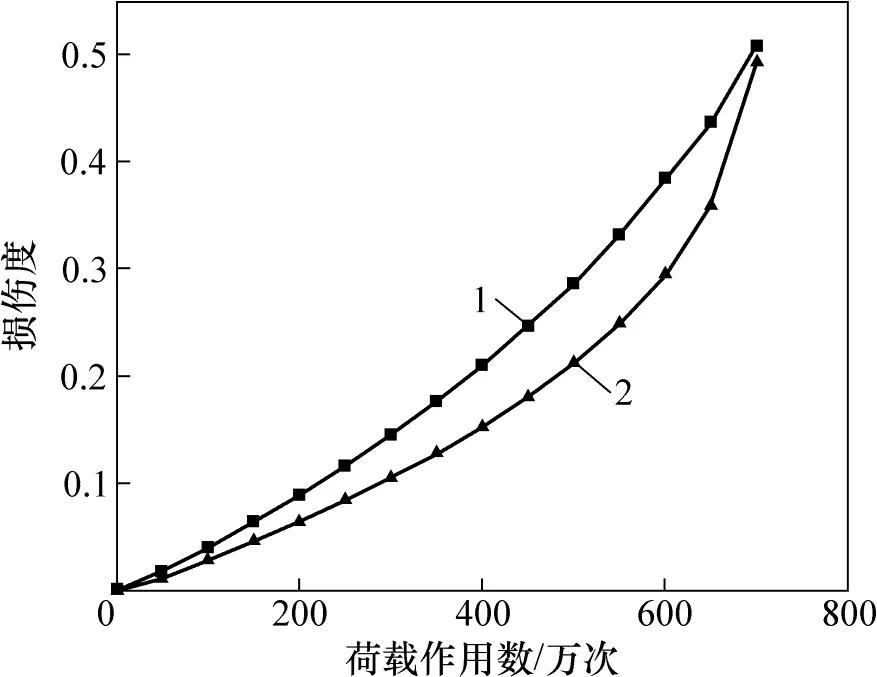
图4 层底损伤度随荷载作用次数的变化规律Fig. 4 Change law of damage degree at layer bottom with load cycles

选用Chaboche非线性疲劳损伤演化模型进行分析。该模型中损伤度演化率与当前损伤度有关，当前损伤度越大，损伤演化率越大；同时，随着损伤度的增大，分析点的水平拉应力会减小，有减小损伤演化率的趋势；当损伤度导致的损伤演化率增大值大于水平拉应力减小导致的损伤演化率减小值时，损伤度便会快速增大。

4 应力场分析

4.1 路面结构水平正应力空间分布规律

沥青路面结构在车辆荷载作用600万次后，基层和底基层双轮中心线下水平正应力和层底水平正应力分布规律分别如图5和图6所示。

从图5可以看出：双轮中心线下基层的水平正应力在整个厚度内不再呈线性分布；在靠近层底的一侧，由于受拉应力损伤的影响，与无损结构相比有所减小；但当距层底距离大于5 cm时，由于水平拉应力较小或者只有水平压应力，结构层的损伤很小或者没有，因此，水平拉应力保持线性变化。底基层内水平正应力在垂直方向的分布与基层的类似，在靠近层底的位置，由于受拉应力损伤的影响有所减小，当距底基层层底的距离大于7 cm以后则呈线性变化。但在底基层内水平正应力始终为拉应力。

从图6可以看出：基层层底水平正应力沿水平方向的分布呈现出下凹的应力分布图形。从双轮中心线的位置往两侧水平拉应力逐步增大，之后增大幅度有所减小，直到距中心线20 cm处水平拉应力不再增加，再往两侧水平拉应力开始减小，且减小的幅度很快增大；底基层水平正应力沿水平方向的分布与基层的类似，但底基层在中心线及其附近水平正应力减小幅度较大。

图5 双轮中心线下基层与底基层水平正应力Fig. 5 Horizontal normal stress of base and sub-base along middle line between double wheels

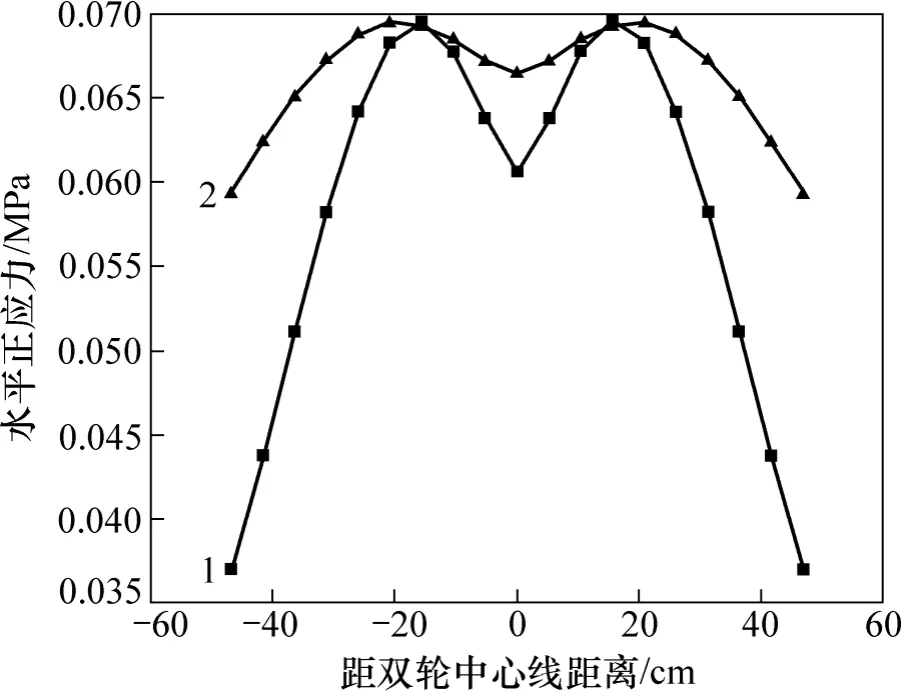
图6 基层与底基层层底水平正应力Fig. 6 Horizontal normal stress at bottom of base and sub-base

4.2 结构层层底水平正应力随荷载作用次数的变化

沥青路面结构双轮中心线下层底水平正应力随荷载作用次数的变化规律如图7所示。

从图7可以看出：随着荷载作用次数的增加，基层层底与底基层层底的水平正应力均减小，且减小的幅度逐步增大。这是因为随着荷载次数的增加，损伤减小的越来越快，损伤处模量的减小也会变快，由于应力的重分布作用，相应的水平正应力的减小也会逐渐加快。

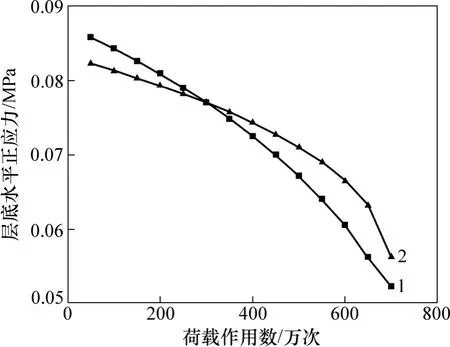
图7 层底水平正应力随荷载作用次数的变化规律Fig. 7 Change law of horizontal normal stress at layer bottom with load cycles

5 结论

（1） 路面结构的损伤主要分布在双轮中心线下靠近层底的区域；随着车辆荷载作用次数增加，基层层底与底基层层底的损伤度增加，且增长的幅度逐渐增大。依据结构损伤度的分析，可以实时了解结构在不同时期、不同位置损伤度的分布和损伤程度，从而确定对路面结构进行养护维修的时间和位置以及所采用的措施。

（2） 考虑损伤的路面结构相比不考虑损伤的路面结构，在双轮中心线下靠近层底的区域内，水平拉应力均有所减小；在双轮中心线下基层与底基层层底的位置，随着荷载作用次数增加，水平拉应力逐渐减小，且减小的幅度逐渐增大。路面结构层底应力水平并不是固定不变的，因此，有必要确定更合理的路面结构设计控制指标进行路面结构设计。

[1] Carpenter S H, Ghuzlan K, Shen S. Fatigue endurance limit for highway and airport pavements[J]. Transportation Research Record, 2003, 18（32）： 131−138.

[2] Castro M, Sanchez J A. Estimation of asphalt concrete fatigue curves： A damage theory approach[J]. Construction and Building Materials, 2008, 22（6）： 1232−1238.

[3] SI Zhiming, Little D N, Lytton R L. Characterization of microdamage and healing of asphalt concrete mixtures[J]. Journal of Materials in Civil Engineering, 2202, 14（6）： 461−470.

[4] 葛折圣, 黄晓明. 运用损伤力学理论预测沥青混合料的疲劳性能[J]. 交通运输工程学报, 2003, 3（1）： 40−42.

GE Zhesheng, HUANG Xiaoming. Prediction of asphalt mixtures fatigue properties using damage mechanics[J]. Journal of Traffic and Transportation Engineering, 2003, 3（1）： 40−42.

[5] SHU Xiang, HUANG Baoshan, Dragon V. Laboratory evaluation of fatigue characteristics of recycled asphalt mixture[J]. Construction and Building Materials, 2008, 22（7）： 1323−1330.

[6] 关宏信, 郑健龙, 张起森. 沥青混合料黏弹性疲劳损伤模型研究[J]. 力学与实践, 2007, 29（2）： 50−53.

GUAN Hongxin, ZHENG Jianlong, ZHANG Qisen. Viscoelastic fatigue damage model of bituminous mixture[J]. Mechanics in Engineering, 2007, 29（2）： 50−53.

[7] 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M].北京： 机械工业出版社, 2006： 23−36.

SHI Yiping, ZHOU Yurong. Detailed description of ABAQUS finite element analysis example[M]. Beijing： China Machine Press, 2006： 23−36.

[8] Tschegg E K, Jamek M, Lugmayr R. Fatigue crack growth in asphalt and asphalt-interfaces[J]. Engineering Fracture Mechanics, 2011,78（6）： 1598−1602.

[9] LI Qiang, Lee H J, Kim T W. A simple fatigue performance model of asphalt mixtures based on fracture energy[J]. Construction and Building Materials, 2012, 27（1）： 605−611.

[10] 郑健龙, 吕松涛. 沥青混合料非线性疲劳损伤模型[J].中国公路学报, 2009, 22（5）： 21−28.

ZHENG Jianlong, LÜ Songtao. Nonlinear fatigue damage model for asphalt mixtures[J]. China Journal of Highway and Transport, 2009, 22（5）： 21−28.

[11] 孙荣山, 汪水银. 级配变化对水泥稳定碎石材料疲劳性能影响的研究[J]. 公路交通科技, 2007, 24（6）： 57−61.

SUN Rongshan, WANG Shuiyin. Research on fatigue performance of the different gradation of cement stabilized crushed stone[J]. Journal of Highway and Transportation Research and Development, 2007, 24（6）： 57−61.

[12] 谢军, 郭忠印. 沥青混合料疲劳响应模型试验研究[J]. 公路交通科技, 2007, 24（5）： 21−25.

XIE Jun, GUO Zhongyin. Researching on fatigue model of asphalt mixtures[J]. Journal of Highway and Transportation Research and Development, 2007, 24（5）： 21−25.

（编辑 陈灿华）

Nonlinear fatigue damage characteristics and stress evolution law of asphalt pavement

SUN Zhilin1, ZHUO Bin2, LIAO Zhongping1

（1. Engineering Research Center of Catastrophic Prophylaxis and Treatment of Road & Traffic Safety, Changsha University of Science &Technology, Changsha 410114, China;

2. Hunan Expressway Administration Bureau, Changsha 410016, China）

Using general finite element software ABAQUS and the secondary development platform, an asphalt pavement numerical model which considers the pavement material nonlinear fatigue damage was established to analyze the asphalt pavement structure damage’s spatial distribution and evolution, the spatial distribution and evolution of the horizontal stress within the pavement structure. The results show that the pavement structural damage mainly distributes in a specific damage zone located at the bottom of the base and sub-base and along the middle line between the double wheels. With the increase of the load cycles, the damage degree at the bottom of the base and the sub-base increases, and the rate of which gradually increases. The horizontal tensile stress in the specific damage zone of a pavement structure considering damage is less than that of the pavement structure without considering damage. Simultaneously, this horizontal tensile stress gradually decreases, and the rate increases with the increase of load cycles. The results can be used to judge failure region and degree of the pavement structure on the asphalt pavement maintenance, and to determine the design index of the asphalt pavement design research.

road engineering; pavement structure; damage mechanics; fatigue damage model; finite element

U416.01

A

1672−7207（2014）02−0576−05

2013−05−25；

2013−09−10

国家自然科学青年基金资助项目（51008038，51208066）

孙志林（1979−），男，湖南慈利人，博士，讲师，从事路面工程研究；电话：15084967758；E-mail：sunzhilin1979@qq.com